Vektoren werden auf dieser Seite mit fetten Buchstaben in der Frakturschrift bezeichnet. Die Kodierung erfolgt mit Unicode-Glyphen 1D565 bis 1D59F. Diese werden mit aktuellen Versionen vieler Browser dargestellt. Nicht dargestellt werden sie mit Windows^® und iOS^® Versionen von Safari^®.

Drehbewegungen

Ein wichtiges Konzept, das Segler kennen sollten, ist die Physik der Drehbewegung. Sie ist die Grundlage zum Verstehen z.B. des Schraubeneffekts und der der Entstehung von Zyklonen (Tief­druck­ge­biete). Die physikalischen Größen sind der Bahndrehimpuls und das Drehmoment.

Der Bahndrehimpuls

Ein Körper — oder ein Massenpunkt, der sich auf einer gekrümmten Bahn bewegt, besitzt eine Ei­gen­schaft, die Bahndrehimpuls oder Drall genannt wird.

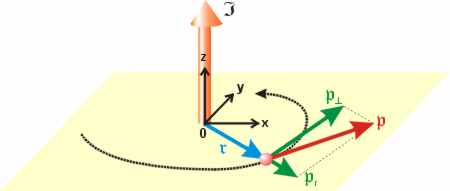
Der Körper bewege sich auf einer (Kreis-)Bahn mit dem Zentrum im Koordinatenursprung. Zu einem bestimmten Zeitpunkt hat der Massepunkt den (vektoriellen) Abstand 𝖗 vom Koordinatenursprung (Orts­vektor). Sein Impuls ist 𝖕 (die Frakturbuchstaben sympolisieren Vektoren, d.h. eine gerichtete Strecke mit den Parametern Länge und Richtung). Diesen Impuls der Bewegung zerlegt man in eine Kom­po­nen­te ent­lang des Ortsvektors 𝖕_𝖗 (radialer Impulskomponente) und eine senkrecht dazu 𝖕_⊥. Nur diese Kom­po­nen­te des Im­pul­ses des Massenpunktes geht in den Bahndrehimpuls ein; die radiale Komponente des Im­pul­ses hat kei­nen Einfluß auf den Bahn­dreh­im­puls. (Wenn er Impuls entlang des Ortsvektors wirkt, also keine Kom­po­nen­te senkrecht dazu hat, bewegt sich der Massenpunkt geradlinig.) Der Bahndrehimpuls 𝕴 des Massenpunktes ist nun das Vektorprodukt des Ortsvektors 𝖗 und des Impulses 𝖕:

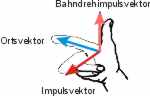Aus den Regeln der Vektorrechnung folgt, dass der Bahndrehimpuls senk­recht auf der Ebene steht, die vom Ortsvektor und dem Im­puls­vek­tor gebildet wird. Die Richtung des Bahndrehimpulsvektors ermittelt man mit Daumen, Zeige- und Mittelfinger der rechten Hand, die in die drei Raum­rich­tun­gen deuten: zeigt der Zeigefinger in Rich­tung des Orts­vek­tors, der Mittelfinger in Richtung der senkrechten Komponente des Impulsvektors, dann deutet der Daumen in Richtung des Bahndrehimpulses.

Die Länge des Bahndrehimpulsvektors |𝕵| (oder seinen Betrag) berechnet man aus dem Vektor-Produkt: |𝕵| = |𝖗| · |𝖕| · sin α. Dabei sind |𝖗| der Abstand zum Koordinatenursprung, |𝖕| der Betrag des Impulses (die Länge des Vektors), und α der Winkel zwischen Ortsvektor und Impulsvektor.

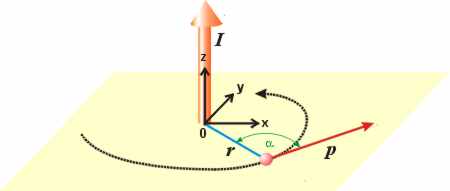
Der Impuls ist das Produkt aus (träger) Masse m und Geschwindigkeit 𝖛. Er hat also die Benennung (kg · m) ⁄ s; der Bahndrehimpuls hat daher die Benennung (kg · m²) ⁄ s.

Aus der Konstanz des Bahndrehimpulses folgt direkt das 2. Keplersche Gesetz. Der Ortsvektor ent­spricht dann der Ellipsenbahn. Die Formel für den Bahndrehimpuls (𝕴 = 𝖗 x 𝖛 · m) löst man nach der Ge­schwin­dig­keit auf, und erhält einen Ausdruck für die Umlaufgeschwindigkeit der Planeten in Ab­hän­gig­keit von ihrer Stellung.

Etwas einfacher [;-)] werden die Formeln, wenn sich der Massenpunkt auf einer Kreisbahn bewegt (dann ist der Impuls gleich der Komponente senkrecht zum Ortsvektor). Man kann dann die Bahn­ge­schwin­dig­keit durch das Vektorprodukt aus Winkelgeschwingigkeit ω (als Vektor) und Ortsvektor ersetzen:

Drehimpuls der Kreisbewegung

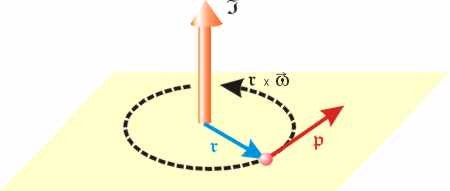
Die Richtung des Drehimpulses wird - wie die des Bahndrehimpulses - mit der rechten Hand ermittelt, ihre skalare Größe analog mit der Formel: I = m · r² · ^2·π/_t (dabei sind m die Masse des Punktes, r der Kreisradius und t die Zeit für einen vollständigen Umlauf; 2·π = 360°).

Das Produkt m · r² nennt man Trägheitsmoment der Kreisbewegung.