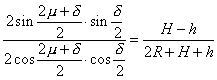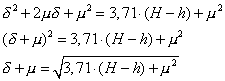Entfernungs- und Abstandsbestimmungen

Der Navigator kennt folgende Entfernungsbestimmungen:

1. mit Höhenwinkelmessung:
   • Entfernung zu einem Objekt bekannter Höhe,
   • Entfernung zu einem Objekt bekannter Höhe in der Kimm,
   • Entfernung zu einem Objekt bekannter Höhe teilweise hinter der Kimm,
   • Entfernung zur der Kimm,
   • "Kimmtiefe",
2. mit Horizontalwinkelmessung:
   • Entfernung zu einem Objekt durch Versegelung,
   • Entfernung zu einem Objekt durch Vierstrichpeilung und Verdoppelungspeilung.

Objekt bekannter Höhe teilweise hinter der Kimm

Ist es möglich, aus der bekannten Höhe eines Berges, der teilweise hinter der Kimm liegt, durch Messen des Winkels, unter dem man den sichtbaren Teil sieht, dessen Entfernung zu bestimmen? Im Admirality Manual of Navigation von 1955 fand ich einen Hinweis auf eine Tabelle (Lecky′s Tables), die einen Zu­sam­men­hang zwischen der beobachteten Höhe eines teilweise vom Horizont verdeckten Berges und sei­ner Entfernung angegeben hatte. Aber in einer neueren Ausgabe (1995) von Bowditch: The Practical American Navigator findet sich kein Hinweis mehr auf dieses Problem. Aber in der Ausgabe von 2002 ist die Tabelle wieder enthalten! Die Amerikaner hatten 1950 schon Computer, und konnten das Problem nummerisch lösen und eine Tabelle erstellen. Mich interessierte aber das trigonometrische Problem. Mehr als 2 Jahre nachdem ich es dargestellt hatte, erhielt ich von einem Besucher dieser Seite einen Ansatz zur Ableitung einer Formel. Kurz darauf hatte ich auch eine Kopie des "Lehrbuch der Navigation" 2. Auflage, herausgegeben vom Reichs-Marine-Amt im Jahre 1906, erhalten.

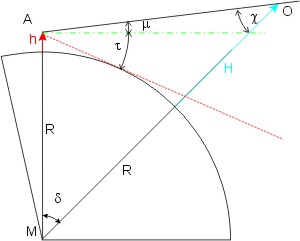Betrachten wir die Skizze die Skizze des Prob­lems: die waagrechte (Hilfs-)Linie (grün) geht vom Auge des Betrachters genau waage­recht auf den Berg zu. In der Skizze sind H die be­kann­te Höhe des Objektes, h die Au­ges­höhe, R der Erdradius, δ ist die Entfernung zum Objekt in Bogenminuten, τ die Kimmtiefe. Die Winkel μ und χ sind nur Hilfswinkel; sie kürzen sich in der arithmetischen For­mel­ar­beit wieder heraus. (Im Grunde sind sie dazu da, ein rechtwinkliges Dreieck zu erzeugen.)

Der Winkel ∠MAO = 90° + μ, der Winkel ∠AMO = δ, und der Winkel ∠AOM = χ = 
= 180° - ∠MAO - ∠AMO = 180° - 90° - μ - δ = 
= 90° - (μ + δ) (Winkelsumme im Dreieck!).

Jetzt wendet man den Sinussatz an:

Die Seiten eines schiefwinkligen Dreiecks verhalten sich wie die Sinuswerte der den Seiten gegenüberliegenden Winkel.

und erhält die Gleichung

für die beiden Seiten MA = R + h und MO = R + H. Und durch Umformen (Trennen der Winkelfunktionen) ergibt sich:

Nun folgt eine etwas unübersichtliche arithmetische Umformung (Additionstheoreme!) mit dem Ziel, die Sinus- und Cosinusfunktion in eine Tangensfunktion umzuwandeln. Die wesentlichen Schritte sind:

Schliesslich erhält man:

In dieser Formel kann man die Größe von H + h gegenüber 2 · R ohne großen Fehler vernachlässigen;, und da μ und δ naturgemäß klein sind, kann man ohne großen Fehler schreiben tan (μ + δ ⁄ 2) = (μ + δ ⁄ 2) · sin 1´ bzw. tan (δ ⁄ 2) = (δ ⁄ 2) · sin 1´. Man erhält also den vereinfachten Ausdruck:

Der wird wieder umgeformt (Division durch sin 1´·sin 1´, Multiplikation mit 2):

Der Bruch enthält nur Konstanten (R = 6.378.137 m) und kann als Faktor 3,71 angegeben werden. Gleichzeitig addiert man zu beiden Seiten der Gleichung μ²:

Da der gemessene Höhenwinkel α des Objektes sich als Summe darstellt, erhält man μ = α - τ. Diesen Ausdruck substituiert man und löst nach δ auf:

Mit dieser Formel berechnet man die Entfernung δ zum Objekt in Bogenminuten (= sm!) aus der be­kannten Höhe H (in Metern) des Objektes, dem gemessenen Höhenwinkel α (in Bogenminuten) und der Kimmtiefe τ (in Bogenminuten). Die Kimmtiefe in Abhängigkeit von der Augeshöhe (in Metern) entnimmt man einer Tabelle, oder man berechnet sie mit dem Rechenschieber.

Will man die Refraktion berücksichtigen, ändern sich die Faktoren in der Gleichung:

Da die Höhe eines Berges in Metern auf einer Insel i. d. R. vierstellige Zahl ist, die Augeshöhe aber ein- oder zweistellig, muss man mit 4 signifikanten Stellen rechnen. Das übersteigt die Rechen­schie­ber­ge­nauig­keit, und man rechnete (umständlich) mit der Logarithmentafel. Meist kann man aber nicht sicher sein, ob der Berg nun in der Kimm oder hinter ihr seinen Fuß hat. Also mißt man zunächst den Winkel α, und überschlägt die Entfernung mit der Formel für ein Objekt vor der Kimm: δ₁ = (13 ⁄ 7) · (H ⁄ α). Dann berechnet man die Kimmentfernung für die Augeshöhe h mit der Faustformel: δ₂ = 2,075 · √h. Ist δ₂ > δ₁, so liegt der Berg diesseits der Kimm, und man hat die Entfernung schon. Ist dagegen δ₂ < δ₁, suche man die Logarithmentafel …

Rechenbeispiel aus den Lehrbuch des Reichs-Marine-Amts

• (H - h) = 3.717 - 8,3 = 3.708,7
• α = 94,5′
• τ = 0,032 · √8,3. = 0,092° = 5,53′
• unter Berücksichtigung der Refraktion: τ = 5,5₃′ ⁄ 1,08 = 5,1₂′
• (α - τ) = 89,4′

Es muss also der Ausdruck δ = √[3,71 · 3.708,7 + (89,4′)²] - 89,4′ berechnet werden. Mit dem Taschen­rechner erhält man δ = 58,1′ = 58 sm. (Das Lehrbuch erhält mit der Logarithmentafel 60 sm.) Mit dem Rechenschieber (hier wird der UNIQUE-Navigator von Burns Snodgrass verwendet) — der ist ja jenseits seiner Rechengenauigkeit von 4 signifikanten Stellen — berechnet man zuerst die beiden Summanden unter der Wurzel:

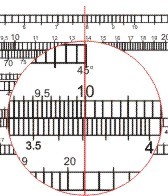
• (α - τ)²: man stellt auf der x-Skala B 894 ein und liest auf der x²-Skala 7995 ab, Ergebnis 7995

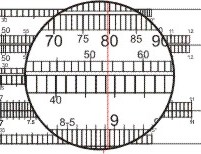
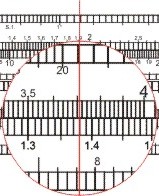
• [3,71 · 3.708,7: man schiebt die 10 auf der x-Zungenskala über 371 auf der x-Skala des Körpers und liest unter 3709 auf der Zunge auf dem Körper ab 1379, ergibt 13.790:

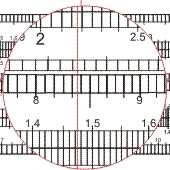• Die beiden Zahlen werden addiert: 21.785; diesen Wert auf der x²-Skala eingestellen und auf der x-Skala ablesen: 147,4.
• Hiervon noch (α - τ) = 89,4′ abgezogen, ergibt eine Entfernung vom 58′ (= sm).

Es ist wohl eher ein Zufall, dass der Rechenschieberwert und der Taschenrechnerwert gleich sind, sicher ist kein Beweis für die Ge­nauig­keit des Rechenschiebers.
Achtung: egal mit welchem Hilfs­mittel gerechnet wird: diese Ent­fer­nungs­"messung" ist eher eine Schätzung!

Quellen:

1. Squire Thornton Stratford Lecky: Wrinkles in Practical Navigation, London (1894).
2. Squire Thornton Stratford Lecky: The Danger Tables and Off-Shore Distance Tables. London (1882).
3. Lehrbuch der Navigation, Reichs-Marine-Amt (Herausg.), Berlin 1906.
4. Nathaniel Bowditch: The American Practical Navigator, Bethesda 2002.