Im rechtwinkligen Dreieck gibt es drei für die Navigation wichtige Sätze über die Verhältnisse der Seiten. Sie sind deshalb wichtig, weil man durch das Fällen einer Höhe jedes beliebige Dreieck in zwei rechtwinklige teilen kann. Die Höhe ist eine Strecke, die auf einer Seite senkrecht steht und durch die gegenüberliegende Ecke geht.
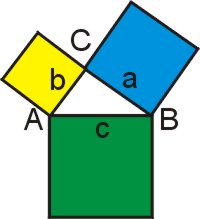
Der Satz des Pythagoras besagt, dass in einem rechtwinkligen Dreick die Summe der Quadrate der Kathetenlängen gleich der Summe des Quadrats der Hypotenusenlänge ist.
a2 + b2 = c2
Dieser Satz gibt den Einstieg in die Berechnung von beliebigen Dreiecken, wenn man die Länge zweier Seiten kennt. Mit dem Rechenschieber lassen sich diese Art Aufgaben schnell lösen.
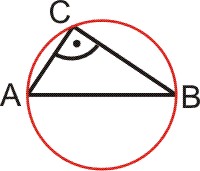
Ist AB der Durchmesser eines Kreises, so ist jedes Dreieck, dessen dritte Ecke auf dem Kreis liegt rechtwinklig.
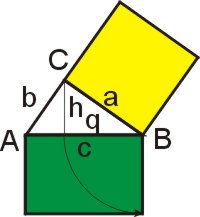
Euklid setzte die Hypotenuse des rechtwinkligen Dreiecks ins Verhältnis zur Kathete und dem Hypotenusenabschnitt, den die Höhe auf die Hypotenuse erzeugt. Das Quadrat der Kathete ist gleich dem Produkt aus Hypotenusenlänge und Länge des Hypotenusenabschnitts unter der Kathete.
a2 = c · q
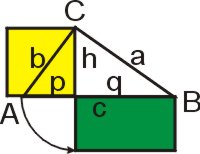
Dieser Satz im Zusammenhang mit dem Satz von Euklid ist wichtig, denn er gibt den Einstieg in die Sätze über Winkel im schiefwinkligen Dreieck.
Das Quadrat der Länge der Höhe h auf die Hypotenuse ist gleich dem Prokukt der beiden durch die Höhe erzeugten Hypotenusenabschnitten p und q.
h2 = p · q
Dieser Höhensatz ist eine Sonderform des Sehnensatzes. Der Kreis über AB als Durchmesser ist ein Thales-Kreis!
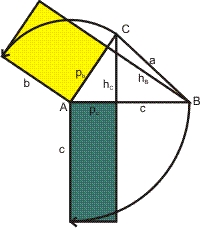
In einem beliebigen Dreieck sind die Rechtecke, die aus einer Seite und der orthogonalen Projektion der anderen gebildet werden, flächengleich.
c · pc = b · pb
Diesen Höhensatz kann man im allgemeinen, schiefwinkligen Dreieck formulieren. Er ist die Verallgemeinerung des Satzes des Euklids für das rechtwinklige Dreieck. (Systematisch passt er daher zu den hier aufgeführten Sätzen.)
c = pc + qc = a · cos β + b · cos α
Hieraus ergibt sich der Cosinussatz im schiefwinkligen Dreieck.
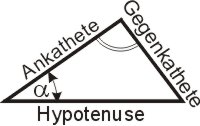
Das rechtwinklige Dreieck ist die Grundlage der ebenen und der sphärischen Trigonometrie. Da die Größe eines Winkels bekannt ist (der rechte hat 90°) und es den Satz des Pythagoras gibt, wird die Berechnung der anderen Größe leichter. Im Grunde löst man alle trigonometrischen Probleme, in dem man rechtwinklige Dreiecke sucht. Seine Seiten haben besondere Bezeichnungen: die dem rechten Winkel gegenüberliegende Seite heißt Hypotenuse, die beiden anderen Seiten, die den rechten Winkel einschließen, sind die Katheten. Am rechtwinkligen Dreieck werden auch die Winkelfunktionen definiert.
Die Definitionen der Winkelfunktionen erfolgt durch Seitenverhältnisse im rechtwinkligen Dreieck:
Damit kann man die vier Grundaufgaben der Berechnung aller Größen im Dreieck (3 Seiten und 3 Winkel) lösen, wenn man nur zwei zusätzlich kennt (das dritte, der rechte Winkel, hat definitionsgemäß 90°).
| gegeben ist die Hypotenuse c und ein anliegender Winkel α; |
|
| gegeben ist die Hypotenuse c und eine Kathete, z. B. a; |
|
|
|
|
| gegeben ist eine Kathete a und ein Winkel α; |
|
| gegeben sind die beiden Katheten a, b. |
|
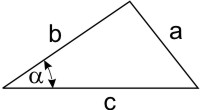
Es sind z. B. gegeben α und b. Aus den Definitionen der Winkelfunktionen:
Beide Gleichungen löst man nach c auf und erhält: a ⁄ sin α = b ⁄ cos α ⇒ a = b·(sin α ⁄ cos α) = b·tan α.
Damit kann man die Seite a berechnen. Die Seite c erhält man aus der Gleichung 2. Und der Winkel β ist β = 90° - α.
Analog kann man die anderen Grundprobleme nachvollziehen.
Gegeben sind die Kathete a und die Hypotenuse c.
Da Ingenieure häufig die Längen der Hypotenuse und einer Kathete kennen und die Länge der zweiten Kathete und die Winkel des Dreiecks wissen wollen, hat Alwin Oswald Walther an der TH Darmstadt 1934 die pythagoreische Skala mit Werten von √ 1 - x2) auf Rechenschiebern des System Darmstadt eingeführt.

Ein Rechenbeispiel ist im Abschnitt "Rechenschieber" ausgeführt.
© Dr. Rainer Stumpe, URL: https://www.rainerstumpe.de