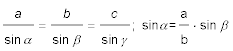Kursbestimmungen

Wenn man bei einem Törn weiss, wohin man will, bestimmt man zunächst den Kurs, mit dem man los­segeln will. Dabei unterscheidet man drei Berechnungsmethoden, die man je nach Entfernung vom Start- zum Zielort anwendet. Als nächstes interessiert bei der Törnplanung die Entfernung zwischen den beiden Orten. Die kann man aber in keinem der hier dargestellten Fälle aus der Karte ablesen: man muss immer rechnen.

1. Für kurze Entfernungen, d. h. wenn man die Erdoberfläche als eben annehmen kann, verwendet man die Methode der mittleren Breite. Diese Berechnung entspricht dem Ablesen des Winkels zwischen der Nordrichtung und der Verbindungslinie der beiden Orte auf der Seekarte. Die Mercator-Projektion ist ja winkelgetreu, aber nicht flächengetreu (damit kann man Entfernungen nicht direkt aus der Karte entnehmen, weil der horizontale Maßstab vom Cosinus der Breite anhängt).
2. Ist die Entfernung zu groß und muss man die Kugelgestalt der Erde berücksichtigen, rechnet man nach der Methode der Loxodrome. Die wird man anwenden, wenn Start- und Zielort nicht auf der gleichen Karte eingezeichnet sind.
3. Schließlich für sehr weite Entfernungen — wenn man über mehrere Zeitzonen den kürzesten Weg sucht — verwendet man die Methode der Orthodrome.

• Einfluß der Strömung,
• Einfluß der Bewegung des Ziels (Treffpunktproblem),
• Besteckversetzung,
• Einfluß des Windes.

Fahrt in der Strömung

Fährt man im Tidenrevier, wird man in aller Regel mit dem Tidenstrom konfrontiert. Da man die Strömung mit Bordmitteln nicht messen kann, entnimmt man ihre Richtung und Geschwindigkeit der Karte bzw. dem Gezeitenatlas. Da die Stromgeschwindigkeit abhängig ist vom Alter der Gezeit, muss man ein wenig rechnen oder einfach schätzen.

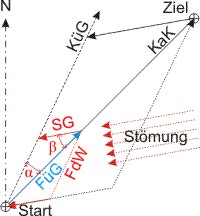Die nebenstehende Skizze stellt das Problem dar. Vom Startort zum Zielort entnimmt man den Kartenkurs KaK der Karte, oder berechnet ihn aus den Kartenkoordinaten der beiden Orte. Die Strömung — in der Skizze kommt sie schräg von vorn — be­ein­flusst nicht nur die Richtung (KüG), die das Boot tatsächlich nimmt, sondern auch seine wirkliche Geschwindigkeit (FüG). Um überhaupt am Zielort anzukommen, muss man also gegen die Strömung steuern. Die Kurskorrektur kann man natürlich be­rech­nen.

Die roten Pfeile im Parallelogramm mit der FüG auf der Ver­bin­dungs­linie Start-Ziel als Diagonale stellen die Ein­heits­vek­toren dar. Ihre Länge ent­spricht der Strecke, die das Boot in einer Stunde zurück legt. Wir erkennen ein Dreieck mit den bekannten Seiten FdW und Strom­ge­schwin­dig­keit, und dem bekannten Winkel der Strö­mungs­rich­tung β. Gesucht sind im Vektordreieck die Seite FüG und der Winkel α.

Die beiden kongruenten Dreiecke sind im allgemeinen schief­wink­lig, d. h. kein Winkel ist recht (= 90°), allerdings sind nicht alle Winkel notwendiger Weise spitz (< 90°). Man kann also zur Be­rech­nung prin­zi­piell den Sinussatz anwenden. Da der bekannte Winkel β der län­geren der beiden be­kann­ten Seiten Strom und FdW gegenüber liegt, handelt es sich um das dritte Grund­problem (es ist sicher anzunehmen, dass die Fahrt durch das Wasser schneller ist als die Strömungs­ge­schwindigkeit, also liegt β der längeren Seite gegenüber).

Die FüG ergibt sich nach dem Sinussatz mit dem Winkel γ, der sich aus der Winkelsumme im Dreieck und der Summe der beiden anderen Winkel ergibt: γ = 180° - (α + β). Da er i. d. R stumpf (γ gt; 90°) ist, nimmt man mit dem Rechenschieber den Supplementwinkel 180° - γ: γ = α  + β.

Zusammengefaßt verwendet man den Sinussatz in der Form:

Beispielrechnung

Ein Boot segelt mit FdW = 6 kn (FdW) den rwKaK = 45° durch einen Kanal zwischen 2 Inseln, in der ein Strom mit SG = 2,5 kn in rwRichtung 95° versetzt zu einem 30 sm entfernten Ort. Welchen Kurs muss das Boot zum Ziel steuern, und wie lange braucht es zum Ziel?

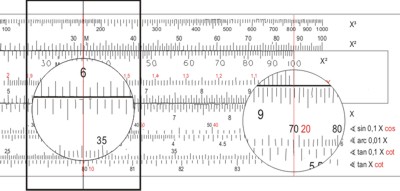
Besonders einfach ist die Rechnung mit einem Unique Navigator, der hat nämlich Sinus- und Tan­gens­skalen auf dem Körper und auf der Zunge. Man kann also durch Sinus bzw. Tangens dividieren. Man bildet also die Verhältnisse FdW ⁄ sin α = SG ⁄ sin α auf dem Rechenschieber ab:

1. Man stellt den sin β unter die FdW,
2. schiebt den Läufer auf die Strömungsgeschwindigkeit,
3. und liest auf der Sinuskala den Wert für α ab.

4. bewegt man den Läufer auf die Winkelsumme β + α  auf der Sinusskala und liest die FüG ab.

Man liest ab:

• α = 18,6°,
• WüG = 7,3.

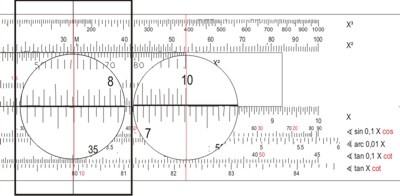
Etwas umständlicher ist die Rechnung mit einem gewöhnlichen Rechenschieber. Man muss die Glei­chun­gen des Sinussatzes umformen:

• 
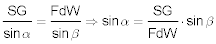
• Man stellt die "10" der C-Skala über "50°" auf der Sinusskala und schiebt den Läufer über "2,5" auf C.
• 
• unter den Läuferstrich schiebt man die "6" der Zunge, und liest unter "10" auf C den Winkel auf der Sinusskale ab: α = 18,6°.
• 

Zur Berechnung der FüG lösen wir den Sinussatz nach FüG auf:

• 
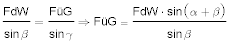
• Zuerst lesen wir den sin β = sin 50° = 0,766 auf dem Rechenschieber ab und notieren den Wert, dann stellen wir die "10" der Zungenskala C über 69° auf der Sinusskala und schieben den Läufer auf die "6" auf C
• 
• unter den Läuferstrich stellen wir 0,766 auf C und lesen auf D die FüG = 7,3 sm ab.
•