Der wahre und der scheinbare Wind
Berechnung des wahren Windes aus Kurs und scheinbarem Wind
Bereits im ersten Segelkurs lernt man, dass es drei Winde gibt: den wahren, den scheinbaren und den Fahrtwind. Gesegelt wird nach dem scheinbaren Wind — jedenfalls, was die Segelstellung angeht. In den Lehrbüchern findet man dann ein Diagramm und die Erklärung, der scheinbare Wind ergäbe sich durch Vektoraddition aus Fahrt- und wahrem Wind.
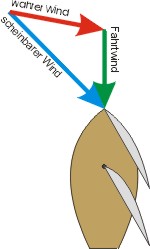
Der wahre Wind bläst aus einer Richtung mit einer Stärke, die man beim stillliegen beobachtet. Den Fahrtwind fühlt man, wenn man bei Flaute unter Motor fährt. Bewegt man sich in einem Windfeld, dann kann man die beiden „Winde“ nicht getrennt wahrnehmen: es ergibt sich der scheinbare Wind als Mischung der beiden vorgenannten Luftbewegungen.
Da „Wind“ beschrieben wird mit Richtung und Stärke, kann man ihn durch einen Pfeil symbolisieren: der Winkel zu einer vorgegebenen Referenzrichtung (beim Segeln die Nordrichtung) gibt die Windrichtung an (die Pfeilspitze zeigt in die Richtung, in die der Wind bläst!), die Länge des Pfeiles die Windstärke.
Solche Pfeile nennt man Vektoren, und man kann nach den Regeln der Vektoralgebra mit ihnen „rechnen“. Grafisch addiert man Vektoren, in dem man parallel verschiebt bis das Ende des einen mit der Spitze des anderen zusammenfält. Das Additionsergebnis ist dann der Pfeil vom Ende des zweiten zur Spitze des ersten Vektors. (Die nebenstehende Abbildung ist als Prinzipbild für die Vektorzerlegung gedacht; sie gibt nicht die wahren Verhältnisse wieder.)
Mit den Augen eines Trigonometriekenners sieht man ein schiefwinkliges Dreieck mit drei Seitenlängen (den Windstärken) und drei Winkeln (den relativen Windrichtungen). Man könnte also mit dem Rechenschieber rechnen (wenn ’mal die Windanlage an Bord ausgefallen ist).
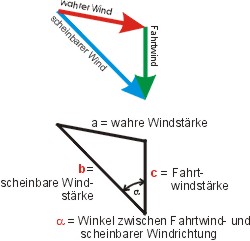
In dem Dreieck kennt man drei Stücke: den Winkel α (das ist die beobachtete Windrichtung relativ zur Bootsachse d. i. zum rechtweisenden Kurs rwK), die Stärke des Fahrtwindes (das ist die Geschwindigkeit im Wasser FdW) und die Stärke des scheinbaren Windes (die misst man mit dem Anemometer an Bord). Gesucht sind in der Regel Richtung und Stärke a des wahren Windes. Die Richtung (zu Nord) ergibt sich aus dem Winkel β, der ja der Kurswinkel rwK ist.
Wir kennen also zwei Seiten und den eingeschlossenen Winkel — eine typische Aufgabe für den Cosinussatz:
- a2 = b2 + c2 - 2·b·c·cos α
 Für den Rechenschieber einfacher wird die Rechnung, wenn man diese Formel umformt. Man ergänzt mit +2·b·c und -2·b·c und stellt etwas um:
Für den Rechenschieber einfacher wird die Rechnung, wenn man diese Formel umformt. Man ergänzt mit +2·b·c und -2·b·c und stellt etwas um:
- a2 = (b2 + 2·b·c + c2) - (2·b·c - 2·b·c·cos α) =
- = (b + c)2 - 2·b·c·(1 + cos α)
- a2 = (b + c)2 - 4·b·c·cos2(α ⁄ 2)
Mit dieser Formel muss man nur (b + c)2 und 4·b·c·cos2(α ⁄ 2) notieren. Den Winkel β zwischen Kurs rwK und wahrem Wind berechnet man mit dem Sinussatz (die Quotienten aus dem Sinus jeden Winkels und der gegenüberliegenden Seite sind gleich).
Beispielrechnung
Ein Boot segelt mit 6 kn auf Kurs rwK = 35°. Der scheinbare Wind weht mit 11 kn (4 Beaufort) aus 330°. Aus welcher Richtung und mit welcher Stärke bläst der wahre Wind?
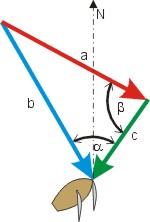 Der Winkel α beträgt α = (360° - 330°) + 35° = 65°. Mit α und den Seiten b (Stärke des scheinbaren Windes) und c (Stärke des Fahrtwindes) berechnen wir die Seitenlänge a, die die Stärke des wahren Windes repräsentiert.
Der Winkel α beträgt α = (360° - 330°) + 35° = 65°. Mit α und den Seiten b (Stärke des scheinbaren Windes) und c (Stärke des Fahrtwindes) berechnen wir die Seitenlänge a, die die Stärke des wahren Windes repräsentiert.
- a2 = (b + c)2 - 4·b·c·cos2(α ⁄ 2)
Der erste Term der Gleichung ergibt (b + c)2 = (11 + 6)2 = 172 = 289. Den cos(α ⁄ 2) = cos(65° ⁄ 2) = cos 32,5° = 0,84 quadrieren wir (= 0,71), multiplizieren mit 4 · 11 · 6 und erhalten 187,8. Die Differenz der beiden Terme ist a2 = 289 - 187,8 = 101,4; a = 10,1. ⇒ Der wahre Wind bläst mit 10 kn = 3 Bft.
Nach dem Sinussatz ist sin β = b ⁄ a · sin α = 11 ⁄ 10,1 · sin 65° = 0,987; β = 80°. Damit ist der Winkel γ zwischen scheinbarem und wahrem Wind 180° - 65° - 80° = 35°, und der wahre Wind kommt aus 330° - 35° = 295° (achterlicher als der scheinbare).
Berechnung von Richtung und Stärke des scheinbaren Windes aus Kurs und wahrem Wind
Interessanter könnte die Frage sein, mit welchem Kurs kann ich bei maximal möglicher Geschwindigkeit bei gegebener (wahrer) Windstärke und -richtung segeln? Die meisten Yachten fahren mit 80° bis 100° zum scheinbaren Wind am schnellsten. Die Frage bei der Törnplanung ist ja oft, wie steuere ich optimal, wenn das Ziel gegen den vorhergesagten Wind liegt?
Im Grunde ist das eine Optimierungsaufgabe. Man berechnet den Kurs bei einer Geschwindigkeit, die man erreichen mit 80° zum scheinbaren Wind erreichen kann. Stellt fest, wie weit man beim Kreuzen fahren muss und wie lange man zu dieser Strecke braucht. Im zweiten Schritt nimmt man den Kurs höher am Wind, und berechnet, wie lange man bei der dadurch reduzierten Geschwindigkeit brauchen wird. Nach ein paar Iterationen wird man einen optimalen Kurs gefunden haben.
Messung in der Praxis
Dieses Beispiel ist analog der Anleitung von Snodgrass "Wind and Drift Problems" gestaltet. Ein Besucher, Herr C. N., dieser Seite wies mich darauf hin, dass man bei einer Wende die Richtung des wahren Winds auf dem Kompass im den Augenblick ablesen kann, wenn der Wind genau von vorne kommt. Die Geschwindigkeit des wahren Winds erhält man aus der Differenz der Anzeigen von Logge und Anemometer.
|
|
© Rainer Stumpe URL: http://www.rainerstumpe.de |