Von der Kugel und dem Cylinder.
Zweites Buch

Satz 4

Eine gegebene Kugel durch eine Ebene dergestalt zu schneiden, dass die Oberflächen der Abschnitte in einem gegebenen Verhältnisse zu einander stehen.

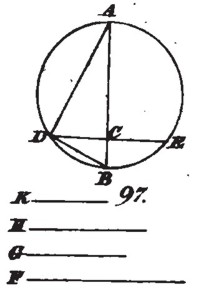
Diess sei geschehen: und es sei ADBE ein Normalkreis der Kugel, AB aber deren Durchmesser. Man erweitere eine auf AB senkrechte Ebene, welche den Kreis ADBE nach DE schneide, und ziehe AD, BD.

Weil also das Verhältniss der Oberfläche des Abschnitts DAE zur Oberfläche des Abschnitts DBE gegeben, der Oberfläche des Abschnitts DAE aber ein Kreis gleich ist, dessen Halbmesser = AD (I S. 49), und der Oberfläche des Abschnitts DBE ein Kreis, dessen Halbmesser = DB (I S. 48); weil ferner diese Kreise sich zu einander verhalten, wie AD² zu DB², d. h. wie AC zu CB, so ist das Verhältniss AC : CB das gegebene, und also der Punkt C ein gegebener. Auch steht AB senkrecht auf DE, also ist auch die durch DE gelegte Ebene der Lage nach gegeben.

Quelle: Ernst Nizze: Archimedes von Syrakus vorhanden Werke. Aus dem Griechischen. Verlag von Carl Löffler, Stralsund 1824.