Das Gnomon
In Johannes Keplers Liber Quintus stieß ich auf den Begriff "Gnomon". Kepler verwendet ihn in seiner Argumentation zu De figura orbitae. Er hat etwas mit algebraischer Geometrie zu tun. Aber was?
Euklid definiert das Gnomon im zweiten Buch seiner Elementa:
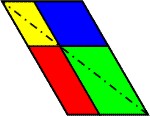
In der Fläche eines Parallelogramms wird jede ähnliche Parallelogrammteilfläche zusammen mit ihren Komplementen als Gnomon bezeichnet.Ähnlich sind die beiden Parallelogramme, die auf der Diagonalen liegen (gelb und grün). Die Komplenete sind rot und blau gefärbt. Das Gnomon ist also die Restfläche des Ursprungsparallelogramms ohne die gelbe Fläche.
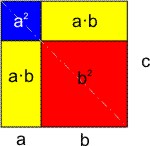Etwas hilfreicher — im Hinblick auf die algebraische Verwendung — ist es, wenn man ein spezielles Parallelogramm anschaut: das Quadrat mit der Seitenlänge c.
Wenn man nun ein Gnomon erstellt, sodass c = a + b, erkennt man unschwer für die Flächen die Gleichung a² + 2·a·b + b² = c².
- Helmuth Gericke, Mathematik in Antike und Orient, Springer-Verlag Heidelberg Berlin, 1984.
- David E. Joyce, Euclid's Elements, Math and Computer Science, Clark University, Worcester, MA, USA.
- Joh. Jos. Ign. Hoffmann: Die geometrischen Bücher der Elemente des Euclides; als Leitfaden zum Unterrichte in der Elementar-Geometrie, Mainz, 1829.
