Die Ellipse bei Apollonius von Perga

Die verschiedenen Parameter der Ellipse versteht man leichter, wenn man ihre Definition aus dem Werk "De Conicis" (Über die Kegelschnitte) von Apollonius von Perga anschaut. Apollonius lebte um 247 v. Chr. (ca. 262 bis ca. 190) und lebte überwiegend in Alexandia und Pergamon. Er verfasste ein acht Bücher über Kegelschnitte, deren Originale verloren sind. Sie lassen sich jedoch rekonstruieren aus den kommentierten Bearbeitungen arabischer (Thebit ben Corah, 830) und persischer (Abalphat von Ispahan (994), Nasireddin von Tus (1259)) Mathematiker. In Europa erkannte Regiomontanus (1436 bis 1476) die Bedeutung der Werke Apollonius und plante eine Übersetzung ins lateinische (zu der es nicht kam). Eine lateinische Ausgabe der ersten vier Bücher der "Conicis" erschien 1566 herausgegeben vom Venetianer Federicus Commandinus Urbinas (im Internet verfügbar) — gerade rechtzeitig für Johannes Keplers Astronomia Nova, der sich mit seiner Ableitung der Ellipsenbahn explizit auf Apollonius bezieht.

Da er in Alexandria mit Schülern des Euklid (um 300 v. Chr.) zusammen kam, bezog sich Apollonius auf dessen Definition im XI. Buch, Definition 18, des Kegels: "Wenn ein rechtwinkliges Dreieck um eine Kathete als Achse gedreht wird, beschreibt die Hypotenuse eine Kegeloberfläche (Mantel des Kegels)." In seinen Büchern zu Kegelschnitten untersucht Apollonius nun die Schnittlinien des Kegelmantels, wenn der durch verschieden geneigte Ebenen geschnitten wird. Er findet und benennt so die Parabel (Lehrsatz 11), die Hyperbel (Lehrsatz 12) und die Ellipse (Lehrsatz 13).

Diffinitiones Primæ

  1. Si ab aliquo puncto ad circumferentiam circuli, qui non sit in eodem plano, in quo punctum coniuncta recta linea in utranque partem producatur, & manete puncto convertatur circa circuli circumferentiam, quousque ad eum locum redeat, a quo cœpit moveri: superficiem a recta linea descriptam, constanteque ex duabus superficiebus, ad verticem inter sese aptatis, quarum utraque in infinitum augetur, nimirum recta linea, quæ eam describit, in infinitum producta, voco conicam superficiem.
  2. Verticem ipsius, manens punctum.
  3. Axem, rectam lineam, quæ punctum, & centrum circuli ducitur.
  4. Conum autem voco, figuram contentam circulo, & conica superficie, quæ inter verticem, & circuli circumferentiam interijcitur.
  5. Verticem coni, punctum, quod & superficiei conicæ vertex est.
  6. Axem, rectam lineam, quæ vertice ad circuli centrum perducitur.
  7. Basim, circulum ipsum.
  8. Conorum rectos quidem voco, qui axes habent ad rectos angulos ipsis basibus.
  9. Scalenos vero, qui non ad rectos angulos ipsis basibus axes habent.
  10. Omnis curvæ lineæ, in uno plano existentis, diametrum voco rectam lineam, quæ quidem ducta a linea curva, omnes lineas, quæ ipsa ducuntur, cuidam lineæ æquidistantes bifariam dividit.
  11. Verticem, lineæ terminum rectæ, qui est in ipsa linea.
  12. Ordinatim ad diametrum applicari dicitur, unaquæque linearum æquidistantium.
  13. Similiter & duarum curvarum linearum, in uno plano existentium, diametrum quidem transversam voco, rectam lineam, quæ omnes in utraque ipsarum ductas, lineæ cuidam æquidistantes bifariam dividit.
  14. Vertices linearum, diametri terminus, qui sunt in ipsis lineis.
  15. Rectam vero diametrum voco, quæ inter duas lineas posita, lineas omnes ductas, lineæ cuidam æquidistantes, & inter ipsas interiectas, bifariam secat.
  16. Coniugatas diametros voco curvæ lineæ, & duarum curvarum, rectas lineas, quarum utraque diameter est, & lineas alteri æquidistantes bifariam dividit.
  17. Axem vero curvæ lineæ, & duarum curvarum, rectam lineam, quæ cum sit diameter curvæ lineæ, vel duarum curvarum, æquidistantes ad rectos secat angulos.
  18. Axes coniugatos curvæ lineæ, & duarum curvarum, rectas lineas, quæ cum sint diametri coniugatæ, ipsis æquidistantes ad rectos angulos secant.

THEOREMA XIII. PROPOSITIO XIII.

Si conus plano per axem secetur, & secetur altero plano conveniente cum utroque latere tri­anguli per axem, quod neque basi coni æquidistet, neque subcontrarie ponatur; pla­num autem, in quo est basis coni, & secans planum conveniant secundum rectam line­am, quæ sit perpendicularis vel ad basim trianguli per axem, vel ad eam; quæ directum ipsi con­sti­tui­tur: recta linea, quæ a sectione coni ducitur æquidistans communi sectioni planorum usque ad diametrum sectionis, poterit spatium adiacens lineæ, ad quam sec­tio­nis dia­me­ter eam proportionem habeat, quam quadratum linea diametro æqui­dis­tan­tis a vertice coni usque ad trianguli basim ducta, habet ad rectangulum contentum basis partibus, quæ inter ipsam & rectas trianguli lineas intericiuntur; latitudinem habens li­neam, quæ dia­me­tro ab ipsa abscinditur ad verticem sectionis, deficiensque figura si­mi­li, & similiter posita ei, quæ diametro, & linea iuxta quam possunt, continetur di­ca­tur autem huiusmodi sectio ellipsis.

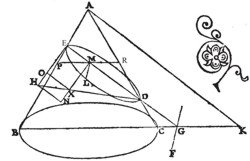
Sit conus cuius vertex A punctum, basis circulus BC; & secetur plano per axem, quod sectionem faciat triangulum ABC; secetur autem & altero plano, conveniente cum utroque latere trianguli per axem neque basi coni æquidistante, neque subcontrarie posito, quod faciat sectionem in superficie coni lineam DE; & communis sectio plani secantis, atque eius, in quo est basis coni, sit FG perpendicularis ad BC; diameter autem sectionis ED: & ab E ducatur EH ad ED perpendicularis; perque A ducta AK ipsi ED æquidisiante, fiat ut quadratum AK ad rectangulum BKC, ita DE ad EH; sumatur praeterea in sectione punctum L; & per L ipsi FG æquidistans ducatur LM. Dico LM posse spatium, quod lineæ EH adiacet, latitudinem habens EM, deficiensque figura simili ei, quæ DEH continetur.

Iungatur enim DH; perque M ducatur MXN æquidistans EH: & per H, X puncta ipsi EM æquidistates ducantur HN, XO; postremo per M ducatur PMR æquidistans BC. Itaque quoniam PR æquidistat BC; & LM ipsi FG: erit planum ductum per LM, PR æquidistans plano per FG, BC ducto, hoc est basi coni. si igitur planum per LM, PR producatur: fiet sectio circulus, cuius diameter PR. & est LM ad ipsam perpendicularis, ergo rectangulum BKC. Ita DE a EH: & proportion quadrati AK ad rectangulum BKC componatur ex proportione, quam habet AK ad FKB, & ex ea, quam AK habet ad KC, ut autem AK ad KB, ita EG ad GB, hoc est EM ad MP: & ut AK ad KC, ita DG ad GC, hoc est DM ad MR. erit proportio DE ad EH composita ex proportione EM ad MP, & ex proportione DM ad MR. sed proportio composita ex proportione EM ad MP, & DM ad MR est ea, quam EMD rectangulum habet ad rectangulum PMR.

Quare ut rectangulum EMD ad ipsum PMR, ita DE ad EH, videlicet DM ad MX. ut autem DM ad MX, sumpta ME communi altitudine, ita rectangulum DME ad rectangulum XME. ergo ut DME rectangulum ad rectangulum PMR, ita erit DME rectangulum ad ipsum XME. æquale igitur est rectangulum PMR rectangulo XME. sed rectangulum PMR demonstratum est æquale quadrato LM. quare & ipsum XME quadrato LM æquale erit. linea igitur LM potest spatitum MO: quod quidem linea EH adiacet, latitudinem habens EM, deficiensque figura ON simili ei, quæ DEH continetur. Vocetur autem huius modi sectio ellipsis: & linea EH, iuxta quam possunt, quæ ad diametrum DE ordinatim applicantur; quæ quidem & recta vocabitur ED vero transversa.

EVTOCIVS.

SCIRE oportet hoc theorema tres habere descriptiones, ut sapius dictum est in ellipsi: vel enim DE convenit cum latere AC supra C punctum, vel in ipso C, vel infra cum eo producto convenit.

FED. COMMANDINVS.

LINEA igitur LM potest spatium MO: quod quidem lineæ EH adiacet, latitudinem habens EM, deficiensque figura ON simili ei, quæ DEH continetur) Greca verba sunt hac. ἠ ΛΜ ἄρα δύναται τὸ ΜΟ, ὃ παράκειται παρὰ τινὶ θΕ πλάτος ἔχον τινὶ ΕΜ, ἐλλεῖπον εἴδει τῷ ΟΝ ὁμοίῳ ὄντι τῷ ὑπὸ ΔΕθ. Ex quibus manifeste constat, cur ea sectio ellipsis appelata sit.

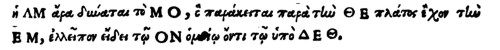Abbildung 2 Transscription mit freundlicher Hilfe von Walther Frederking — der außer Latein auch Griechisch kann.

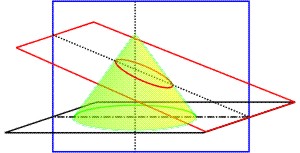Abbildung 1 Wenn ein (gerader Kreis-) Kegel (conus) durch eine Ebene, in der die Kegelachse liegt, geschnitten wird (plano per axem secetur), und durch eine andere Ebene geschnitten wird (secetur altero plano), die nicht parallel (eigentlich: gleiche Entfernung hat) zur Basis liegt (quod neque basi coni æquidistet), und mit den beiden Schenkeln des durch die erste Schnittebene gebildeten Dreiecks zusammentrifft (conveniente cum utroque latere tri­anguli per axem), und die nicht den gegenständigen Teil des Doppelkegels berührt (neque subcontrarie ponatur), die Ebene aber (pla­num autem), in der die Basis des Kegels liegt (pla­num autem, in quo est basis coni), in einer geraden Linie (& secans planum conveniant secundum rectam line­am) schneidet, die senkrecht steht sowohl auf der Basis(linie) des Dreiecks durch die Achse, als auch auf der schneidenden Ebene (quæ sit perpendicularis vel ad basim trianguli per axem, vel ad eam); diese gibt die Richtung vor (quæ directum ipsi con­sti­tui­tur): einer senkrechten Linie (recta linea), die vom Kegelschnitt parallel zur gemeinsamen Schnittlinie in der Schnittebene (quæ a sectione coni ducitur æquidistans communi sectioni planorum) bis zum Durchmesser des Schnitts gezogen wird (usque ad diametrum sectionis), diese wird eine Länge haben (poterit spatium adiacens lineæ), zu der der Durchmesser des Schnitts das gleiche Verhältnis hat (ad quam sec­tio­nis dia­me­ter eam proportionem habeat) wie das Quadrat einer Linie, die parallel zur Schnittebene von der Kegelspitze bis zu einem Schnittpunkt mit der verlängerten Basis des Dreiecks gezogen wird (quam quadratum linea diametro æqui­dis­tan­tis a vertice coni usque ad trianguli basim ducta), zum Rechteck aus der (verlängerten) Basis und dem Abschnitt der zwischen den Dreieckseiten liegt (ad rectangulum contentum basis partibus, quæ inter ipsam & rectas trianguli lineas intericiuntur); als Breite habe es [das Rechteck] eine Linie die vom Durchmesser abgeschnitten wird am Scheitel des Schnitts, und dem Rechteck fehlt ein Rechteck, das gleich ist und gleich dem gelegt sein kann, das vom Durchmesser und der verbundenen Linie, der so entstandene Kegelschnitt wird Ellipse genannt ( … dicatur autem huiusmodi sectio ellipsis).

Sei ein Kegel gegeben, dessen Spitze der Punkt A ist, mit einer kreisförmigen Basis BC; und werde er durch eine Ebene durch die Achse geschnitten, welcher Schnitt das Dreieck ABC erzeugt; und werde er außerdem durch eine andere Ebene geschnitten, die beide Seiten des Dreiecks durch die Achse treffen und weder zur Kegelbasis parallel sind, noch mit dem Gegenkegel zusammentrifft, was in der Ke­gel­ober­fläche eine Schnittline DE erzeuge; und der gemeinsame Schnitt der Ebene des Kegelschnitts mit der, in der die Basis des Kegels liegt, sei FG senkrecht zu BC; der Durchmesser des Kegelschnitts sei jetzt ED: und in E wird EH senkrecht zu ED gezogen; und AK von A parallel ED gezogen, so dass wie das Quadrat AK zum Rechteck BKC [sich verhält], so DE sich zu EH [verhält]; außerdem wird auf dem Ke­gel­schnitt ein Punkt L hinzugefügt; und von L die Strecke LM parallel zu FG gezogen. Ich behaupte LM hat eine Länge …

Erläuterungen

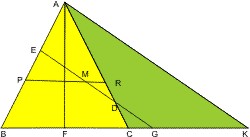Abbildung 3 In der Ebene durch die Kegelachse bilden die beiden Schnittlinien des Kegelmantels AB und AC ein gleich­sei­tiges Dreieck ABC (gelb), und die zur Kegel­schnitt­ebene EG parallele Linie AK ein stumpfwinkliges Drei­eck ACK (grün).

Durch die Konstruktion mit den parallelen Strecken EG und AK, die die Schenkel eines Winkels ∠ABK schnei­den, entstehen zwei ähnliche Dreiecke ABK und EBG. Es gilt für die Abschnitte auf den Schenkeln des Winkel ∠ABK: AB : BE = BK : BG. Also zusammengefaßt findet man die Verhältnisse

  • AK : EG = BK : BG = AB : BE.

Und die Strecke AK kann man mit dem Lehrsatz 12 aus dem zweiten Buch des Euklid mit der Kegelbasis ins Verhältnis setzen. In dem stumpfwinkliges Drei­eck ACK gilt:

"In einem stumpfwinkligen Drei­eck, ist das Quadrat der Seite, die dem stump­fen Winkel gegenüber liegt, größer als die Summe der Quadrate der bei­den Sei­ten, die den stump­fen Winkel einschließen, und zwar um das doppelte Rechteck aus einer der beiden Seiten und dem Abstand von der Dreiecksecke zum Fußpunkt F der Höhe AF."

Also:

  • AK2  = AC2 + CK2 + 2 · CF · CK = AC2 + CK2 + BC · CK 
  • (weil beim geraden Kreiskegel die Kegelachse jeden Durchmesser des Basiskreise halbiert:
  • 2 · CF = BC )

Es verhalten sich auch die Abschnitte auf den Schenkeln des Winkels ∠ABK, der durch die beiden Parallelen AK und EG geschnitten wird:

  • AB : BE = AK : EG
  • und
  • BK : BG = AK : EG
Valid HTML 4.01 © Rainer Stumpe URL: www.rainerstumpe.de