THEOREMA XIII. PROPOSITIO XIII.
Si conus plano per axem secetur, & secetur altero plano conveniente cum utroque latere trianguli per axem, quod neque basi coni aequidistet, neque subcontrarie ponatur; planum autem,in quo est basis coni, & secans planum conveniant secundum rectam lineam, quae sit perpendicularis vel ad basim trianguli per axem, vel ad eam; quae directum ipsi constituitur: recta linea; quae a sectione coni ducitur aequidistans communi sectioni planorum usque ad diametrum sectionis, poterit spatium adiacens lineae, ad quam sectionis diameter eam proportionem habeat, quam quadratum linea diametro aequidistantis a vertice coni usque ad trianguli basim ducta, habet ad rectangulum contentum basis partibus, quae inter ipsam & rectas trianguli lineas interijciuntur; latitudinem habens lineam, quea diametro ab ipsa abscinditur ad verticem sectionis, deficiensque figura simili, & similiter posita ei, quae diametro, & linea iuxta quam possunt, continetur dicatur autem huiusmodi sectio ellipsis.
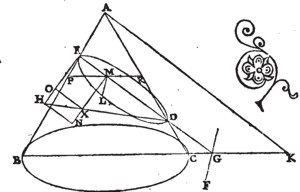
Sit conus cuius vertex A punctum, basis circulus BC; & secetur plano per axem, quod sectionem faciat triangulum ABC; secetur autem & altero plano, conveniente cum utroque latere trianguli per axem neque basi coni aequidistante, neque subcontrarie. posito, quod faciat sectionem in supcrficie coni lineam DE; & communis sectio plani secantis, atque eius, in quo est basis coni, sit FG perpendicularis ad BC; diameter autem sectionis ED: & ab E ducatur EH ad ED perpendicularis; perque A ducta AK ipsi ED aequidisiante, fiat ut quadratum AK ad rectangulum BKC, ita DE ad EH; sumatur praeterea in sectione punctum L; & per L ipsi FG aequidistans ducatur LM. Dico LM posse spatium, quod linea: EH adiacet, latitudinem habens EM, deficiensque figura simili ei, quae DBH continetur.
Iungatur enim DH; perque M ducatur MXN aequidistans EH: & per H, X puncta ipsi EM aequidistates ducantur HN, XO; postremo per M ducatur PMR aequidistans BC. Itaque quoniam PR aequidistat BC; & LM ipsi FG: erit planum ductum per LM, PR aequidistans plano per FG, BC ducto, hoc esi basi coni. si igitur planum per LM, PR producatur: fiet sectio circulus, cuius diametcr PR. & est LM ad ipsam perpendicularis, ergo rectangulum BKC. Ita DE a EH: & proportion quadrati AK ad rectangulum BKC componatur ex proportione, quam habet AK ad FKB, & ex ea, quam AK habet ad KC, ut autem AK ad KB, ita EG ad GB, hoc est EM ad MP: & ut AK ad KC, ita DG ad GC, hoc est DM ad MR. erit proportio DE ad EH composita ex proportione EM ad MP, & ex proportione DM ad MR. sed proportio composita ex proportione EM ad MP, & DM ad MR est ea, quam EMD rectangulum habet ad rectangulum PMR.
Quare ut rectangulum EMD ad ipsum PMR, ita DE ad EH, videlicet DM ad MX. ut autem DM ad MX, sumpta ME communi altitudine, ita rectangulum DME ad rectangulum XME. ergo ut DME rectangulum ad rectangulum PMR, ita erit DME rectangulum ad ipsum XME. aequale igitur est rectangulum PMR rectangulo XME. sed rectangulum PMR demonstratum est aequale quadrato LM. quare & ipsum XME quadrato LM aequale erit. linea igitur LM potest spatitum MO: quod quidem linea EH adiacet, latitudinem habens EM, deficiensque figura ON simili ei, quae DEH continetur. Vocetur autem huius modi sectio ellipsis: & linea EH, iuxta quam possunt, quae ad diametrum DE ordinatim applicantur; quae quidem & recta vocabitur ED vero transversa.