Drittes Buch des Apollonius von Perga über Kegelschnitte.

• 
  Lehrsatz 1. Wenn zwei Tangenten eines Kegelschnitts sich schneiden und die Durchmesser nach den Berührungspunkten gezogen und verlängert werden, so ist das Dreieck, dessen Ecken ein Berührungspunkt, der Durchschnitt des nach diesem gezogenen Durchmessers mit der zweiten Tangente und der Kreuzungspunkt der Tangenten sind, gleich dem andern ähnlich gebildeten Dreieck.
  
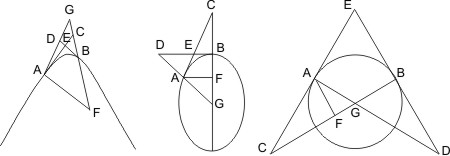
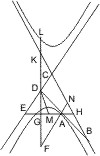
  Seien A, B zwei Punkte eines Kegelschnitts, in welchen Tangenten gezogen sind, die sich in F kreuzen, sei ferner D der Durchschnitt der Tangente in A mit dem nach B gezogenen Durchmesser und E der Durchschnitt der Tangente in B mit dem nach A gezogenen Durchmesser, so wird behauptet, dass ∆AEF = ∆DBF.
  Constr. Ziehe von B eine Parallele mit AD, bis sie EA in G trifft.
  Beweis.
  1. für die Parabel. Nach I. 35. ist EA = AG; da nun AG = BD, ist EA = BD, und da die Dreiecke AEF und BDF ausserdem noch gleiche Winkel haben, sind sie congruent, also auch gleich.
  2. für Ellipse und Hyperbel. Nach I. 37. ist CE : CA = CA : CG. Da nun CA : CG = CD : CB, ist auch CE : CA = CD : CB und folglich ∆CAD = ∆CBE, oder wenn man auf beide Seiten das Stück CEFD bei der Hyperbel und CAFB bei der Ellipse abzieht oder hinzufügt, so erhält man ∆AEF = ∆DBF. q. e. d.
  Anm. Bei der Ellipse sind in der Figur zwei Fälle zu unterscheiden, je nachdem die Punkte A und E, B und D auf derselben Seite des Mittelpunkts oder auf verschiedenen Seiten liegen.
• 
  Lehrsatz 2. Wenn ausser den im vorigen Lehrsatz angenommenen Linien noch von einem beliebigen Punkt des Kegelschnitts Parallelen mit den Tangenten gezogen werden, so ist das Viereck aus diesen beiden Parallelen, einer Tangente und dem nicht dazu gehörigen Durchmesser gleich dem Dreieck, das von derselben Tangente, dem dazu gehörigen Durchmesser und der Parallelen mit der andern Tangente gebildet ist.
  
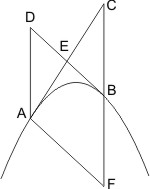
  Sei unter denselben Bezeichnungen wie im vorigen Lehrsatz G der auf dem Kegelschnitt angenommene Punkt und treffe die mit der Tangente in A gezogene Parallele die Tangente in B im Punkt H und den durch B gehenden Durchmesser in K, ferner die mit der Tangente in B gezogene Parallele die Durchmesser von A und B beziehlich in I und L, so wird behauptet, dass Viereck GHEI gleich Dreieck HBK ist.
  Beweis. Es ist in allen 6 Figuren bei der Parabel nach I. 42., bei Ellipse und Hyperbel nach I. 43. ∆GLK = BLIE. Subtrahirt oder addirt man nun auf beiden Seiten das Stück LBHG, so erhält man die Behauptung.
• 
  Lehrsatz 3. Wenn ausser den im Lehrsatz 1. angenommenen Linien von zwei beliebigen Punkten des Kegelschnitts Parallelen mit den Tangenten gezogen werden, so sind die Vierecke, welche von drei dieser Parallelen und je einem Durchmesser so gebildet werden, dass jedes an einen der beiden beliebig angenommenen Punkte anstösst, einander gleich.
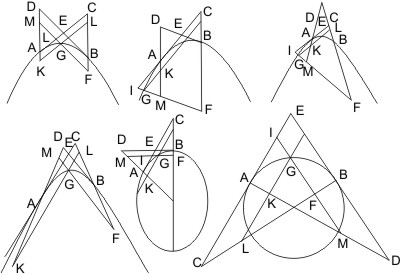
  Anm. Es lassen sich an jedem der beiden Punkte vier derartige Vierecke bilden, und da die Vierecke, die nach dem Lehrsatz gleich sein sollen, nicht beide an denselben Durchmesser anstossen, so bleiben für jedes an einem Punkt ansgewählte nur zwei an den andern Punkt anstossende zur Vergleichung, aus welchen das richtige leicht auszuwählen ist.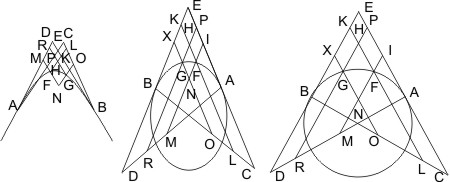
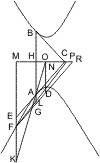
  Seien A und B wie früher die Punkte, durch welche Durchmesser und Tangenten gezogen sind, ferner C, D zwei beliebige Punkte, entweder beide zwischen A und B oder beide ausserhalb und auf derselben Seite angenommen; werden nun durch C und D Parallelen mit den Tangenten gezogen und schneidet die von C ausgehende mit der Tangente in B den Durchmesser von A in G, die von D ausgehende denselben in F, dagegen die von C ausgehende Parallele mit der Tangente in A den Durchmesser von B in H, die von D ausgehende denselben in I, ist ferner E der Kreuzungspunkt von CH mit DF, so ist zu beweisen, dass Viereck CEFG = Viereck DEHI.
  Beweis. Seien noch M, K und L die Durchschnittspunkte der Linien CG, DF und BH mit der Tangente in A, so ist nach vorigem Paragraph
  1. DILK = ∆AKF,
  2. CHLM = ∆AMG,
  woraus durch Subtraktion entsteht
  3. DIHE ± MKEC = ± FGMK oder DIHE = CEFG.
  Anm. 1. Die Bedeutung der Zeilen (1) und (2) ist in den beiden ersten Figuren einleuchtend, und bei Zeile (3) für diese nur zu unterscheiden, dass in der ersten das Minuszeichen, in der zweiten das Pluszeichen vor MKEC, während auf der andern Seite in beiden Fällen das Pluszeichen zu nehmen ist. In der dritten Figur sind die Vierecke DILK und CHLM sogenannte überschlagene Vierecke, deren Inhalt dem Unterschied der beiden Dreiecke, aus welchen sie bestehen, gleich zu setzen ist; auch kann über das Zeichen dieses Unterschiedes kein Zweifel sein, denn sei N der Durchschnittspunkt von CG mit BI, und denke man sich den Punkt C dem Punkte B nähern und ihn überschreiten, so wird dann das Viereck CHLM in ein einfaches übergehen, welches positiv zu nehmen ist, also ist CHLM = LMN - CNH und ebenso, wenn O der Kreuzungspunkt von DK und BI ist, DILK = LKO - DOI.
  Anm. 2. Es findet sich zu diesem Satz eine Anmerkung des Eutocius, dass die bei der Behauptung vorkommenden Vierecke nur dann entstehen, wenn die beiden Punkte C und D entweder beide zwischen A und B oder beide ausserhalb derselben angenommen werden; wenn aber einer von ihnen zwischen A und B und der andere ausserhalb angenommen wird, entständen die Vierecke nicht; dies ist jedoch nur so zu verstehen, dass in den erstgenannten Fällen die Vierecke einfache convexe Vierecke sind, im letzten Fall dagegen eins derselben ein überschlagenes Viereck ist; wie man sich durch Zeichnung einer Figur leicht überzengen kann.
• 
  Lehrsatz 4.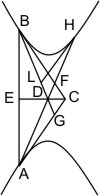 Wenn an jeden von zwei Gegenschnitten eine Tangente gezogen wird, so dass diese Tangenten sich schneiden, und wenn die beiden Durchmesser nach den Berührungspunkten gezogen und über den Mittelpunkt verlängert werden, so ist das Dreieck, dessen Ecken ein Berührungspunkt, der Kreuzungspunkt der Tangenten und der Durchschnitt des von diesem Berührungspunkt ausgehenden Durchmessers mit der am andern gezogenen Tangente sind, gleich dem andern ähnlich gebildeten Dreieck.
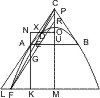
  Seien in den Punkten A und B zweier Gegenschnitte Tangenten gezogen, die sich in F kreuzen, ferner in A der Durchmesser AC, der BF in E, und in B der Durchmesser BC, der AF in D schneidet, so wird behauptet, dass ∆AFE = ∆BFD ist.
  Man ziehe in dem Punkt G, wo der Durchmesser AC den Gegenschnitt trifft, die Tangente, welche BC in H schneidet, so ist ∆ACD congruent ∆ CGH, aber ∆CGH nach § 1 gleich ∆CBE, folglich, wenn man zu den gleichen Dreiecken ACD und CBE das Stück CDFE hinzufügt, ∆AFE = ∆BFD.
• 
  Lehrsatz 5. Wenn zwei je an einen Gegenschnitt gezogene Tangenten sich schneiden und von einem beliebigen Punkt eines der beiden Gegenschnitte zwei Linien gezogen werden, eine parallel der Tangente an diesem Gegenschnitt und die andere parallel der Berührungssehne, so ist das von diesen beiden. Parallelen und dem nach dem Kreuzungspunkt der Tangenten gezogenen Durch­messer gebildete Dreieck vermindert um das ihm ähnliche Dreieck, das am Kreuzungspunkt entsteht, gleich dem Dreieck, das die mit der Berührungssehne gezogene Parallele mit der vorerwähnten Tangente und dem Durchmesser nach ihrem Berührungspunkt bildet.
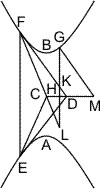  Seien in den Punkten A und B zweier Gegenschnitte Tangenten gezogen, die sich in D kreuzen, und von einem beliebigen Punkt E eines der beiden Gegenschnitte an den Durchmesser CD die beiden Linien EG ∥ AD und EF ∥ AB gezogen, sei ferner H der Punkt, in welchem die Tangente, und I der, in welchem der Durchmesser AC die Linie EF schneidet, so wird behauptet: ∆EFG - ∆HFD = ∆AHI.
  Beweis. Nach I. 45 ist ∆EFG = ∆CFI + ∆ACD, und subtrahirt man auf beiden Seiten ∆HFD, so erhält man ∆EFG - ∆HFD = ∆CFI + ∆ACD - ∆HFD = ∆AHI. q. e. d.
  Anm. Es mag noch derselbe Satz einer einfachen Hyperbel bewiesen werden. Seien also in den Punkten A und B einer solchen Tangenten die sich in D kreuzen, und von einem andern beliebigen Punkt E EF parallel AB und EG parallel AD bis an den Durchmesser CD gezogen, seien ferner H und I die Punkte, in welchen EF die Linien AD und AC schneidet, so ist zu beweisen, dass ∆FDH - ∆FGE = ∆AHI.
  Zieht man noch im Scheitel X die Tangente XY bis an den Durchmesser CA, so ist nach III § 1 ∆CXY = ∆CDA und nach I § 43 ∆EFG = XYIF, also:
  • CGEI = ∆CFI - ∆CFE = ∆CFI - FXYI = ∆CXY = ∆CDA,
  und subtrahirt man von CGEI = ∆CDA das gemeinsame CDHI, so bleibt DGEH = ∆AHI oder ∆FDH - ∆FGE = ∆AHI. q. e. d.
• 
  Lehrsatz 6. Wenn an zwei Gegenschnitten zwei sich schneidende Tangenten und die Durch­messer nach ihren Berührungspunkten, ferner von einem beliebigen Punkt eines der beiden Gegenschnitte Parallelen mit den Tangenten gezogen werden, so ist das Viereck zwischen diesen beiden Parallelen, einer Tangente und dem nicht zu ihr gehörigen Durchmesser gleich dem Dreieck, das an derselben Tangente und dem zu ihr gehörigen Durchmesser durch eine jener Parallelen abgeschnitten wird.
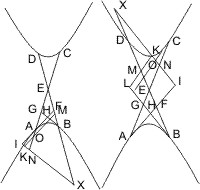  Seien A und B die Punkte, in welchen die Tangenten AI und BY und die Durchmesser AD, BE gezogen sind, F ein beliebiger Punkt eines der beiden Gegenschnitte und FG ∥ BY, bis es AI in G trifft, FH ∥ AI, bis es BE in H trifft, gezogen, sei ferner K der Durchschnittspunkt von AD und FG, so wird behauptet, dass FHIG = ∆AKG.
  Ist X der Schneidungspunkt von FG und BC, so kann man die Behauptung auch schreiben:
  • ∆IGX - ∆FHX = ∆AKG.
  Beweis. Man ziehe noch in D die Tangente, die FG in M, BE in L schneidet; ist nun Y noch der Schneidungspunkt der Tangente in B mit AD, so ist nach I. 44 und III. 1:
  • ∆FXH = ∆CXK - ∆CBY = ∆CXK - ∆CAI,
  • also
  • ∆CAl = ∆XK - ∆FXH
  und fügt man auf beiden Seiten das Viereck CKGI hinzu, so ist
  • ∆AKG = ∆XIG -∆XHF. q. e. d.
• 
  Lehrsatz 7. Wenn in zwei beliebigen Punkten zweier Gegenschnitte (die nicht Endpunkte eines Durchmessers sind) Tangenten und Durchmesser und von zwei andern beliebigen Punkten Parallelen mit den Tangenten gezogen werden, welche sowohl den Durchmessern als je einer Tangente begegnen, so sind zwei Vierecke, deren jedes aus drei dieser Parallelen und einem Durchmesser gebildet wird, so dass es an einen der zuletzt angenommenen Punkte anstösst, einander gleich.
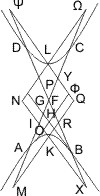  Anm. Dieser Satz, welcher eine Ausdehnung des § 3 auf Gegenschnitte ist, wird für mehrere Fälle besonders bewiesen, nämlich
  1. wenn die beiden zuletzt angenommenen Punkte in den Theilen der Gegenschnitte zwischen den zuerst angenommenen Punkten und zwischen den Endpunkten der von ihnen ausgehenden Durchmesser liegen, im vorliegenden § 7.
  2. wenn einer der Punkte zwischen den Endpunkten der Durchmesser liegt und der andere ein solcher Endpunkt selbst ist, im § 9.
  3. der Fall, in welchem beide Punkte Endpunkte der Durchmesser sind, führt zurück auf Lehrsatz, doch ist für diesen Fall im § 8 die Gleichheit zweier andern Vierecke bewiesen.
  4. der Fall, in welchem die beiden Punkte ausserhalb der zuerst angenommenen Punkte und der Endpunkte der von ihnen ausgebenden Durchmesser liegen, in § 10.
  5. der Fall, dass einer der Punkte zwischen den zuerst angenommenen Punkten , der andere ausserhalb der Endpunkte der von diesen ausgehenden Durchmesser liegt, kann gleichfalls leicht erwiesen werden.
  Seien in den Punkten A und B eines von zwei Gegenschnitten Tangenten und Durchmesser AD, BE gezogen, und von zwei andem Punkten F und G, deren einer auf der einen Hyperbel zwischen A und B, der andere auf der andern zwischen D und E liegt, Parallelen mit den Tangenten, welche einander in den Punkten H und X, den Durchmessern in den Punkten I, M, K, L begegnen, so wird behauptet
  • FIKH = GLMH oder FXLM = GXJK.
  Beweis. Seien N, O, P die Punkte, in welchen BC, FI, GH die Tangente in A schneiden. Nun ist nach vorigem Satz: 1) ∆AKP = LGPN und nach § 2 ∆AIO= FONM; setzt man also in (1) statt des Stückes AIO das ihm gleiche Viereck, so ist das Vieleck IKPNMF =LGPN, und fügt man hierzu noch das Stück NMHP, so erhält man FIKH = GLMH. q. e. d.
• 
  Lehrsatz 8. Wenn in zwei Punkten A und B eines von zwei Gegenschnitten Tangenten und Durchmesser und in den beiden andern Endpunkten dieser Durchmesser Parallelen mit den Tangenten gezogen werden, so sind die Vierecke, welche diese Parallelen mit je einer Tangente und dem nicht dazu gehörigen Durchmesser bilden, einander gleich.
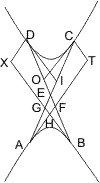  Seien in den Punkten A und B eines von zwei Gegenschnitten die Durchmesser AD und BE und die Tangenten und in den Punkten D, E Parallelen mit den Tangenten gezogen, welche mit je einer Tangente und dem nicht dazu gehörigen Durchmesser die Vierecke EFGH und DIKL bilden, so wird behauptet, dass DIKL = EFGH.
  Seien in den Punkten A und B eines von zwei Gegenschnitten die Durchmesser AD und BE und die Tangenten und in den Punkten D, E Parallelen mit den Tangenten gezogen, welche mit je einer Tangente und dem nicht dazu gehörigen Durchmesser die Vierecke EFGH und DIKL bilden, so wird behauptet, dass DIKL = EFGH.
  Sei M der Kreuzungspunkt der Tangenten in A und B, und GK und AB gezogen, so ist nach III. 1 ∆AMG = ∆BMK, und addirt man hierzu ∆GMK, so ist ∆AGK = ∆BGK, also AB parallel GK und CG : CA = CK : CB, also auch 2 · CA : CA - CG = 2 · CB : CB - CK, d. h. AD : AG = BE : BK, aber wegen Aehnlichkeit der Dreiecke AGM und ADL und BKM und BEH verhält sich ∆ADL : ∆AGM = AD² : AGsup>2 und ∆BEH : ∆BKM = BE² : BK², also auch ∆ADL : ∆AGM = ∆BEH : ∆BKM und da ∆AGM = ∆BKM, ist auch ∆ADL = ∆BEH, also, wenn man ∆ACK = ∆BCG subtrahirt, DCKL = ECGH und addirt man hierzu ∆DCI = ∆ECF, so erhält man DIKL = EFGH. q. e. d.
• 
  Besonderer Fall zu Lehrsatz 7. Wenn in zwei Punkten A und B eines von zwei Gegenschnitten Tangenten und Durchmesser AD, BE, von einem Punkt F des andern Gegenschnitts zwischen D und E Parallelen FG, FH mit den Tangenten in B und A bis an die Durchmesser AC, BC, endlich im Endpunkt D Parallelen DKI und DL mit den Tangenten in A und B gezogen werden, so ist zu beweisen, dass 1) ∆DIC = FHCG und 2) DLFG = HLDI.
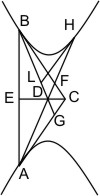  Beweis. Es ist nach III. 2 ∆DKG = FHIK und fügt man hierzu noch KICG, so ist ∆DIC = FHCG; fügt man aber FKDL hinzu, so ist DLFG = HLDI. q. e. d.
• 
  Besonderer Fall zu Lehrsatz 7. Seien in den Punkten A und B eines von zwei Gegenschnitten Tangenten und Durchmesser AD, BE und von zwei andern Punkten F in der einen Hyperbel ausserhalb AB und G in der andern ausserhalb DE Parallelen FM, FI, GL, GK mit den Tangenten bis an die nicht zu diesen Tangenten gehörigen Durchmesser gezogen. Sind H und X die Punkte, in denen sich diese Parallelen kreuzen, so ist zu beweisen, dass
  1. FHKI = GHML
  oder die überschlagenen Vierecke FXLM und GXIK einander gleich sind, d. h. wenn S und Z die Kreuzungspunkte von GL, AC und von FI, BC sind:
  2. ∆LZX - ∆FZM = ∆ISX - ∆GSK.
  Beweis zu Th. 1. Seien noch N, O, P die Punkte, in welchen die Tangente in A die Linien CB, FI, GH durchschneidet, und DY die Tangente in D bis an den Durchmesser BE, BT die in B bis an den Durchmesser CA.
  Nun ist nach I. 44.
  1. ∆GKS = ∆CLS - ∆CAN, und da ∆CBT = ∆CAN
  2. ∆CIZ - ∆CAN = ∆FZM, dies addirt giebt:
  3. ∆GKS + ∆CIZ = ∆CLS + ∆FZM,
  und fügt man hierzu das Stück GSCZFH auf beiden Seiten zu, so erhält man FHKI = GHML. q. e. d.
  Subtrahirt man Zeile 3) von XSCZ = XSCZ, so erhält man ∆XIS - ∆GKS = ∆XLZ - ∆FZM, welches die zweite Thesis ist.
• 
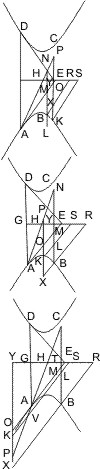  Lehrsatz 12. Wenn in zwei Punkten je eines Gegenschnitts (die nicht Endpunkte eines Durchmessers sind) Tangenten und zwei Durchmesser, deren einer von einem Berührungspunkt, der andere von der Mitte der Berührungssehne ausgeht, und ferner von zwei Punkten derjenigen Hyperbel, von welcher aus der eine Durchmesser gezogen ist, Parallelen mit der Tangente an dieser Hyperbel und mit der Berührungssehne gezogen werden, so sind zwei Vierecke, welche von drei dieser Linien und je einem der Durchmesser gebildet werden, und deren jedes an einen der angenommenen Punkte anstösst, einander gleich.
  Seien A und B zwei Punkte zweier Gegenschnitte, AD und BD die Tangenten in ihnen, E die Mitte ihrer Verbindungslinie, seien ferner von zwei Punkten F, G des Gegenschnitts A die Parallelen FL, GM mit der Tangente in A bis an den Durchmesser ED und die Parallelen FH, GI mit AB bis an den Durchmesser AC gezogen, welche AD beziehlich in N,O schneiden. Ist nun K der Kreuzungspunkt von FL und GI, so ist zu beweisen
  • FHIK = GKLM.
  Sind X, Y die Punkte, in welchen FH, GI den Durchmesser schneide, so sollen aus den verschiedenen Fällen, welche der Satz zulässt, für den Beweis hier folgende drei behandelt werden: 1) X und Y liegen zwischen E und D, 2) X liegt zwischen E und D, Y jenseit D, 3) X liegt zwischen E und D, Y jenseit E, aus welchen sich die andern Fälle, wenn X und Y jenseit D oder jenseit E liegen, leicht herleiten lassen.
  Beweis für Fall 1. Es ist nach III. 5
  1. ∆GYM - ∆OYD = ∆AOI,
  2. ∆FXL - ∆NXD = ∆ANH, woraus durch Subtraktion:
  • GKLM - FKYX + NOYX = NOIH, oder GKLM = FHIK.
  Für Fall 2. Es ist, wie oben, nach III. 5
  1. ∆GYM - ∆OYD = ∆AOI,
  2. ∆FXL-∆6NXD = ∆ANH, woraus durch Subtraktion:
  • GKLM - FKYX - ∆OYD + ∆NXD = NOIH oder GKML = FKON + NOIH = FHIK.
  Für Fall 3 kann zwar in ähnlicher Art als Fall (1) und (2) abgeleitet werden, kürzer aber folgendermassen:
  1. FNDL = ∆AHN,
  2. GODM = ∆AIO, nach III. 5
  • also GODM - FNDL = ∆AIO - ∆AHN
  • d. i. GYM - DYO - FXL + DXN oder GKLM - FXYK - NXYO = HNOI
  • OKFN = OKFN addirt, giebt
  • GKLM = FHIL. q. e. d.
• 
  Lehrsatz 13. Wenn in conjugirten Gegenschnitten zwei Tangenten an neben einander liegende Hyperbeln und die Durchmesser nach den Berührungspunkten gezogen werden, so ist ein Dreieck, dessen Ecken der Mittelpunkt, ein Berührungspunkt und der Durchschnittspunkt der in diesem gezogenen Tangente mit dem nach dem andern gezogenen Durchmesser sind, gleich dem ändern ähnlich gebildeten Dreieck.
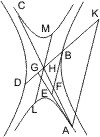  Seien A und B die Punkte der nebeneinander liegenden Hyperbeln, D der Durchschnitt der Tangente in A mit dem Durchmesser von B, E der der Tangente in B mit dem Durchmesser von A, so wird behauptet, dass
  • ∆CAD = ∆CBE.
  Man ziehe noch von A eine Parallele mit BE, welche CB in F schneidet. Es ist nun nach II. 20 und I. 38 CD : CB = CB : CF, aber CB : CF = CE : CA, also CD · CA = CB · CE und da die Winkel bei C in den beiden Dreiecken CAD und CBE entweder gleich oder supplementar sind, ist ∆CAD = ∆CBE.
• 
  Lehrsatz 14. Wird unter denselben Voraussetzungen als im vorigen Lehrsatz auf einer der nebeneinander liegenden Hyperbeln ein beliebiger Punkt angenommen und von ihm bis an den an diese Hyperbel gehenden Durchmesser Parallelen mit den Tangenten gezogen, so ist das hierdurch entstandene Dreieck gleich demjenigen, das die mit der Tangente an derselben Hyperbel gezogene Parallele mit den beiden Durchmessern bildet vermindert um das ähnliche Dreieck über dem an dieselbe gehenden Halbmesser.
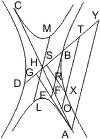  Seien wie vorher in den Punkten A und B zweier benachbarter Hyperbeln Tangenten und Durchmesser gezogen, die sich wechselseitig in D, E treffen, werden ferner von einem beliebigen Punkt F der Hyperbel B Parallelen FG, FH mit den Tangenten in A und B bis an den Durchmesser CB gezogen, von welchen FH den Durchmesser CA in I trifft, so wird behauptet.
  • ∆FGH = ∆CHI - ∆CBE.
  Man ziehe noch von A an den Durchmesser CB die Parallele AK mit BE. Ist nun r und t das latus rectum und transversum für den Durchmesser CB an der Hyperbel B, so ist:
  1. FH² : CH² - CB² = r : t,
  aber nach II. 20 und einer leichten Folgerung aus I. 38 auch:
  2. AK² : CK² + CB² = r : t, also
  3. FH² : AK² = CH² - CB² : CK²  + CB² oder
  4. ∆FGH : ∆ADK = ∆CHI - ∆CBE : ∆CKA + ∆CBE
  und da nach vorigem Satz ∆CBE = ∆CAD, ist ∆ADK = ∆CKA + ∆ CBE, also auch ∆FGH = ∆CHI - ∆CBE. q. e. d.
• 
  Lehrsatz 15. Wenn conjugirte Gegenschnitte gegeben sind und in zwei Punkten eines derselben Tangenten und Durchmesser, von einem Punkt einer der benachbarten Hyperbeln aber Parallelen mit den Tangenten bis an die Durchmesser gezogen werden, so ist das Dreieck, das diese Parallelen mit einem Durchmesser bilden, vermindert um das, welches die mit der Tangente im Endpunkt dieses Durchmessers gezogene Parallele mit beiden Durchmessern macht, gleich dem Dreieck, dessen Grundlinie eine Tangente (vom Berührungspunkte bis zum andem Durchmesser) und dessen Spitze der Mittelpunkt ist.
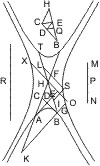  Seien in den Punkten A und B einer Hyperbel die Durchmesser AC, BC und die Tangenten AD, BE, die sich in K kreuzen, ferner von einem beliebigen Punkt F die Parallelen FG, FH mit den Tangenten AD, BE bis an den Durchmesser BC gezogen, FH aber treffe den andern Durchmesser AC in I, so wird behauptet:
  • ∆FGH - ∆CHI = ∆BEC.
  Man ziehe von A eine Parallele AX mit BE bis an den Durchmesser CB.
  Nun ist
  1. ∆FGH : ∆ADX = FH² : AX² = CB²  + CH² : CX²  - CB² (siehe vorigen Beweis)
     = ∆CBE + ∆CHI : ∆CAX - ∆CBE
  2. und da nach I. 43 ∆ADX = ∆CXA - ∆CBE, so ist auch ∆FGH = ∆CBE + ∆CHI. q. e. d.
  Wenn unter denselben Voraussetzungen von zwei beliebigen Punkten der benachbarten Hyperbel Parallelen mit den Tangenten gezogen werden, so sind zwei Vierecke, aus je drei dieser Parallelen und einem Durchmesser so gebildet, dass jedes an einen der angenommenen Punkte anstösst, einander gleich.
  Seien ausser den oben gezogenen Linien noch von einem zweiten Punkt K der Hyperbel F die Parallelen KL, KM an die Durchmesser BC, AC gezogen, deren letztere den Durchmesser BC in N schneidet, und sei O der Kreuzungspunkt von FH mit KL, so wird behauptet: FGLO = KMIO.
  Es ist nach dem, was oben bewiesen:
  1. ∆FGH - ∆CHI = FGCI = ∆BCE,
  2. ∆KLN - ∆CNM = KLCM = ∆BCE,
  also FGCI = KLCM, und wenn man LCIO auf beiden Seiten abzieht, bleibt FGLO = KMIO. q. e. d.
• 
  Lehrsatz 16. Wenn zwei Tangenten eines Kegelschnitts sich schneiden und von einem beliebigen Punkt des letzteren mit einer der Tangenten eine Parallele gezogen wird, welche sowohl den Kegelschnitt zum zweiten Male als die andere Tangente trifft, so verhält sich das Quadrat des hierdurch auf der Tangente vom Berührungspunkt an abgeschnittenen Stücks zum Rechteck der beiden Abschnitte, auf der Parallelen, beide von der Tangente an gerechnet, wie das Quadrat der einen Tangente zum Quadrat der andern.
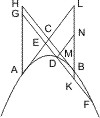  Seien A und B zwei Punkte eines Kegelschnitts, deren Tangenten sich in D schneiden, und von einem beliebigen Punkt E des Umfangs eine Parallele mit BD gezogen, die den Schnitt zum zweiten Mal in F und die Tangente AD in G schneidet, so wird behauptet:
  • AG² : GE · GF = AD² : BD².
  Seien H,M die Durchschnittspunkte von AD und GF mit dem Durchmesser BC, I und K die Durchschnitte von DB und GF mit dem Durchmesser AC und werde von E eine Parallele mit AD gezogen, die BC in L trifft. Nun ist:
  • AG² : AD² = ∆AGK : ∆ADI
  • = ∆ADI + GMBD - MBIK : ∆ADI
  • = ∆BDH + GMBD - ∆ELM : ∆BDH nach III. 1 und I,43
  • = ∆HGM -  ∆ : ∆BDH
  • = GM² - ME² : BD²
  • = GE · GF :BD² q.e.d.
  Der Beweis gilt an folgenden Fig., und mit einziger Aenderung der Zeichen für alle übrigen Fälle:
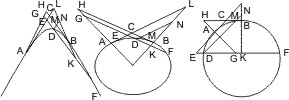
  Wenn bei einer Ellipse oder einem Kreise die nach den Berührungspunkten gezogenen Durchmesser den Tangenten parallel sind, so findet das oben Behauptete gleichfalls Statt, und kann folgendermassen bewiesen werden.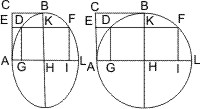 Es ist in Fig. rechts, in welcher ausser den im Satz erwähnten Linien nur noch die Ordinate EN an den Durchmesser AC gezogen und X der zweite Durchschnitt von AC mit dem Kegelschnitt ist,
  1. EN² : AN · NX = BC² : AC², also
  2. AG² : GM² - ME² = AD : BD² oder endlich
  3. AG² : GE · GF = AD : BD. q.e.d.
• 
  Lehrsatz 17. Wenn an einem Kegelschnitt, zwei sich schneidende Tangenten gezogen sind und von zwei andern beliebigen Punkten desselben je eine Parallele mit einer Tangente gezogen wird, so dass diese Parallelen sich selbst und den Kegelschnitt noch in einem zweiten Punkt treffen, so verhält sich das Rechteck aus den auf einer dieser Linien gebildeten Abschnitten, vom Kreuzungspunkt der Parallelen bis zum Kegelschnitt gerechnet, zu dem andern ähnlich gebildeten Rechteck wie das Quadrat der der ersten Linie parallelen Tangente zum Quadrat der andern.
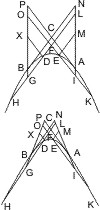  Seien in den Punkten A und B eines Kegelschnitts Tangenten gezogen, die sich in D treffen, und von zwei andern Punkten desselben, E und F, von E eine Parallele mit BD, von F mit AD, welche Parallelen den Kegelschnitt beziehlieh in G und H, sich selbst in X schneiden, so wird behauptet:
  • EX · XG : FX · XH = BD² : AD².
  Construction. Construction. Man ziehe die Durchmesser AC, BC, welche den Tangenten BD, AD in den Punkten S und Q begegnen, ferner von E eine Parallele mit AD, welche BC in O, und von F eine Parallele mit BD, welche AC in R trifft, nenne die Punkte, in welchen EG die Durchmesser AC, BC schneidet, K und L, und die, in welchen FH dieselben trifft, I, P.
  Beweis. Nun ist:
  1. EL² : XL² = ∆ELO : ∆XLP, also
  2. EL² - XL² : ∆ELO - ∆XLP = EL² : ∆ELO = BD² : ∆BDQ,
  ferner auf gleiche Weise:
  3. FI² : XI² ∆FIR : ∆XIK, also
  4. FI² -XI² ∆FIR - ∆XIK = FI² : ∆FIR = AD² : ∆ADS.
  Da nun ∆ELO - ∆XLP = EXPO und ∆FIR - ∆XIK = FXKR, und nach III. 3 EXPO = FXKR und nach III. 1 ∆BDQ = ∆ADS, und da EL² - XL² = EX · XG und FI² - XI² = FX · XH, folgt aus Vergleichung von (2) und (4):
  • EX · XG : FX · XH = BD² : AD². q. e. d.
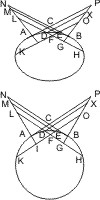  Wenn bei einer Ellipse oder einem Kreise die beiden Tangenten so gezogen sind, dass die Durchmesser nach den Berührungspunkten ihnen parallel sind, so findet das oben Behauptete gleichfalls Statt und kann folgendermassen bewiesen werden.
  Es ist, wenn die Linien, wie oben gezogen und benannt sind,
  1. EL² : BC² - IX² = AC² : BC²,
  2. FI² : CA² - XL² = BC² : AC², also
  3. EL² BC² - IX² = CA² - XL² : FI² = AC² : BC², also auch
  4. CA² + EL² - XL² : CB² + FI² - XI² = AC² : BC² oder
  5. CA² + EX · XG : CB² + FX · XH = AC² : BC²,
  woraus man leicht erhält: EX · XG : FX · XH = AC² : BC² = BD² : AD².
  Anm. Hieraus ergiebt sich leicht, dass, wenn von einem Punkt zwei Linien durch einen Kegelschnitt gezogen werden, das Verhältniss des Rechtecks aus den Abschnitten der einen zu dem aus den Abschnitten der andern gleich demselben Verhältniss für zwei von einem beliebigen andern Punkte parallel den ersten gezogene Linien ist.
• 
  Lehrsatz 18. Wenn an zwei Gegenschnitte zwei sich schneidende Tangenten und von einem beliebigen Punkt eines der beiden Gegenschnitte eine Parallele mit einer Tangente gezogen werden, bis letztere sowohl die andere Tangente als die Gegenschnitte zum zweiten Male schneidet, so ist das Quadrat des hierdurch auf der Tangente abgeschnittenen Stücks zum Rechteck aus den Abschnitten auf der Parallelen (beide von der Tangente an gerechnet) wie das Quadrat der einen Tangente zu dem der andern.
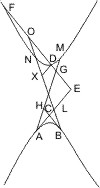  Seien in den Punkten A und B zweier Gegenschnitte Tangenten gezogen, die sich in D kreuzen, und von einem andern beliebigen Punkte E eine Parallele mit BD, welche die Gegenschnitte zum zweiten Mal in F und die Tangente AD in G trifft, so wird behauptet (wie in § 16):
  • AG² : GE · GF = AD² : BD².
  Man ziehe noch in A und B die Durchmesser, deren ersterer BD in I, GE in K und deren letzterer AD in H, GE in M schneidet, endlich von E an den Durchmesser BM die Linie EL parallel AD. Nun ist:
  • MG² : ME² = ∆MGH : ∆MES, also
  • MG² - ME² : LEGH = MG³ : ∆MGH = BD² : ∆BDH,
  und da nach III. 6 LEGH = ∆AKG und nach III. 1 ∆BDH = ∆ADI, so ist MG² - ME² : ∆AKG = BD² : ∆ADI, oder wenn die inneren Glieder vertauscht werden und statt ∆AKG : ∆ADI gesetzt wird AG² : AD², sowie statt MG² - ME² GE · GF:
  • GE · GF : BD² = AG² : AD² oder
  • AG² : GE · GF = AD² : AD². q.e.d.
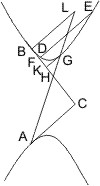  Ein anderer Beweis für den Fall, in welchem die Punkte A und B nicht auf derselben Hyperbel liegen, ist folgender. Sei die Bezeichnung vor der Construction des Beweises wie oben und werden von den Punkten β, wo der von B gezogene Durchmesser den Gegenschnitt trifft, und von A die Parallelen βδ und AO an die Linien AD und Bβ gezogen.
  Nun ist:
  • Aδ : δH = Oβ : βH = OB : HB = AD : DH, also
  • Aδ : AD = δH : DH und da
  • δH : DH = βδ : DB, auch
  • Aδ : δβ = AD : BD;
  • da aber nach § 16
  • AG² GE · GF = Aδ² : δβ, ist nun auch
  • AG² GE · GF = AD² : BD². q.e.d.
• 
  Lehrsatz 19. Wenn an zwei Gegenschnitte zwei sich schneidende Tangenten und mit diesen zwei Parallelen gezogen werden, deren jede die Schnitte in zwei Punkten trifft, so verhält sich das Rechteck aus den Abschnitten auf der einen Parallelen, von dem Scheidungspunkt der Parallelen bis zu den beiden Punkten auf dem Kegelschnitt gerechnet, zu dem ähnlich gebildeten Rechteck auf der andern Parallelen wie das Quadrat der einen Tangente zu dem Quadrat der andern.
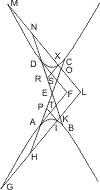  Seien in den Punkten A und B die sich in D kreuzen den Tangenten an zwei Gegenschnitten und von zwei andern Punkten E und F, von ersterem eine Parallele mit BD, von letzterem mit AD gezogen, welche Parallelen die Gegenschnitte noch in den Punkten G und H und sich gegenseitig in X treffen, so wird behauptet, wie in § 17:
  • XE · XG : XF · XH = BD² : AD²
  Man ziehe noch von A und B die Durchmesser, deren ersterer XF in I, BD in S, XE in K, deren letzterer XE in L, AD in Q, XI in P trifft, und von E an BQ die Linie EO parallel AD, sowie von F an AK die Linie FR parallel BD.
  Nun ist:
  1. IX² : ∆IXK = IF² : ∆IFR = AD² : ∆ADS,
  2. LX² : ∆LXP = LE² : ∆LEO = BD² : ∆BDQ, also
  3. LX² - IF² : XKRF = AD² : ∆ADS und
  4. LX² - LE² : XPOE = BD² : ∆BDQ,
  weil aber nach III.7 XPOE = XKRF und nach III.5 ∆BDQ = ∆ADS ist
  5. XF · XH : XE · XG = AD² : BD². q.e.d.
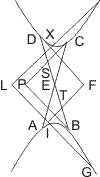  Fällt der Punkt X nicht ausserhalb, sondern innerhalb des Winkelraums BDA, so ziehe man die Durchmesser Aα, Bβ, ziehe in α und β die Tangenten, welche sich in δ schneiden, nenne S und ς die Punkte, in welchen BD, βδ die Linie Aα, und T und τ diejenigen, in welchen AD und αδ die Linie Bβ durchschneiden, so ist ∆BSC congruent ∆αςC, ∆ATC congruent ∆ατC, ∆ASD congruent ࢞αζδ, ∆BTD congruent ∆βτδ, weshalb AD = αδ und BD = βδ, und da der Punkt X ausserhalb des Winkelraums -δβ liegen muss, wenn die von ihm mit den Tangenten gezogenen Parallelen die Gegenschnitte treffen sollen, ist hierdurch dieser Fall auf den vorigen zurückgeführt.
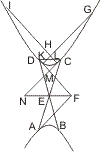
  Fällt endlich der Punkt X, innerhalb einer Hyperbel, so sei wieder Aα der von A gezogene Durchmesser, αδ die Tangente in α, dann ist im zweiten Beweis von § 18. gezeigt, dass
  • αδ : Bδ = AD : BD und in § 17
  • XE · XG : XF : XH = Bδ² : αδ², also auch
  • = BD² : AD².
  Anm. Hieraus ergiebt sich leicht die Folgerung: Zieht man von einem beliebigen Punkt zwei Gerade, welche zwei Gegenschnitte in je zwei Punkten schneiden, so ist das Verhältniss des Rechtecks aus den Abschnitten der einen zu dem aus den Abschnitten der andern gleich demselben Verhältniss für zwei von einem beliebigen andern Punkt mit den ersten Geraden gezogene Parallelen.
• 
  Lehrsatz 20. Wenn an zwei Gegenschnitte zwei sich schneidende Tangenten und durch ihren Schneidungspunkt sowohl als durch irgend einen andern Punkt der Gegenschnitte Parallelen mit der Berührungssehne gezogen werden, so verhält sich das Quadrat des durch die letzte Parallele auf einer Tangente abgeschnittenen Stücks zu dem Rechteck aus den Abschnitten auf der Parallele selbst von der Tangente bis zu den Gegenschnitten gerechnet, wie das Quadrat dieser Tangente vom Berührungspunkt bis zum Kreuzungspunkt der Tangenten, zu dem Quadrat der halben durch diesen Kreuzungspunkt gezogenen Parallelen.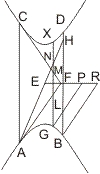
  Seien in den Punkten A und B zweier Gegenschnitte Tangenten gezogen, die sich in D kreuzen, und durch D sowohl als durch einen beliebigen Punkt F eines Gegenschnitts die Parallelen DE, FGH mit der Berührungssehne AB gezogen, so wird behauptet:
  • AG² : FG · GH = AD² : ED²
  Man ziehe den Durchmesser AC, welcher FG in K, ED in L, und DC, welcher FG in I schneidet, ferner durch F und E an CD die Linien FM, EN parallel mit AD. Nun ist:
  • AG² : AD² = ∆AGK : ∆ADL,
  aber nach III.5 ∆ = ∆IFM - ∆IGD und ∆ADL = ∆EDN und ∆IFM - ∆IGD : ∆EDN = IF² - IG² : ED² = FG · GH : ED², ist also AG² : AD² = FG · GH : ED². q.e.d.
• 
  Lehrsatz 21. Werden an zwei Gegenschnitte zwei sich schneidende Tangenten und die Berührungssehne, von einem beliebigen Punkt eines Schnittes aber eine Parallele mit einer Tangente und von einem andern eine Parallele mit der Berührungssehne gezogen, welche Parallelen sowohl sich selbst als die Gegenschnitte schneiden, so verhält sich das Rechteck aus den Abschnitten der ersten Parallelen zu dem aus den Abschnitten der zweiten (vom Kreuzungspunkt der Parallelen bis an die Gegenschnitte gerechnet), wie das Quadrat der Tangente bis zum Berührungspunkt zum Quadrat der halben durch den Kreuzungspunkt der Tangenten bis an die Gegenschnitte gezogenen Parallelen mit der Berührungssehne.
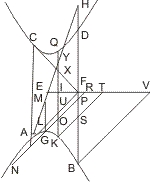  Seien in den Punkten A und B Tangenten gezogen, die sich in D kreuzen, von dem Punkte F eines der Schnitte eine Parallele mit AD, welche dem Schnitt zum zweiten Mal in H, den Durchmessern CA, CD in K und P begegnet, und von einem andern Punkt G des Schnitts eine Parallele mit AB, welche dem zweiten Schnitt in I, der von F gezogenen Parallelen in X und den Durchmessern CA, CD in M, O begegnet, werde ferner durch D eine Parallele mit AB gezogen, die den einen Schnitt in E trifft, so wird behauptet:
  • XF · XH : XG · XI = AD² : ED²
  Man ziehe noch durch F eine Parallele mit AB, die AC in L, durch G und E Parallelen mit AD, die CD in Q und R treffen, und nenne N den Durchschnitt von ED mit AC. Nun ist:
  1. XK² : KF² = ∆XKM : ∆FKL,
  2. OG² OX² = ࢞OGQ : ∆OXP, also
  3. XK² - KF² : FLMX = XK² : ∆XKM = AD² : ∆ADN
  4. OG² - OX² : GXPQ = OG² : ∆OGQ = ED² : ∆EDR
  und da nach III.12 FLMX = GXPQ und nach III.5 ∆ = ∆EDR, erhält man
  5. XK² - KF² : OG² - OX² = AD² : ED² oder XF · XH : XG · XI = AD² : ED². q.e.d.
• 
  Lehrsatz 22. Wenn an zwei Gegenschnitte ein Querdurchmesser, und eine beliebige Parallele damit, so wie eine andere mit der zugehörigen Ordinatenrichtung gezogen werden, welche Parallelen sowohl sich selbst als die Gegenschnitte treffen, so verhält sich das Rechteck ans den Abschnitten auf der ersten zu dem Rechteck. auf den Abschnitten der letzteren wie das latus transversum zum latus rectum.
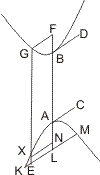  Sei AB ein Querdurchmesser zweier Gegenschnitte und werde damit eine Parallele gezogen, die die Schnitte in F und G, so wie eine andere mit der zugehörigen Ordinatenrichtung, die die erste Parallele in H, die Gegenschnitte in D,E trifft, so wird behauptet:
  • HF · HG : HD · HE = t : r,
  Sei I der Durchschnitt von DE mit AB und werde noch von F die Ordinate FK gezogen, so ist
  1. DI² : IC² - AC² = FK² : KC² = r : t, also
  2. DI²- FK² : IC² - KC² = r : t, aber
  3. DI² - FK² = HD · HE und IC² - KC² = HF · HG, also
  4. HD · HE : HF · HG = r : t. q.e.d.
     
• 
  Lehrsatz 23. Wenn conjugirte Schnitte und an zwei gegenüberliegenden derselben zwei Tangenten gegeben sind, welche sich innerhalb eines der benachbarten Schnitte treffen, und wenn zwei Parallelen mit diesen Tangenten gezogen werden, solche sowohl sich selbst als diese benachbarten Schnitte treffen, so verhalten sich die Rechtecke aus den Abschnitten auf diesen Parallelen wie die Quadrate der Tangenten.
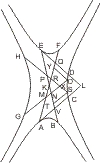  Seien in den Punkten A und B zweier Gegenschnitte Tangenten gezogen, die sich innerhalb eines der benachbarten conjugirten Schnitte in D kreuzen und mit diesen Tangenten zwei Parallelen, die sich gegenseitig in X und die den Hyperbeln A und B conjugirten Schnitte in E, F, G, H treffen, so wird behauptet:
  • XE · XF : XG · XH = AD² : BD².
  Man ziehe die Durchmesser AC, BC, welche der Geraden EF in L, K, der Geraden GH in M, I begegnen, ziehe von E eine Parallele mit BD, die AC in P und von G eine Parallele mit AD, die BC in N trifft; ist nun noch R der Durchschnitt von AD und BC, Q der von BD und AC, so ist
  1. EL² : ∆ELP = XL² : ∆XLM = AD² : ∆ADQ,
  2. GI² : ∆GIN = IX² : ∆IXK = BD² : ∆BDR, also auch
  3. EL² - XL² : XEPM = AD² : ∆ADQ und
  4. GI² - XI² : GXKN = BD² : ∆BDR,
  und das nach III.5 XEPM = GXKN und nach III.4 ∆ADQ = ∆BDR, so folgt:
  5. EL² - XL² : GI² - XI² = AD² : BD² oder
  6. XE · XF : XG · XH= AD² : DB². q.e.d.
• 
  Lehrsatz 24. Wenn in conjugirten Gegenschnitten zwei conjugirte Durchmesser und zwei Parallelen mit diesen gezogen werden, die sich in dem Raum zwischen den Schnitten begegnen, so ist das Rechteck aus den Abschnitten der ersten Parallelen vermehrt um ein anderes, zu welchem sich das Rechteck aus den Abschnitten der andern Parallelen ebenso verhält wie das Quadrat des zweiten Durchmessers zu dem des ersten, gleich dem halben Quadrat dieses ersten Durchmessers.
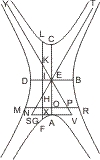  Seien AB, DE conjugirte Durchmesser an zwei Paaren conjugirter Gegenschnitte und eine Parallele mit AB, die die Gegenschnitte A und B in G und H trifft, sowie eine andere mit DE, die die Gegenschnitte D und E in I und K trifft, gezogen, ist nun F der Durchschnittspunkt dieser Parallelen, so wird behauptet:
  • GF · FH + CA² ⁄ CD² · KF · FI = 2 · CA².
  Sei L der Durchschnitt von AB und IK, M der von DE und G H, so ist
  1. GM² - CA² : LF² = CA² : CD²,
  2. MF² : LI² _ CD² = CA² : CD², also
  3. GM² -CA² : LF² = MF² : LI² - CD² = CA² : CD² und
  4. GM² - MF² - CA² : LF² - LI² + CD² = CA² : CD², woraus componendo leicht folgt:
  5. HF · FG : 2 · CD² - KF · FI = CA² : CD², also
  6. HF · FG = 2 · CA² - CA² ⁄ CD² · KF · FI. q.e.d.
  Oder von Zeile 2 an etwas kürzer:
  3. GM² : LF² + CD² = MF² + 2 · CA² : LI² + CD² = CA² : CD² und
  4. MF² - GM² + 2 · CA² : LI² - LF² = CA² : CD² oder
  5. 2 · CA² GF · FH = IF · FK CA² ⁄CD². q.e.d.
  Anm. Dieser Beweis gilt ohne Aendernng auch für die Fälle, in welchen der Schneidungspunkt der Parallelen innerhalb der einen oder der andern Hyperbel liegt, wobei nur zu merken. ist, dass jedes der Rechtecke GF · FH oder KF · FI sein Zeichen wechselt, sobald der Punkt F die Hyperbel überschreitet, durch deren Durchschnittspunkte es gebildet ist. Diese Fälle behandelt Apollonius besonders im 25. und 26. Lehrsatz, die ich wegen des geringen Unterschiedes mit dem 24. nicht besonders beweise. Liegt der Schneidungspunkt in einer Hyperbel selbst, so reducirt sich die Behauptung auf die des Lehrsatzes 22. im 2. Buche. Um jedoch auch den Gang des Apollonischen Beweises anzugeben, folgt derselbe hier für den Fall, dass der Schneidungspunkt der Parallelen innerhalb des Asymptotenwinkels liegt.
  Seien in der vorigen Figur noch die Asymptoten gezogen, welche die in A gezogene Tangente in N und O, die Parallele GH in den Punkten P und Q und die Parallele IK in R und S treffen. Nun ist, weil CD = AN und ∆CAN ~ ∆PFR, so wie ∆CAO ~ ∆QFS
  1. CA : AN = PF : FR und
  2. CA : AO = QF : FS, also
  3. CA² : CD² = FP · FQ : FR · FS
  Es ist aber:
  • FP · FQ = MF² - MP² = MG²- MP² - MG² + MF²
  • = GP · GQ - FG · FH
  • und nach II.10 = CA² - FG · FH.
  Ferner auf ähnliche Art:
  • FR · FS = LR² - LF² = LI² - LF² -LI² + LR²
  • =FI · FK - IR · IS
  • und nach II.10 =FI · FK - CD².
  Setzt man diese Werthe oben in 3. ein, so erhält man
  4. CA² : CD² = CA² - FG · FH : FI · FK - CD² oder
     2 · CA² - FG · FH : FI · FK = CA² : CD². q.e.d.
• 
  Lehrsatz 27. Wenn in einer Ellipse oder einem Kreis conjugirte Durchmesser und mit diesen je eine Parallele gezogen werden, welche sich selbst und den Kegelschnitt schneiden, so ist die Summe der Quadrate der Stücke auf der Parallelen mit dem ersten Durchmesser, vom gegenseitigen Durchschnitt bis zum Kegelschnitt gerechnet, vermehrt um die Summe zweier Rechtecke über den Stücken der andern Parallelen, welche ähnlich und ähnlich gelegen sind mit dem Rechteck aus dem zweiten Durchmesser und seinem zugehörigen latus rectum, gleich dem Quadrat des ersten Durchmessers.
  
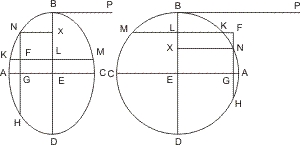  Seien AB, DE conjugirte Durchmesser einer Ellipse, GH, IK Parallelen damit, die sich in F kreuzen, r das zum zweiten Durchmesser DE gehörige latus rectum, so wird behauptet:
  • FG² + FH² + FI² · r ⁄ DE + FK² · r ⁄ DE = AB².
  Beweis. Sei noch L der Durchschnitt von IK und AB, M der von GH und DE, so ist:
  1. FG² + FH² = (MG - MF)² + (MG + MF)² = 2 · MG² + 2 · MF² = 2 · DM · ME · r ⁄ DE + 2 · CL².
     Es ist aber
  2. DM · ME · r ⁄ DE = DC² · r ⁄ DE - MC² · r ⁄ DE = AC² - FL² · r ⁄ DE,
  weil r ⁄ DE = AC² ⁄ DC² ist, ferner, weil IL² = CA² · DE ⁄ r - CL² · DE ⁄ r, erhält man leicht
  3. CL² = CA² - IL · r ⁄ DE.
  Setzt man (2) und (3) in (1) ein, so hat man
  4. FG² + FH² = 2 · CA² - r ⁄ DE + 2 · CA² - 2 · IL² · r ⁄ DE =
     = 4 · CA² - 2 · FL² · r ⁄ DE,
  und da endlich
  • 2 · IL² + 2 · FL² = 2 · (½ · (FK + FI))sup>2 + 2 · (½ · (FK - FI))² = FK² + FI²
  ist, so erhält man
  5. FG² + FH² = AB² - FK² · r ⁄ VE - FI² · r ⁄ VE. q.e.d.
• 
  Lehrsatz 28. Wenn in conjugirten Gegenschnitten conjugirte Durchmesser und mit diesen je eine Parallele gezogen werden, so verhält sich die Summe der Quadrate der Abschnitte auf einer dieser Parallelen, von ihrem gegenseitigen Kreuzungspunkt bis an das eine Paar Gegenschnitte gerechnet, zu der Summe der Quadrate der Stücke auf der andern bis zu den andern Gegenschnitten gerechnet, wie das Quadrat des zur ersten Parallele gehörigen Durchmessers zu dem Quadrat des zur zweiten gehörigen.
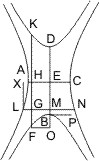  Seien AB, DE conjugirte Durchmesser zweier conjugirter Gegenschnitte, GH, IK Parallelen damit, die sich in F kreuzen, so wird behauptet:
  • FI² + FK² : FG² + FH² = DE² : AB².
  Man ziehe noch von G die Ordinate GN an den Durchmesser AB, und von I die Ordinate IO an DE, und nenne L den Schneidungspunkt von IK und AB, M den von GH und DE, so ist
  1. GN² : CN² - CA² = CD² : CA²,
  2. CO² - CD² : IO² = CD² : CA², also
  3. GN² + CO² - CD² : CN² - CA² + IO² = CD² : CA², oder auch
  4. GN² + CO² : CN² + IO² = CD² : CA², aber
  • GN² + CO² = FL² + LI² = ½ · (FI² + FK²) nach dem, was im vorigen Satz bewiesen; und ebenso
  • CN² + IO² = MG² + MF² = ½ · (FG² + FH²), welches in (4) eingesetzte, ergiebt:
  • FI² + FK² : FG² + FH² = CD² : CA². q.e.d.
• 
  Lehrsatz 29. Unter denselben Voraussetzungen als im vorigen Lehrsatz verhält sich die Summe der Quadrate der Stücke auf einer Parallelen, vom Kreuzungspunkt derselben bis zu den Asymptoten gerechnet, vermehrt um das halbe Quadrat des parallelen Durchmessers zu der Summe der Quadrate der Stücke auf der andern Parallelen, von ihrem Kreuzungspunkt bis zu den Gegenschnitten gerechnet, wie das Quadrat des einen Durchmessers zu dem des andern.
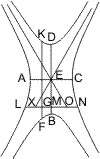  Seien P und Q die Durchschnittspunkte der Parallelen IK mit den Asymptoten, so wird behauptet, dass
  • FP² + FQ² + ½ · DE² : FG² + FH² = DE² : AB² ist.
  Beweis. Vergleicht man diese Behauptung mit der des vorigen Lehrsatzes, so zeigt sich, dass man beweisen muss:
  • FI² + FK² = FP² + FQ² + ½ · DE², oder
  • FI² + FK² - FP² - FQ² = ½ · DE².
  Es sei nun zuerst F zwischen Q und P gelegen, so hat man
  • FI² - FP² + FK² - FQ² = IP · (FI + FP) + KQ · (FK + FQ) oder da nach II.8 KQ = IP:
  • FI² - FP² + FK² - FQ² = IP · (FI + FP + FK + FQ) =
  • = IP · (IK + PQ) =
  • = IP · (2 · PQ + 2 · IP) =
  • = 2 · IP · IQ =
  • 2 · CD² = (nach II.16)
  • ½ · DE².
  Ein ähnlicher Beweis findet Statt, wenn F zwischen P und I liegt.
• 
  Lehrsatz 30. Wenn von einem Punkt innerhalb des Asymptotenwinkels einer Hyperbel an dieselbe zwei Tangenten und eine Parallele mit einer Asymptote gezogen werden, so wird das Stück der letzteren zwischen dem Ausgangspunkt und der Berührungssehne der Tangenten von der Hyperbel halbirt.
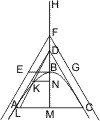  Sei D ein Punkt innerhalb des Asymptotenwinkels einer Hyperbel, DA, DB die Tangenten an dieser, DF eine Parallele mit der einen Asymptote, welche die Hyperbel in E, die Berührungssehne in F trifft, so wird behauptet:
  • DE = EF.
  Man ziehe vom Mittelpunkt C durch D einen Durchmesser, der die Hyperbel in I, AB in G trifft, von E an diesen Durchmesser die Ordinate EH und in J die Tangente, die eine Asymptote in K trifft. Nun ist:
  1. EH² : HD² = KI² : CI²
  wegen Aehnlichkeit der Dreiecke EHD und KIC,
  2. EH² : HC² - CI² = KI² : CI²,
  weil KI gleich dem halben zweiten Durchmesser der Hyperbel nach II.3. Hieraus folgt aber:
  • HD² = HC² - CI², und weil
  • CI² = CD · CG nach I.37.
  • CD · CG = HC² - HD² = CD · (HC + HD), woraus
  • CG = HC + HD, und wenn man auf beiden Seiten CD abzieht:
  • DG = 2 · HD, weshalb
  • DH = HG und DE = EF. q.e.d.
• 
  Lehrsatz 31. Wenn von einem Punkt ausserhalb des Asymptotenwinkels an zwei Gegenschnitte je eine Tangente und mit einer Asymptote eine Parallele gezogen werden, so wird das Stück dieser letzteren vom Ausgangspunkt bis zur verlängerten Berührungssehne von der einen Hyperbel halbirt.
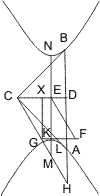  Seien von einem Punkt D ausserhalb des Asymptotenwinkels zweier Gegenschnitte an diese die Tangenten DA, DB und mit der einen Asymptote eine Parallele gezogen, welche die Berührungssehne in F und den Gegenschnitt A in E trifft, so wird behauptet:
  • DE = EF.
  Beweis. Man ziehe noch den Durchmesser DC, welcher AB in G trifft, ferner von E an CD die Ordinate EH, so wie von C den mit AB parallelen Halbmesser CI und in I die Tangente IK bis zu der Asymptote, mit welcher die Parallele DF gezogen ist. Nun ist:
  1. EH² : HD² = CI² : IK²
  wegen Aehnlichkeit der Dreiecke EHD, CIK,
  2. EH² : CH² + IK² = CI² : IK²
  nach I.38, II.3 und einer leichten Folgerung daraus. Also
  • HD² = CH² + IK², und da nach I.38 auch
  • IK² = CG · CF, CG · CD = HD² - CH² = CD · (HD - CH), also
  • CG = HD - CH, oder wenn man CH auf beiden Seiten addiert,
  • GH = HD, also auch FE = ED. q.e.d.
• 
  Lehrsatz 32. Wenn von einem Punkt innerhalb des Asymptotenwinkels einer Hyperbel Tangenten an diese und eine Parallele mit der so entstandenen Berührungssehne, von der Mitte dieser letzteren aber eine Parallele mit einer Asymptote gezogen werden, so wird das Stück dieser Parallelen zwischen ihrem Ausgangspunkt und der vom Ausgangspunkt der Tangenten gezogenen Parallelen von der Hyperbel halbirt.
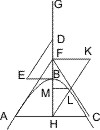  Seien von einem Punkt D innerhalb des Asymptotenwinkels einer Hyperbel an diese zwei Tangenten DA, DB, die Berührungssehne AB und von ihrer Mitte G eine Parallele mit einer Asymptote gezogen, welche die von D mit AB gezogene Parallele in F, die Hyperbel in E trifft, so wird behauptet:
  • GE = EF
  Beweis. Man ziehe den Durchmesser CDG, von E daran die Ordinate EH, ferner im Scheitel I die Tangente, bis sie die mit GF parallele Asymptote in K trifft. Nun ist:
  1. EH² : HG² = IK² : CI²
  wegen Aehnlichkeit der Dreiecke EHG und CIK,
  2. EH² : CH²- CI² = IK² : CI², woraus
  • HG² = CH² - CI², und da CI² = CD · CG,
  • CD · CG = CH² - HG² = CG · (CH - HG) oder
  • CD = CH - HG, d. h. HG = CH _ CD = DH,
  • mithin auch GE = EF. q.e.d.
• 
  Lehrsatz 33. Wenn von einem Punkt ausserhalb des Asymptotenwinkels zweier Gegenschnitte an diese je eine Tangente, und mit der so entstandenen Berührungssehne eine Parallele, von der Mitte der Berührungssehne aber eine Parallele mit einer Asymptote gezogen werden, so wird das Stück dieser Parallele von der Berührungssehne bis zu der vom Ausgangspunkt der Tangenten damit gezogenen Parallelen durch die Hyperbel halbirt.
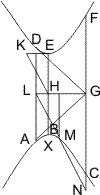  Seien von einem Punkt ausserhalb des Asymptotenwinkels zweier Gegenschnitte an diese die Tangenten DA, DB, und von der Mitte G der Berührungssehne eine Parallele mit einer Asymptote gezogen, welche die Hyperbel in B, eine von D mit AB gezogene Parallele aber in F trifft, so wird behauptet:
  • GE = EF
  Man ziehe noch den Durchmesser GCD, von E daran die Ordinate EH, ferner von C den mit BA parallelen Halbmesser CI und im Scheitel I die Tangente, bis sie die mit GF parallele Asymptote in K trifft, so ist:
  1. EH² : HG² = CI² : IK²
  wegen Aehnlichkeit der Dreiecke EHG, CIK,
  2. EH² : HC² + IK² = CI² : IK²
  aus I.38, II.3 und einer leichten Folgerung daraus. Also
  • HG² = HC² + IK², aber
  • IK² = CG · CH nach I.38, mithin
  • CG · CD = HG² - HC² = CG · (HG + HC), oder
  • CD = HG + HC, also HD = HG, weshalb auch GE = EF. q.e.d.
• 
  Lehrsatz 34. Wenn von einem Punkt in einer Asymptote einer Hyperbel an diese eine Tangente und eine Parallele mit der andern Asymptote gezogen werden, so wird das Stück dieser Parallelen von ihrem Ausgangspunkt bis zu einer durch den Berührungspunkt der Tangente mit der ersten Asymptote gezogenen Parallelen durch die Hyperbel halbirt.
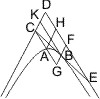  Seien von einem Punkt D in einer Asymptote einer Hyperbel an diese eine Tangente DA und eine Parallele mit der andern Asymptote gezogen, welche die Hyperbel in E und eine vom Berührungspunkt A mit der Asymptote CD gezogene Parallele in F trifft, so wird behauptet:
  • DE = EF.
  Sei B der Punkt, in dem DA die zweite Asymptote trifft, und noch von A an CD eine Parallele H mit BC gezogen, so ist nach II.12:
  CH · HA = CD · DE, da aber nach II.3 DA = AB, also auch DH = HC oder CH = ½ · DC, muss auch HA = 2 · DE oder, was dasselbe ist, DE = EF sein. q.e.d.
  Anderer Beweis. Man ziehe EA, welche verlängert die Asymptote CB in K, CD in I trifft, so ist, weil DA = AB, auch EA = AK, aber AK = IE (II.8), folglich auch IE = EA und daher DE = EF. q.e.d.
• 
  Lehrsatz 35. Wenn von einem Punkt in einer Asymptote einer Hyperbel eine Tangente an diese und eine beliebige andere Linie, die die Hyperbel in zwei Punkten trifft, durch den Berührungspunkt der Hyperbel aber eine Parallele mit dieser Asymptote gezogen werden, so verhält sich auf der beliebig gezogenen Geraden das Ganze zum äusseren Stück wie die beiden Stücke innerhalb der Hyperbel.
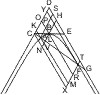  Seien von einem Punkt D in einer Asymptote einer Hyperbel eine Tangente DA und eine beliebige Linie gezogen, die die Hyperbel in E, F trifft, durch den Berührungspunkt aber eine Parallele mit CD, die EF in G schneidet, so wird behauptet:
  • DE : DF = GR : GF.
  Beweis. Man ziehe von E, A, F Parallelen mit den Asymptoten CD, CB, welche diese beziehlich in den Punkten I und K, L und M, N und O treffen, nenne H den Punkt, in welchem DF die zweite Asymptote trifft. Nun ist nach II.12:
  1. CI · IE = CL · LA = CN · NF, mithin
  2. CI : CL = LA : IE,
  3. CL : CN = NF : LA, also
  4. IL : CL = IE - LA : IE und
  5. LN : CL = LA - NF : NF,
  da aber DA = AB nach II.3 ist auch DM = MC, und da DE = FH nach II.8, ist auch DK = CO, mithin KM = MO oder IE - LA = LA - NF, folglich ergiebt sich aus Vergleichung von (4) und (5)
  6. IL : LN = NF : IE = CI : CN nach (1), aber
  • IL : LN = GE : GF und CI : CN = DE : DF, also
  • GE : GF = DE : DF, q.e.d.
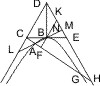  Anderer Beweis. Man ziehe EA, welche CB in O, CD in P trifft, und von B eineParallele mit DF, die PO in Q trifft. Nun ist
  1. BQ : EH = OQ : OE,
  oder weil wegen Gleichheit von AB und AD auch AQ = AE und BQ = DE, EH ferner gleich DF und AO = EP ist:
  2. DE : DF = PE - AE : PA, und das
     PE : AE = DE : GE, auch
  3. DE : DF = DE - GE : DG,
  woraus durch Subtraction der correspondirenden Glieder:
  4. GE : GF = DE : DF. q.e.d.
• 
  Lehrsatz 36. Wenn von einem Punkt in einer Asymptote zweier Gegenschnitte eine Tangente an einen derselben und eine beliebige Gerade, die jeden der Gegenschnitte in einem Punkt trifft, durch den Berührungspunkt der Tangente aber eine Parallele mit der erwähnten Asymptote gezogen werden, so verhalten sich auf der beliebig gezogenen Geraden die beiden Stücke, welche zwischen dem Punkt auf der Asymptote und den Gegenschnitten, wie die beiden, welche zwischen dem Punkt auf der Parallelen mit der Asymptote und den Gegenschnitten liegen.
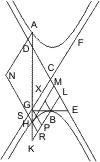  Sei D ein Punkt auf einer Asymptote zweier Gegenschnitte, DA eine Tangente an einen derselben, und eine beliebige Gerade von D gezogen, die die Gegenschnitte in den Punkten E, F und eine von A mit der Asymptote CD gezogene Parallele in G trifft, so wird behauptet:
  • DE : DF = GE : GF.
  Erster Beweis. Man nenne B den Durchschnitt von DA, H den von DF mit der zweiten Asymptote und ziehe von den Punkten E, A, F Parallelen mit den Asymptoten CB, CD, welche diese beziehlich in den Punkten I und K, L und M, N und O treffen. Nun ist wie leicht aus II.12 folgt:
  1. CI · IE = CL · LA = CN · NF, also
  2. CI : CL = LA : IE
  3. CL : CN = NF : LA,
  woraus durch Subtraktion der Glieder eines Verhältnisses in (2), durch Addition in (3) folgt:
  4. IL : IE - AL = CL : IE,
  5. NL : NF + LA = CL : NF.
  Aber IE - AL oder KM ist gleich NF + LA oder MO, weil wegen Gleichheit von DA und AB auch DM = CM und wegen Gleichheit von DE und HF (II.16) auch DK = CO; hiernach ergiebt sich also aus (4) und (5)
  6. IL : NL = NF : IE = CI : CN,
  aber IL : NL = GE : GF und CI : CN = DE : DF, folglich auch
  7. GE : GF = DE : DF. q.e.d.
  Zweiter Beweis. Man ziehe AE, die CB in O, CD in P trifft, schneide AO von AE ab zum Punkt Q, ziehe DQ. Nun ist, weil auch DA = AB, DQ parallel BH, folglich
  1. DE : EH = EQ : EO = AE - EP : AE + EP, weil AO = EP.
  Weil aber AE : EP = GE : DE, ist auch
  • AE - EP : AE + EP = GE - DE : GE + DE, mithin
  2. DE : EH = GE - DE : GE + DE, woraus durch Addition der correspondirenden Glieder
  3. GE : GH + DE = DE : EH, weil aber DB = HF, ist GH + DE = GF und EH = DF, also
  4. GE : GF = DE : DF. q.e.d.
  Dritter Beweis. Man ziehe ausser wie oben AE noch von A eine Parallele mit BC, welche DH in R trifft, so ist, weil DA = AB, auch DR = RH und
  1. ER : RH = EA : AO = EA :EP = GE : DE; aber BR = ½ · EF und RH = · DH, mithin
  2. EF : DH = GE : DE, woraus durch Addition der correspondirenden Glieder unter Berücksichtigung von DE = HF:
  3. GF : D F= GE : DE. q e. d.
• 
  Lehrsatz 37. Wenn von einem Punkt an einen Kegelschnitt oder an zwei Gegenschnitte zwei Tangenten und eine beliebige den Kegelschnitt oder bei Gegenschnitten die eine Hyperbel in zwei Punkten schneidende Gerade gezogen werden, so verhalten sich auf dieser letzteren die beiden Stücke vom Ausgangspunkte bis zu den Durchschnittspunkten mit dem Kegelschnitt wie die beiden Stücke von der Berührungssehne zu denselben Durchschnittspunkten gerechnet.
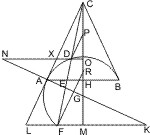
  Sei D ein Punkt ausserhalb eines Kegelschnittes oder zweier Gegenschnitte und seien von ihm aus die Tangenten DA und DB und die schneidende Gerade DEF, welche die Berührungsehne in G trifft, gezogen, so wird behauptet:
  • DE : DF = GE : GF.
  Beweis. Man ziehe die Durchmesser durch A und D und von E und F an letzteren die Ordinaten, welche diesen Durchmesser, die Tangente DA und den durch A gezogenen Durchmesser beziehlich in den Punkten H, I, K und L, M, N treffen, ferner von E und F Parallelen mit der Tangente DA, die CD beziehlieh in O und P treffen. Nun ist:
  1. ∆DIH : ∆DML = DI² : DM² = DE² : DF²,
  2. ∆EHO : ∆ FLP = EH² : FL² = DE² : DF²
  Mithin ∆DJH : ∆DML = ∆EHO :∆FLP = DE² : DF² und deshalb durch Subtraction auch
  3. ∆DIH - ∆EHO : ∆DML - ∆FLP = DE² : DF². Es ist aber ferner
  4. ∆AKI : ∆AMN = AI² : AM² = GE² : GF²
  und da nach III.2 bei einem Kegelschnitt, nach III.5 bei Gegenschnitten ∆AKI = EIDO und ∆AMN = FMDP, erhält man aus Vergleichung von (3) und (4):
  • DE² : DF² = GE² : GF² oder DE : DF = GE : GF. q.e.d.
  Ein in neuerer Zeit üblicher auf III.16 und 18 und sonach mittelbar ebenfalls auf III.3 und III.5 sich stützender Beweis ist folgender: Seien unter denselben Bezeichnungen als oben die Durchschnitte von EH und FL mit dem Kegelschnitt und der Tangente DB beziehlich Q, R und S, T genannt, so ist, weil DC die Linie AB halbirt, auch HI = HR und HE = HQ, mithin IQ = ER und aus ähnlichen Gründen MS = FT. Nun ist nach III.16 bei einem Kegelschnitt, nach III.18 bei Gegenschnitten
  1. AI² : AM² = IE · IQ : MF · MS = IE · ER : MF · FT.
  Da aber IE : MF = DE : DF und auch ER : FT = DE : DF, ist
  2. IE ·ER : MF · FT = DE : DF² und da endlich
  3. AI : AM = GE : GF, folgt durch Vergleichung von (1) mit (2) und (3):
  • GE² : GF² = DE² : DF² oder GE : GF = DE : DF. q.e.d.
• 
  Lehrsatz 38. Wenn von einem Punkt an einen Kegelschnitt oder an zwei Gegenschnitte die beiden Tangenten, von der Mitte der so entstandenen Berührungssehne aber eine beliebige den Kegelschnitt oder bei Gegenschnitten die eine Hyperbel in zwei Punkten schneidende Gerade gezogen werden, so verhalten sich auf dieser die beiden Stücke von ihrem Ausgangspunkt bis zu den Kegelschnittspunkten wie die beiden Stücke zwischen einer durch den Ausgangspunkt der Tangenten mit der Berührungssehne gezogenen Parallelen und den Kegelschnittspunkten.
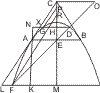  Seien von einem Punkt D an einen Kegelschnitt oder an zwei Gegenschnitte die Tangenten DA, DB und von der Mitte G der Berührungssehne AB eine beliebige den Kegelschnitt in E, F und eine durch D mit AB gezogene Parallele in R schneidende Gerade gezogen, so wird behauptet:
  • GE : GF = RE : RF.
  Man ziehe noch die Durchmesser durch D und A, von E und F an ersteren die Ordinaten, welche die Durchmesser durch D, die Tangente DA und den Durchmesser in A beziehlich in den Punkten H, I, K und L, M, N treffen, ferner von E und F Parallelen mit DA, welche den Durchmesser von D in O und P treffen. Nun ist:
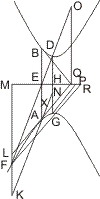
  1. ∆:DIR : ∆DML = DI² : DM² = RE² : RF²,
  2. ∆EHO : ∆FLP = HE² : FL² = HG² : GL² = AI² : AM²,
  3. ∆AKI : ∆AMN = AI² : AM³, also
  4. ∆EHO ± ∆AKI : ∆FLP ± ∆AMN = AI² : AM² = GE² : GF², aber
     ∆EHO ± ∆AKI = ∆DIH und ∆AMN ± ∆LFP = ∆DML
  nach (III.2 und 5), wobei das obere Zeichen in Fig. 184 und 185, das untere in Fig. 186 zu nehmen ist, und folglich aus Vergleichung von (1) und (4):
  • RE² : RF² = GE² : GF² oder RE : RF = GE :GF. q.e.d.
• 
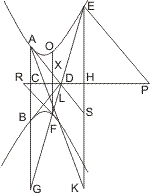  Lehrsatz 39. Wenn von einem Punkt ausserhalb des Asymptotenwinkels an zwei Gegenschnitte die Tangenten und eine beliebige Gerade, welche sowohl jeden der Gegenschnitte als die Berührungssehne in einem Punkt schneidet, gezogen werden, so verhalten sich auf dieser Geraden die Stücke vom Ausgangspunkt bis zu den beiden Punkten auf den Gegenschnitten wie die beiden Stücke von der Berührungssehne bis zu denselben Punkten gerechnet.
  Die Construction und der Beweis dieses Satzes können an der Fig. 187. buchstäblich wie bei § 37 geführt werden.
• 
  Lehrsatz 40. Wenn von einem Punkt ausserhalb des Asymptotenwinkels an zwei Gegenschnitte Tangenten und von der Mitte der so entstandenen Berührungssehne eine beliebige Gerade gezogen werden, welche sowohl jeden der Gegenschnitte als auch die vom Ausgangspunkt der Tangenten mit der Berührungssehne gezogene Parallele in einem Punkt schneidet, so verhalten .sich auf dieser Geraden die beiden Stücke von der Berührungssehne bis zu den Kegelschnittspunkten wie die beiden von der Parallelen mit der Berührungssehne bis zu denselben Punkten gerechnet.
  Die Construction und der Beweis dieses Satzes kann an Fig. 188 buchstäblich wie in § 38 geführt werden.
  Es wäre daher leicht möglich gewesen, die Lehrsätze 37 und 39, 38 und 40 zu vereinigen, indess ist dies im Anschluss an Apollonius und auch deshalb nicht geschehen, weil wegen der Verschiedenheit der Figuren es gut ist, dieselbe Eigenschaft in verschiedenen Fällen zu betrachten.
• 
  Lehrsatz 41. Drei Tangenten einer Parabel theilen sich so, dass aus ihren Stücken sich drei gleiche Verhältnisse bilden lassen.
  Beweis des Apollonius. Seien DA, DB zwei Tangenten einer Parabel, die dritte aber in dem Punkt I gezogen, wo der von D gezogene Durchmesser die Parabel trifft; sind nun K, L die Durchschnittspunkte der dritten Tangente mit DA, DB, H der von DI mit AB, so ist, weil DI = IH (I.35) und KL parallel AB ist, auch DK = KA, DL = LB und weil AH = HB (II.30), auch KI = IL, mithin AK : KD = DL : LB = KI : IL. q.e.d.
  Sei nun aber die dritte Tangente in einem andern Punkt E zwischen I und A gezogen und treffe DA, DB in F und G, so ist zu beweisen:
  • AF : FD = DG : GB = FE : EG.
  Man ziehe durch E den Durchmesser, welcher DA, DB AB beziehlieh in M, N, O trifft und von A und B an diesen Durchmesser die Parallelen AP, BQ mit FG. Nun ist:
  • ME = EP (I.35), also AF = FM und
  1. AF : AK = 2 · AF : 2 · AK = AM : AD = AO : AH,
  • oder wenn man die Hinterglieder verdoppelt:
  2. AF : AD = AO : AB und folglich
  3. AF : FD = AO : OB.
  • Auf dieselbe Weise ist NE = EQ (I.35), also NG = GB und
  4. BG : BL = 2 · BG : 2 · BL = BN : BD = BO : BH,
  • oder wenn man die Hinterglieder verdoppelt:
  5. BG : BD = BO : BA und also
  6. BG : GD = BO : OA.
  • Endlich ist:
  7. AO : BO = AP : BQ = 2 · FE : 2 · GE = FE : GE;
  • mithin aus Vergleichung von (3), (6), (7):
  • AF : FD = DG : BG = FE : EG. q.e.d.
  Ein in neuerer Zeit üblicher Beweis ist folgender:
  Seien unter Beibehaltung obiger Bezeichnungen von den Punkten E, F, G Durchmesser gezogen, die AB beziehlieh in R, S, T treffen und seien U, V die Durchschnittspunkte von FS mit AE und von GT mit BE.
  Nun ist AH = HB, AU = UE, BV = VE nach (II.30), also auch AS = SR, BT = TR; da nun AR + RB = 2 · AB + 2 · BT = AB, ist AS + BT = AH und folglich BT = SH und AS = TH, also selbstverständlich AS : SH = HT : TB = SR : RT und folglich auch AF : FD = DG : GB = FE : EG. q.e.d.
• 
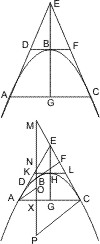
  Lehrsatz 42. Wenn zwei parallele Tangenten einer Ellipse oder zweier Gegenschnitte von einer dritten durchschnitten werden, so ist das Rechteck aus den Stücken, welche auf ihnen abgeschnitten werden, gleich dem Quadrat des halben Durchmessers, der mit ihnen parallel ist.
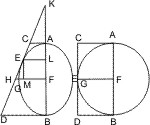  Seien in den Endpunkten A und B des Durchmessers einer Ellipse oder zweier Gegenschnitte Tangenten gezogen, welche von einer dritten, deren Berührungspunkt E ist, in den Punkten F und G geschnitten werden, und sei CD ein mit AF oder BG paralleler Halbmesser, so ist zu beweisen:
  • AF · BG = CD².
  Beweis. Man ziehe von E an AB und CD die Ordinaten EI und EL und nenne H und K die Durchschnittspunkte von GF mit den verlängerten AB, CD. Nun ist nach I.37:
  1. CI : CA = CA : CH, also auch
  2. AI : HA = CB : CH, woraus ferner
  3. HA : HI = HC : HB, also auch
  4. AF : EI = CK : BG oder AF · BG = EI · CK = CL · CK,
  • aber nach I.38 CL · CK = CD² und folglich AF · BG = CD². q.e.d.
• 
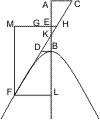
  Lehrsatz 43. Werden an eine Hyperbel zwei Tangenten gezogen, so ist das Rechteck aus den Abschnitten, welche die eine auf den Asymptoten bildet, gleich dem Rechteck aus den Abschnitten, die die andere Tangente bildet.
  Seien in den Punkten A und B einer Hyperbel Tangenten gezogen, deren erstere die Asymptoten in den Punkten D und E, letztere in den Punkten F und G trifft, so ist zu beweisen, dass
  • CD · CE = CF · CG.
  Man ziehe von A und B Parallelen AH, BI mit der einen Asymptote CD bis an die andere CE, so ist nach II.12 CH · HA = CI · IB und aa nach II.3 DA = AE und FB = BG, ist CE = 2 · CH, CD = 2 · AH, CG = 2 · CI, CF = 2 · BI, also CD · CE = 4 · CH · AH und CF · CG = 4 · CI · IB, mithin CD · CE = CF · CG. q.e.d.
• 
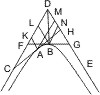
  Lehrsatz 44. Wenn zwei Tangenten einer Hyperbel oder zweier Gegenschnitte die Asymptoten treffen, so ist die Berührungssehne parallel den beiden Linien, welche die Durchschnittspunkte der Tangenten mit den Asymptoten verbinden.
  Seien in den Punkten A und B einer Hyperbel oder zweier Gegenschnitte Tangenten gezogen, welche die Asymptoten in den Punkten D und E, F und G treffen, so wird behauptet:
  • AB ∥ FE ∥ DG.
  Beweis. Es ist nach vorigem Satz CD · CE = CF · CG (was auch bei Gegenschnitten leicht nachzuweisen), folglich FE parallel DG, und da A die Mitte von DE, B von FG nach I.3, ist auch AB ∥ FE ∥ DG. q.e.d.
• 
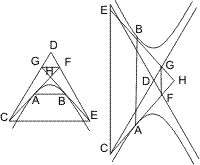
  Lehrsatz 45. Wenn in den Endpunkten der Achse einer Ellipse oder zweier Gegenschnitte Tangenten gezogen und von einer beliebigen dritten Tangente durchschnitten werden, und wenn in der Achse auf jeder Seite ein Punkt bestimmt wird, so dass das Rechteck der Abschnitte, die er bildet, gleich dem Quadrat der halben kleinen Achse ist (und zwar muss bei der Ellipse jeder der so bestimmten Punkte innerhalb der Achse, bei Gegenschnitten in ihrer Verlängerung liegen), so schliessen die Linien, welche von einem so bestimmten Achsenpunkt nach den beiden Durchschnittspunkten der dritten Tangente mit den beiden ersten Tangenten gezogen werden; einen rechten Winkel ein.
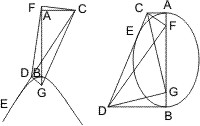  Sei AB die Achse einer Ellipse oder zweier Gegenschnitte und seien die Tangenten in A und B von einer dritten in D gezogenen in den Punkten E und F durchschnitten, sei ferner S ein Punkt zwischen A und B bei der Ellipse, ausserhalb AB bei der Hyperbel, so dass AS · BS = dem Quadrat der halben kleinen Achse ist, so wird behauptet, dass
  • ∠ESF = 1 Rechten.
  Beweis. Nach III.42 ist AE · BF gleich dem Quadrat der halben kleinen Achse, also AE · BF = AS · BS und ∆AES ähnlich dem ∆BSF, also ∠ESA = ∠BFS und da ∠BFS + BSF = 1 R, auch ∠ESA + ∠BSF = 1 R, mithin auch ∠ESF = 1 R. q.e.d.
  Erklärung. Die beiden auf die beschriebene Art in der Achse zu bestimmenden Punkte heissen die Brennpunkte.
• 
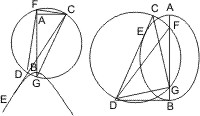  Lehrsatz 46. Wird übrigens unter denselben Voraussetzungen als im vorigen Satz der Schneidungspunkt der dritten Tangente und einer der beiden parallelen mit den beiden Brennpunkten verbunden, so machen diese beiden Verbindungslinien gleiche Winkel mit den in diesem Schneidungspunkt zusammenstossenden Tangenten.
  Sei H der zweite Brennpunkt, so liegen, weil ESF und EHF nach vorigem Satz rechte Winkel sind, die vier Punkte E, F, S, H in einem Halbkreis, mithin ist ∠FEH = ∠FSH als Peripheriewinkel auf demselben Bogen, ∠FSH aber = ∠SEA nach vorigem Beweis, also ∠FEH = ∠SEA. q.e.d.
• 
  Lehrsatz 47. Werden unter denselben Voraussetzungen als in den vorigen Lehrsätzen die Durchschnittspunkte der dritten Tangente mit den in den Endpunkten der Achse gezogenen mit beiden Brennpunkten verbunden, so steht die Linie von einem der durch diese Verbindungslinien erhaltenen Kreuzungspunkte nach dem Berührungspunkt der dritten Tangente senkrecht auf dieser.
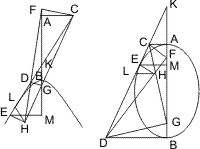  Sei übrigens unter denselben Bezeichnungen als oben I der Kreuzungspunkt von FS und EH, so ist zu beweisen, dass
  • ID lothrecht auf EF steht.
  Wäre eine andere Linie IL lothrecht, so hätte man ∆FIL ähnlich ∆FBH und ∆EIL ähnlich ESA, ferner ∆FHI ähnlich ∆ESI, wie leicht aus den zuletzt bewiesenen Sätzen folgt, sonach
  1. FL : FB = FI : FH = EI : ES = EL : EA
  oder wenn man im ersten und letzten Verhältniss die innern Glieder vertauscht:
  2. FL : EL = FB : EA;
  aber nach einer leichten Folgerung aus III.16 ist:
  • FD : ED = FB : EA,
  was der vorigen Proportion widerspricht, und es ist also unmöglich, dass eine andere Linie ausser ID Iothrecht auf EF steht, mithin ID Iothrecht auf EF. q.e.d.
• 
  Lehrsatz 48. Die Linien vom Berührungspunkt einer Tangente nach den Brennpunkten gezogen, bilden gleiche Winkel mit der Tangente.
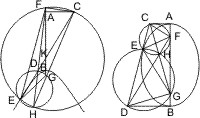  Seien unter Beibehaltung der obigen Bezeichnungen noch SD und HD gezogen, so wird behauptet:
  • ∠SDE = ∠HDF.
  Weil IDE = ISE = 1 Rechten nach den vorigen Sätzen, liegen die Punkte S, I, D, E in einem Kreis, und weil ∠IDF = ∠IHF = 1 Rechten, auch die Punkte H, I, D, F; folglich ist:
  1. ∠EDS = ∠EIS und ∠FDH = ∠FIH
  bei der Ellipse oder = ∠EIS bei der Hyperbel als Peripheriewinkel, aber ∠EIS = ∠FIH und also in jedem Fall ∠SDE = ∠HDF. q.e.d.
• 
  Lehrsatz 49. Wird von einem Brennpunkt auf eine Tangente ein Loth gefällt, so schliessen die Linien vom Fusspunkt desselben nach den Endpunkten der Achse einen rechten Winkel ein.
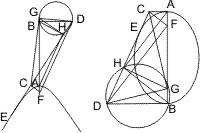  Sei unter Beibehaltung obiger Bezeichnungen HK ein Loth von H auf EF gefällt und KA, KB gezogen, so ist zu zeigen, dass:
  • ∠AKB = 1 Rechten.
  Die Punkte F, K, H, B liegen in einem Kreise, weil ∠FKH und ∠FBH rechte Winkel sind, aus ähnlichen Gründen die Punkte E, K, H, A. Also ist ∠HKB = ∠HFB = ∠EHA und ∠HKA = ∠HEA als Peripheriewinkel; da aber ∠EHA + ∠HEA = 1 Rechten, muss auch ∠HKB + ∠HKA = 1 Rechten. q.e.d.
• 
  Lehrsatz 50. Ist der Berührungspunkt einer Tangente mit einem Brennpunkt verbunden, und zieht man mit dieser Verbindungslinie eine Parallele vom Mittelpunkt bis an die Tangente, so ist diese Parallele gleich der halben Achse.
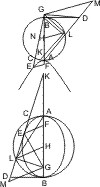  Man ziehe unter Beibehaltung der obigen Bezeichnungen vom Mittelpunkt C mit SD eine Parallele CK bis an die Tangente EF, so ist zu zeigen, dass
  • CK = ½ · AB.
  Zieht man noch von H die Parallele HN mit SD bis an dieselbe Tangente und verbindet H mit K, so ist, weil SC = HC, auch DK = KN, und weil ∠EDS = ∠KNH als correspondirender oder Wechselwinkel und gleich ∠HDN nach § 48, ist auch ∠KNH = ∠HDK, folglich HK senkrecht auf EF und deshalb nach vorigem Satze BKA = 1 Rechten, mithin CK = ½ · AB. q.e.d.
• 
  Lehrsatz 51. Werden in einer Hyperbel oder in zwei Gegenschnitten von den Brennpunkten nach einem beliebigen Punkt des Kegelschnitts Linien gezogen, so ist deren Unterschied gleich der Achse.
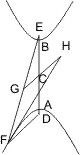  Seien bei einer Hyperbel oder zwei Gegenschnitten AB die Achse S, H die Brennpunkte, D ein beliebiger Punkt im Umfang, so ist zu zeigen, dass HD - SD = AB.
  Man ziehe in D die Tangente und durch C eine Parallele mit SD, die die Tangente in K, HD in O schneidet, so ist, weil ∠ODK = ∠SDK (nach § 48), auch ∠OKD = ∠ODK und folglich OK = OD oder OK = ½ · HD; da aber OK = OC + CK und OC = ½ · SD so wie CK = ½ · AB (§ 50), so hat man ½ · SD + ½ · AB = ½ · HD oder AB = HD - SD. q.e.d.
• 
  Lehrsatz 52. Wenn von den beiden Brennpunkten einer Ellipse an einen beliebigen Punkt des Umfangs Linien gezogen werden, so ist deren Summe gleich der Achse.
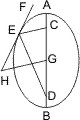  Seien AB die Achse, S, H die Brennpunkte, D ein beliebiger Punkt im Umfang einer Ellipse, so ist zu beweisen, dass HD + SD = AB.
  Man ziehe in D die Tangente EF und von C eine Parallele mit SD, die die Tangente in K, HD in O trifft, so ist, weil ∠EDS = ∠FDH (nach § 48), auch ∠OKD = ∠ODK, mithin OD = OK oder ½ · HD = OK, aber OK = CK - CO und da CK = ½ · AB (nach § 50) und CO = ½ · SD, erhält man ½ · AB - ½ · HD = ½ · SD oder HD + SD = AB. q.e.d.
• 
  Lehrsatz 53. Wenn in einer Ellipse, Hyperbel oder in zwei Gegenschnitten von den Endpunkten eines Durchmessers nach einem beliebigen Punkt des Kegelschnitts Linien gezogen werden, welche entweder selbst oder in ihrer Verlängerung die in den Endpunkten des Durchmessers gezogenen Tangenten schneiden, so ist das Rechteck aus den auf den Tangenten abgeschnittenen Stücken gleich dem Quadrat des zu dem vorerwähnten zugehörigen conjugirten Durchmessers.
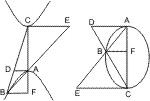  Seien in einer Ellipse, Hyperbel oder in zwei Gegenschnitten von den Endpunkten A, B eines Durchmessers nach dem beliebigen Punkt E des Umfangs die Linien AE, BE gezogen, welche die in B und A gezogenen Tangenten in den Punkten F und G treffen, und sei DI der zu AB gebörige conjugirte Durchmesser, so wird behauptet:
  • AG · BF = DI².
  Man ziehe von E an AB die Ordinate EH, so ist
  1. AG : EH = AB : BH,
  2. BF : EH = AB : AH, also
  3. AG · BF : EH² = AB² : BH · AH oder
  • AG · BF : AB² = EH² : BH · AH = DI² : AB² (I.21).
  Da also das zweite Glied gleich dem vierten ist, muss auch AG · BF = DI². q.e.d.
• 
  Lehrsatz 54. Wenn von einem Punkt ausserhalb einer Ellipse, Hyperbel oder Parabel Tangenten an diese, von den beiden Berührungspunkten aber Parallelen mit diesen Tangenten so wie ;Linien nach einem beliebigen Punkt des Kegelschnitts gezogen werden, welche entweder selbst oder in ihrer Verlängerung die mit den Tangenten gezogenen Parallelen schneiden, so ist das Verhältniss des Rechtecks aus den auf diesen Parallelen abgeschnittenen Stücken zum Quadrat der Berührungssehne zusammengesetzt ans dem Verhältniss der Quadrate der beiden Stücke, welche auf der von er Mitte der Berührungssehne nach dem Ausgangspunkt der Tangenten gehenden Linie zwischen dieser Mitte und einem Kegelschnittspunkt und zwischen diesem Punkt und dem Ausgangspunkt der Tangenten liegen, und aus dem Verhältniss des Rechtecks der Tangenten zum Quadrat der halben Berührungssehne.
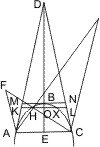  Seien von einem Punkte D an eine Ellipse, Hyperbel oder Parabel die Tangenten DA, DB, von A und B aber Parallelen mit DB, DA so wie Linien nach einem beliebigen Punkt E im Kegelschnitt gezogen, welche den Parallelen beziehlieh in F, G begegnen, so ist, wenn H die Mitte von AB, I der Durchschnitt von DH mit dem Kegelschnitt ist, zu beweisen:
  • AG · BF : AB² = HI² · AD · BH : DI² · AH²
  Beweis. Man ziehe noch von E und I Parallelen mit AB, deren erstere den Kegelschnitt zum zweiten Mal in K, die Linien DA, DB, DH beziehlich in L, M, N, deren letztere DA, DB in O und P trifft, so ist ∆GAB ähnlich ∆BME, ∆FBA ähnlich ∆ALE, also
  1. AG : AB = BM : ME,
  2. BF : AB = AL : LE, mithin
  3. AG · BF : AB² = BM · AL : ME ·LE = BM ·AL² : ME · LE ·AL
  und da, wie leicht zu zeigen ME = LK und nach III.16 AL² : LK · LE = AO² : OI², erhalten wir
  4. AG · BF : AB² = BM · AO² : AL · OI²
     = BD · AO² : AD ·OI²
     = AD · BD · AO² : AD² · OI².
     = AD · BD · IH² : DH² · OI².
  Weil aber endlich AH : OI = DH : DI oder DH · OI = AH · DI, erhalten wir
  5. AG · BF : AB² = HI² · AD · BD : DI² · AH². q.e.d.
• 
  Lehrsatz 55. Wenn von einem Punkte ausserhalb des Asymptotenwinkels in zwei Gegenschnitten Ta genten an diese und von den Berührungspunkten Parallelen mit diesen Tangenten sowie Linien nach einem beliebigen Punkt eines der beiden Gegenschnitte gezogen werden, welche entweder selbst oder verlängert die Parallelen schneiden, so verhält sieh das Rechteck aus den auf den Parallelen abgeschnittenen Stücken zum Quadrat der Berührungssehne wie das Rechteck aus den Tangenten zum Quadrat der von ihrem Ausgangspunkt bis an einen der Gegenschnitte gezogenen Parallelen mit der Berührungssehne.
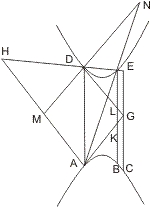  Seien vom Punkt D ausserhalb des Asymptotenwinkels zweier Gegenschnitte an diese die Tangenten DA, DB, von A und B Parallelen mit DB, DA und Linien nach einem beliebigen Punkt E eines der beiden Kegelschnitte gezogen, die die von B und A gezogenen Parallelen beziehlich in F und G treffen, so ist, wenn DR eine von D bis an einen der beiden Gegenschnitte gezogenen Parallele mit AB ist, zu beweisen, dass
  • AG · BF : AB² = AD · BD : DR²,
  Beweis. Man ziehe noch durch E eine Parallele mit AB, die den andern Gegenschnitt in K, die Tangenten DA, DB in L, M trifft, so ist ∆GAB ähnlich dem ∆BME und ∆FBA ähnlich dem ∆ALE, mithin
  1. AG : AB = BM : ME,
  2. BF : AB = AL : LE, also
  3. AG · BF : AB² = BM · AL : LE · ME =
     = BM · AL² : LE · ME · AL
  und da AL² : LE · ME = AD² : DR² nach III.20 und BM : AL = BD : AD, erhält man
  4. AG · BF  AB² = BD · AD² DR² · AD = BD · AD DR². q.e.d.
• 
  Lehrsatz 56. Wenn von einem Punkt innerhalb des Asymptotenwinkels an eine Hyperbel zwei Tangenten, von den Berührungspunkten aber Parallelen mit diesen Tangenten und Linien nach einem beliebigen Punkt des zugehörigen andern Gegenschnitts gezogen werden, welche diese Parallelen schneiden, so ist das Verhältniss des Rechtecks aus den auf den Parallelen entstandenen Abschnitten zum Quadrat der Berührungssehne zusammengesetzt aus dem Verhältnies der Quadrate der beiden Stücke des durch den Ausgangspunkt der Tangenten gehenden Durchmessers, welche zwischen der Mitte der Berührungssehne und dem andern Gegenschnitt und zwischen diesem Gegenschnitt und dem Ausgangspunkt der Tangenten liegen und aus dem Verhältniss des Rechtecks der Tangenten zum Quadrat der halben Berührungssehne.
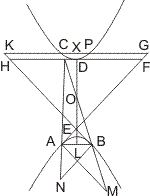  Seien von einem Punkte D innerhalb des Asymptotenwinkels zweier Gegenschnitte Tangenten DA, DB an die eine Hyperbel, und von A und B Parallelen mit DB, DA so wie Linien nach einem beliebigen Punkt E des andern Gegenschnitts gezogen, welche den Parallelen beziehlich in F und G begegnen, so ist, wenn H die Mitte von AB, I der Durchschnitt von DH mit dem zweiten Gegenschnitt ist, zu beweisen:
  • AG · BF : AB² = HI² · AD · BD : DI² · AH².
  Beweis. Man ziehe noch durch E und I Parallelen mit B, deren erstere den Gegenschnitt zum zweiten Mal in K, die Tangenten DA, DB in L, M und DH in N, deren letztere DA und DB in O und P trifft, so ist, weil ∆GAB ähnlich ∆BME und ∆FBA ähnlich ∆ALE,
  1. AG : AB = BM : ME,
  2. BF : AB = AL : LE, also
  3. AG · BF : AB² = AL · BM : LE · ME =
     = AL² · BM : ME ·LE · AL.
  Es ist aber ME = LK und nach III.18
  • AL² : LK · LE = AO² : OI², und da ausserdem
  • BM : AL = BD : AD, erhält man
  4. AG · BF : AB² = AO²2 · BD : OI² · AD = AO² ·BD · AD : OI² · AD²,
  und da AO : AD = HI : DH
  5. AG · BF : AB² = HI² · AD · BD : OI² · DI².
  Weil aber endlich OI : AH = DI : DH, ist OI² · DH² = DI² · AH², mithin
  6. AG · BF : AB² = HI² · AD · BD : DP · AH². q.e.d.
  Anm. Es ist leicht zu erkennen, dass in diesen letzten vier Lehrsätzen des dritten Buchs der Keim der Lehre von der Erzeugung der Kegelschnitte durch projektivische Gerade und Strahlbüschel enthalten ist; denn das constante Rechteck AG · BF macht die Geraden, auf denen es von den festen Punkten A und B aus abgeschnitten wird, nach Steinerscher Bezeichnung zu projektivisch ähnlichen Geraden, mit welchen die Strahlbüschel bei B und A perspektivisch sind, diese Strahlbüschel sind also unter sich projektivisch schief und erzeugen deshalb einen Kegelschnitt. Da ferner, sobald die Geraden AG, BF mit den festen Punkten A und B und die Grösse des constanten Rechtecks AG · BP gegeben sind, auch AD, BD, AB, AH bekannt sind, so st sogleich das Verhältniss HI :  DI gegeben und somit ein Weg angedeutet, .wie aus zwei in schiefer Lage gegebenen projektivischen Strahlbüscheln alsbald der Mittelpunkt und ein Paar conjugirter Durchmesser des dadurch bestimmten Kegelschnitts gefunden werden können; denn theilt man die Gerade HD nach dem gegebenen Verhältniss HI :  DI, so sind die beiden Theilungspunkte die Durchschnittspunkte des Durchmessers DH mit dem Kegelschnitt, die Mitte zwischen ihnen der Mittelpunkt und DH, AB die Richtungen eines Paars conjugirter Durchmesser.