Erläuterungen zu Keplers Liber V, Pars Prima, De figura orbitae

Im Abschnitt "Zeige, was diese elliptischen Größen in der Planetenbahn repräsentieren und welche von ihnen aus der Libration resultieren." erläutert Kepler die Parameter der elliptischen Planetenbahn und führt dazu eine Abbildung ein. Er zeichnet einen Kreis [mit dem Durchmesser der großen Ellipsenachse 2·a], dessen Mittelpunkt mit dem der eingeschriebenen Ellipse zusammenfält und er diskutiert nun die grundlegenden geometrischen Zusammenhänge.

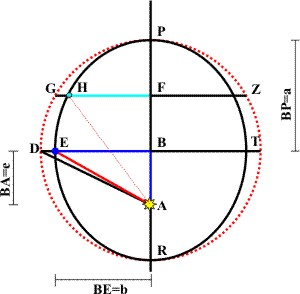
Die Ellipse hat BP als die große Halbachse a und die auf dieser senkrechtstehende Sehne DT, auf der die kleine Halbachse b vom Mittelpunkt B nach E abgetragen ist. Die [lineare] Exzentrizität e ist die Strecke AB vom Brennpunkt A zum Mittelpunkt B. Sie entspricht der Hälfte der Libration — das ist also der Abstand der beiden Brennpunkte A und F (dass F der zweite Brennpunkt ist,hat Kepler im vorangeganenen Abschnitt erwähnt).

Steht nun der Planet in E, d. h. er hat vom Scheitel P 90° seines vollständigen Umlaufes zurückgelegt: d. h. er steht im "ersten Quadranten". Dort ist er nun weniger weit von der Sonne A entfernt als er es zu Beginn des Umlaufes in P war. Seine Entfernung von der Sonne entspricht in E der Länge der großen Halbachse a, in P war er a + e.

Nun betrachtet Kepler einen Planeten, der statt eines Quadranten nur einen Kreisbogen PG weit vom Aphel P (sonnenferner Scheitel der Ellipse) gewandert ist, und zeigt, wie man die zugehörigen Entfernung von der Sonne ermittelt. Der Schnittpunkt der Entfernung mit der Sehne GZ ist der Punkt H. Da F der zweite Brennpunkt ist, ist die Strecke HF der halbe Ellipsenparameter p.

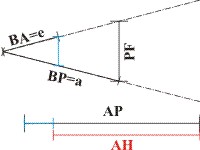Nach der vorangegangenen Argumentation sucht er also eine Strecke (hier blau), die sich zu der zum Kreisbogen PG entsprechende Strecke PF verhält, wie die lineare Exzentrizität zur großen Halbachse der Ellipse. Er sucht also die Länge der Strecke PX im vorangegangenen Abschnitt.
Dazu konstruiert er ein gleichseitiges Dreieck mit der Basislänge PF und den Schenkellängen BP = a. Dann sucht er die Schenkellänge, die zur Basis PF gehört. Diese blaue Strecke zieht er vom Abstand des Aphels P von der Sonne ab und erhält die Strecke AH. (Die Verwendung dieses "Proportionalzirkels" wird ausführlich bei Edmund Gunter in den Büchern zum Sector erläutert.)

Damit hat Kepler zwei Punkte der elliptischen Bahn gefunden. Er bezieht sich nun auf die Regel des Apollonius von Perga, wonach sich die Abschnitte gemeinsamer Sehnen von Ellipse und Umkreis verhalten wie die kleine zur großen Halbachse der Ellipse. Dann konstruiert er ein Gnomon.

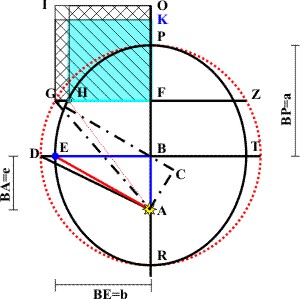Er zeichnet die Quadrate über der Strecke GF (schraffiert) und über HF (blau). Dann verbindet er den Kreispunkt G mit dem Brennpunkt A und dem Mittelpunkt B. Auf der verlängerten Ver­bin­dungs­linie GA errichtet er das Lot AC durch den Brennpunkt A.
Nun ist das Quadrat über der Seite AC gleich dem Gnomon HIK, das ist die Summe der Flächen der beiden kreuz­schraf­fierten Recht­ecke plus der des kleinen Quadrats oben links. Es folgt der Beweis.
Wie vorher dar­gestellt, verhält sich BP = a zu PF wie BA = e zur Differenz der Strecken AP und AH und BA = e und es verhalten sich BA = e zur Differenz von AH und BP = a, wegen der Kon­struk­tion von AH (siehe oben). Und es gilt: wie sich PB = GB = a zu BF verhält, so verhält AB = e zu BC, weil die recht­winkligen Dreiecke GFB und ACB einen gemein­samen Scheitel­winkel haben. (Die Scheitel­winkel sind in beiden Dreiecken gleich, der zweite Winkel hat 90°, und da die Summe der Winkel im Dreieck 180° beträgt, muss auch der dritte Winkel in beiden Dreiecken gleich sein, also sind die ent­spre­chen­den Seitenverhältnisse gleich.)

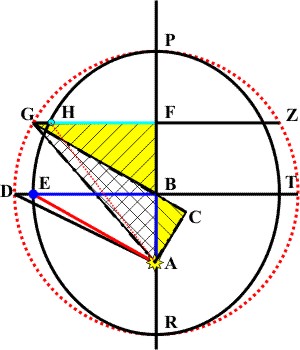Nun ist BC gleich dem Anteil, um den der Abstand AH des Planeten von der Sonne die große Halbachse BP = a übersteigt. Und es folgt, dass GC und HA gleich lang sind. Jetzt wendet Kepler den Satz des Pythagoras an auf die rechtwinkligen Dreiecke GCA (schraffiert) und GFA (schraffiert), die die Seite AG gemeinsam haben.
GF² + FA² = GA²
AC² + GC² = GA²
FA² + FH² = AH²
Die letzte Gleichung löst man nach FA² auf und setzt in die erste ein:
GF² + AH² - FH² = AC² + GC² oder
GF² - FH² = AC² + GC² - AH²
die mittlere Gleichung löst man nach GC² auf und setzt in die vorige ein:
GF² - FH² = GA² - AH².
Die linke Seite der Gleichung ist in dem Gnomon der obigen Abbildung die schraffierte, ungefärbte Restfläche, die rechte Seite die Differenz der Quadrate der Entfernungen des Kreispunktes G und des Ellipsenpunktes H vom Brennpunkt A. Das Gnomon ist somit ein Maß für diesen Unterschied.

Damit ist gezeigt, dass sich alle Sehnenabschnitte wie die zugehörigen Lote AC verhalten. Und es verhalten sich die Abstände vom Brennpunkt zu einem Punkt auf dem Kreis und einem Punkt auf der Ellipse, die beide auf einer Sehne senkrecht zur Apsidenlinie liegen, wie die große zur kleinen Halbachse der Ellipse.

Man erkennt auch unschwer, dass das kleine Quadrat des Gnomons die Seitenlänge hat, die der Differenz der Kreis- und Ellipsensehnenabschnitte entspricht. Kepler kann damit den Abstand eines Planeten auf der elliptischen Bahn von der Sonne in Abhängigkeit von einem Kreisbogen zwischen Aphel und aktuellem Ort berechnen.