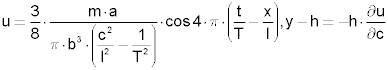Ebbe und Flut
aus: Felix Auerbach: Wellenbewegung in Flüssigkeiten
Übersicht. Mit dem Ausdruck Gezeiten oder Tiden oder "Ebbe und Flut" bezeichnet man diejenigen Schwankungen des Meeresspiegels, die regelmäßigen, wenn auch kompliziert periodischen Charakters sind und die man als eine Folge astronomischer Einflüsse erkannt hat; es kommen aber sekundär auch terrestrische Einflüsse hinzu, deren Wirkungen man, soweit sie sich mit den astronomischen zu einheitlichen Phänomenen kombinieren, mit hinzunehmen muß.
Das Gezeitenphänomen ist von großer Komplikation im einzelnen, es lassen sich aber folgende Grundtatsachen herausschälen. Das Meeresniveau unterliegt einem periodischen Steigen und Fallen, und zwar mit einer durchschnittlichen Periode von 12 Stunden und 25 Minuten — der Zusammenhang mit dem Monde, der jeden Tag 50 Minuten später durch den Meridian geht, ist einleuchtend, zugleich aber auch der Umstand, daß auf eine Mondstellungsperiode zwei Gezeitenperioden kommen. Die Phasen beider Vorgänge fallen jedoch im allgemeinen nicht zusammen, ihre Differenz ändert sich mit der Phase des Mondes.
Das Maximum heißt Hochwasser oder Flut, das Minimum Tiefwasser oder Ebbe; die Worte Flut und Ebbe werden jedoch auch in anderem Sinne, nämlich für den Vorgang des Steigens bezw. Fallens gebraucht. Ferner wechselt die Amplitude periodisch, das Maximum der Flut heißt Springflut, das Minimum Nippflut; jene in erster Annäherung zur Zeit von Voll- oder Neumond, diese zur Zeit des ersten oder letzten Viertels; auf eine Mondbahnperiode entfallen also wiederum zwei Gezeitenperioden; auch hier aber gibt es wiederum eine gewisse wechselnde Phasendifferenz. — An verschiedenen Orten herrschen gleichzeitig verschiedene Phasen, ihre Differenz hängt in erster Reihe von der geographischen Länge der Orte ab; in zweiter Reihe kommt aber für die Phase auch die geographische Breite, in dritter, besonders für Küstenorte und ganz besonders für Orte an Buchten, Vorgebirgen, Inseln u. s. w. die geographische Konfiguration in Betracht. Die durch diese Faktoren bedingte, in wahrer, astronomischer Ortszeit ausgedrückte Zeit des Hochwassers eines Ortes nach Voll- oder Neumond heißt seine Hafenzeit. — Die Verschiedenheit des Niveaus an verschiedenen Orten ruft Strömungen hervor, die man als Flutströmung oder, da sie ebenfalls periodischen Charakters ist, als Flutwelle bezeichnet. Der Verlauf der Flutwellen wird hiernach ebenfalls ganz wesentlich durch die Konfiguration von Wasser und Land bestimmt. Das aber hat wiederum eine Rückwirkung auf die Fluthöhe, die hiernach ebenfalls an verschiedenen Orten sehr verschieden ausfällt. — Schließlich haben meteorologische Faktoren unter Umstanden erheblichen Einfluß auf die Gezeiten, namentlich Luftbewegungen.
Im folgenden soll die Theorie, die Beobachtung und der Verlauf der Gezeiten ganz kurz skizziert werden; wegen des genaueren, das in die Geophysik gehört, sei auf die Hand- und Lehrbücher von Günther, Darwin, Bogus-Lawski-Krámmel, sowie auf die Journale, besonders die Annalen der Hydrographie und ihre Annexe, verwiesen.
Gleichgewichtstheorie. Diese schon von Newton ausgearbeitete Theorie wird zwar den tatsächlichen Verhältnissen auch nicht annähernd gerecht, behält aber immer ihre Bedeutung als Grundlage für die Betrachtung der das Phänomen bestimmenden Kräfte. Es wird bei ihr angenommen, daß jeder augenblickliche Zustand des die ganze Erde bedeckenden Meeres ein Gleichgewichtszustand sei, daß also die vorhergegangenen Zustande ohne Einfluß auf ihn seien; die Annahme würde zulässig sein, wenn die Bewegungen von Erde, Mond und Sonne unendlich langsam erfolgten. Die Anziehung des Mondes auf die Erde ist, von der Gravitationskonstanten abgesehen, gleich der Mondmasse m, dividiert durch das Quadrat der Entfernung ihrer Mittelpunkte. Hier aber kommt es nicht auf diese Gesamtanziehung, sondern auf die relative Wirkung auf die einzelnen Punkte der Erdoberfläche, verglichen mit der auf den Erdmittelpunkt, an. Man muß also die betreffenden Differenzen, natürlich im Vektorsinne, bilden; beschränkt man sich auf eine erste Annäherung, indem man den Erdradius klein gegen den Mondabstand (1 : 60) setzt, so kann man jene Differenzen durch die Differentialien ersetzen. Ferner ist es von Wichtigkeit, die resultierende Kraft in eine Vertikal- und eine Horizontalkomponente zu zerlegen, V und H. Nennt man den Winkel zwischen den vom Erdmittelpunkt nach dem Monde einerseits und dem betrachteten Erdoberflächenpunkte andererseits gezogenen Linien φ, den Erdradius a und den Mondabstand b, so erhält man die Formeln:
- V = m · (a ⁄ b3) · (3 · cos2 φ - 1),
- H = 3 · m · (a ⁄ b3) · sin φ · cos φ.
beide sind also mit der Masse des Mondes und dem Erdradius direkt, mit dem Kubus des Mondabstands umgekehrt proportional, im übrigen aber lediglich von dem Winkel φ, und zwar für jede der beiden Kräfte in verschiedener Weise abhängig; nennt man also die Linie vom Erdmittelpunkt nach dem Monde die Achse und jeden auf ihr senkrechten Kreis einen Parallelkreis, so ist die Flutkraft für alle Punkte eines Parallelkreises die gleiche, dagegen von Parallelkreis zu Parallelkreis verschieden. Und zwar ist die Horizontalkraft auf jeder Halbkugel nach deren Mondpol gerichtet und in entsprechenden Punkten gleich und entgegengesetzt; im Äquator (immer auf die Mondachse bezogen) sowie in den Polen ist sie null, in den beiden Parallelkreisen von 45° Breite ist sie am größten, nämlich gleich 3 ⁄ 2 · m · (a ⁄ b3). Die Vertikalkraft andererseits ist in den beiden Polkappen bis zu 54° 44′ 8″ nach außen, in der mittleren Zone nach innen gerichtet; in den beiden gedachten Parallelkreisen ist sie null, am größten nach außen in den Polen, nämlich 2 · m · (a ⁄ b3), am größten nach innen im Äquator, nämlich m · (a ⁄ b3), also nur halbsogroß; der Maximalwert von H ist 3 ⁄ 4. von dem von V.
Wie man sieht, findet Hochwasser nicht nur unter dem Monde statt, sondern auch für den entgegengesetzten Punkt der Erde, der den Mond im Nadir hat; man kann sich den Mond geradezu in zwei gleiche Hälften zerlegt denken und diese, diametral gegenüber aufgestellt, als Mond und Gegenmond bezeichnen. Von Laien wird die Tatsache nicht selten als paradox empfunden, indem sie meinen, im Gegenpunkte müßte tiefstes Wasser sein; es ist das eine Verwechselung absoluter und relativer Wirkung, von denen es hier nur auf die letztere ankommt; diese aber ist in beiden Polen, relativ zum Erdmittelpunkt, entgegengesetzt gerichtet, und zwar beidemal nach außen. übrigens ist die Kraft in beiden Polen nicht genau gleich groß, weil die beiden Differenzen (1 ⁄ 60)2 - (1 ⁄ 61)2 verschieden sind; sie ist vielmehr unter dem Monde um 5% größer als unter dem Gegenmonde; für jedes andere Punktpaar auf den beiden Halbkugeln besteht eine entsprechend geringere Differenz.
Berücksichtigt man jetzt die Drehung der Erde um ihre Achse, so sieht man ein, daß irgend ein Erdpunkt zweimal täglich Hochwasser und Niedrigwasser erhält, daß aber diese beiden Fluten nicht ganz gleich hoch sein werden. Man nennt das erste Phänomen die halbtägliche Flut, und das zweite, viel schwächere, die ganztägliche Flut; ihre Superposition ergibt eben die beiden verschieden hohen Fluten innerhalb eines Tages.
Berücksichtigt man weiter auch die Bewegung des Mondes, so kompliziert sich die Sache weiter. Erstens rückt jetzt die Zeit des Maximums täglich um 50 Minuten, also halbtäglich um 25 Minuten vor. Zweitens aber ändert sich die Fluthöhe mit dem Winkel, den die Mondbahn mit der Erddrehungsebene einschließt. Es kommen nunmehr vier Winkel in Betracht, nämlich die geographische Länge und Breite eines Erdortes, λ und μ, sowie der Stundenwinkel und die Deklination des Mondes, ψ und δ; um ferner, statt der Flutkraft, gleich die Fluthöhe F zu erhalten, muß man die gravitierende Kraft der Erde einführen; schließlich erhält man, wenn e die Erdmasse ist, als Quantitätsfaktor 3 ⁄ 2 · m · a4 ⁄ e · b3, und als Winkelfaktor
- F = ½ · cos2 β · cos2 δ ·(cos (2 · λ) · cos (2 · ψ) + sin (2 · λ) · sin (2 · ψ)cos (2 · λ) · cos (2 · ψ) +
- + ½ · sin (2 · β) · sin(2 · δ) · (cos λ · cos ψ + sin λ · sin ψ) +
- + 1 ⁄ 12 · (1 - 3 · cos (2 · δ)) · (3 · sin2 β - 1)
Die erste Zeile in diesem Ausdruck stellt die halbtägliche, die zweite die ganztägliche, die dritte eine neue, und zwar, wie man sieht, eine halbmonatliche oder 14tägige Flut dar; sie heißt, da sie von der Deklination des Mondes abhängt, auch die Deklinationsflut. Das Gesetz dieser Flut könnte, da es sich aus zwei Faktoren zusammensetzt, im Prinzip sehr kompliziert sein, sie könnte nämlich sowohl für gewisse δ als auch für gewisse β null werden. Indessen erreicht δ nie einen hierzu genügend großen Wert, es bleibt also nur die andere Möglichkeit übrig, und diese tritt ein für β = arcsin √(1 ⁄ 3)(1 ⁄ 3) = 35° 15′ 52″; für kleinere Breiten wird das Glied positiv, für größere negativ, solange der Mond eine mäßige Deklination hat.
Ganz die entsprechenden Betrachtungen lassen sich nun, statt für den Mond, auch für die Sonne durchführen, man erhält also eine halbtägliche, eine tägliche und eine dritte, in diesem Falle offenbar halbjährliche Sonnenflut. Die Wasserschwankungen infolge der Deklination sind aber für Sonne und Mond verschieden, da die Sonne regelmäßig zwischen 28° 27′10″ nördlich und südlich, der Mond aber je nach der Neigung seiner Bahn zwischen wechselnden Grenzen in Deklination sich bewegt. Durch das tägliche Zusammenwirken von Sonne und Mond in relativen Stellungen zueinander, die im Laufe eines Monats zwischen Konjunktur und Opposition variieren, entsteht nun das, was man die halbmonatliche Ungleichheit nennt, und was sich am extremsten eben in den Phänomenen von Springflut und Nippflut äußert. Ihr Verhältnis — nach der statischen Theorie — ergibt sich einfach aus den Massen und Entfernungen der beiden Himmelskörper mit Rücksicht auf die obige Formel für die Relativwirkung; es ergibt sich für das Verhältnis von Sonnenflut zu Mondflut 1 : 2,25 und folglich für das Verhältnis von Spring- und Nippflut etwa 2,25 + 1 : 2,25 - 1 oder 2,6 : 1. Um absolute Fluthöhen zu erhalten, muß man die irdische Schwere, die der Fluterhebung entgegenwirkt, in Betracht ziehen; man findet dann zunächst, daß die größte Verminderung der Schwere durch die Flutkraft des Mondes nur 1 / 900.0000, die größte Vermehrung sogar nur 1 / 18.000.000 ihres Wertes beträgt, und daß für die Sonne nur knapp die halben Werte gelten; und schließlich wird die ganze Niveaudifferenz zwischen Hochwasser und Niedrigwasser für den Mond 0,55 m, für die Sonne 0,24 m; die Niveaudifferenz zwischen Springflut und Springebbe würde also 0,79 m, die zwischen den Nippgezeiten 0,31 m betragen.
Zu den hier erwähnten Flutgattungen kommen nun noch zahlreiche andere, herrührend von der Veränderlichkeit der astronomischen Elemente von Erd- und Mondbahn, z. B. die wechselnden Entfernungen, die Wanderung der Knoten u.s.w.; Perioden, die teils ganzjährig, teils vieljährig, z. B. 19jährig sind, aber quantitativ zurücktreten.
Die angeführten Resultate der statischen Theorie der Gezeiten werden durch die Tatsachen in den meisten Hinsichten auch nicht annähernd bestätigt; weder ist unter dem Monde höchste Flut, noch stimmen die Nulllinien, und am schreiendsten ist der Widerspruch hinsichtlich der Fluthöhe, die für verschiedene Orte sehr verschieden ist und, statt nach Bruchteilen eines Meters zu messen, bis zu vielen Metern hinaufgeht. Es ist ohne weiteres einleuchtend, daß diese Unstimmigkeit aus zwei verschiedenen Quellen fließt: aus dem Umstand, daß die Erdoberfläche nicht gleichförmig von Wasser bedeckt ist, sondern eine sehr unregelmäßige Verteilung von Land und Wasser aufweist, und aus dem Umstand, daß es sich nicht um ein hydrostatisches, sondern um ein hydrodynamisches Problem handelt. Was den ersten Punkt betrifft, so ist es natürlich unmöglich, die Konfiguration von Wasser und Land in mathematischer Form in Betracht zu ziehen; man kann aber immerhin die wesentlichen Modifikationen feststellen, die zu erwarten sind. Es ergibt sich, daß die halbtägliche Flut nicht mehr an den Polen und die ganztägliche nicht mehr an Polen und Äquator verschwindet; endlich verschwindet die halbmonatliche bezw. halbjährliche Flut nicht mehr unter der durch β0 = arcsin √(1 ⁄ 3) charakterisierten Breite, sondern unter der durch arcsin √[(1 + ε) ⁄ 3], wo ε der Mittelwert von 3 · sin (β - 1) für den mit Wasser bedeckten Teil der nördlichen bezw. südlichen Halbkugel ist; für jene wird etwa β0 = 32, für diese 37°; das Mittel für die ganze Erde ist 34° 57′, also vom früheren nur wenig verschieden. Es muß in bezug auf das Weitere dieser Betrachtungen auf die Bücher von Thomson und Tait und Darwin und auf des letzteren Artikel in der Enc. Brit. verwiesen werden.
Dynamische Theorie. In dieser Theorie, die von Laplace begründet und nach und nach zu einem relativ hohen Grade von Vollkommenheit geführt worden ist, werden die Gezeiten als eine Art von erzwungenen Schwingungen des Wassers betrachtet, erzwungen durch äußere periodische Kräfte, nämlich durch die Anziehung von seiten des Mondes und der Sonne. Man kann die auf diesem Gedanken aufgebauten Theorien in drei Klassen einteilen, nämlich in die Kanaltheorie, die Theorie der Gezeiten ebener, d. h. relativ kleiner Gewässer und die Theorie der Gezeiten des großen Weltmeeres. Diese Theorien sind namentlich von Laplace, Green, Airy, Lord Kelvin, Lord Raleigh, Darwin, Stokes und Lamb entwickelt worden; auf die Arbeiten dieser Autoren ist hinsichtlich alles näheren zu verweisen.
Die Kanaltheorie stellt sich, um das Problem zweidimensional zu machen, einen dem Äquator parallelen, also zunächst einen äquatorialen Kanal selbst, von überall gleichem Querschnitt, geringer Tiefe und geringen Niveauschwankungen vor. Die Differenz der tangentialen Beschleunigungen von Wasser und Erde, also die relative tangentiale Beschleunigung des Wassers gegen die feste Erde infolge der Einwirkung eines Himmelskörpers ist alsdann (Bezeichnung wie oben):
- 3 ⁄ 2 · m · a ⁄ b2 · sin (2 · φ)
- φ = 2 · π · (t ⁄T - x ⁄ l)
zu setzen. Das ist also der Kraftwert X, der in die zweite der beiden Grundgleichungen erzwungener Wellen (c = √(g · h) die Fortpflanzungsgeschwindigkeit):
Die Periode ist also halbtägig, und die Flut ist direkt oder invers (d. h. unter dem Monde ist Hoch- oder Niedrigwasser), je nachdem c2 > l2 ⁄ T2 oder c2 < l2 ⁄ T2 ist, d. h. je nachdem die Welle schneller oder langsamer als der Mond um die Erde läuft. Nun ist das Weltmeer bei weitem nicht so tief, daß der erste Fall eintreten könnte; die halbtägige Flut ist also immer invers — ein Ergebnis, das also dem der statischen Theorie genau entgegengesetzt ist. — Liegt der Kanal nicht im Äquator, sondern in einem Parallelkreise, so bleiben die Fluten bis zu einer gewissen geographischen Breite des Kanals noch invers, darüber hinaus aber werden sie direkt. Ist die Fluthöhe und die Geschwindigkeit der Flutwelle nicht mehr klein, so hört die Welle auf, stationär und symmetrisch zu sein, und die Verhältnisse werden kompliziert. In noch höherem Maße ist letzteres der Fall, wenn der Kanal nicht gleichmäßige Tiefe hat, sondern nach bestimmtem Gesetz flacher wird, und wenn er vielleicht außerdem auch schmäler wird; die Flutwelle nimmt dann entsprechend an Höhe zu, aber die Einzelheiten bedürfen eingehender Untersuchung (Anwendung auf Meerengen, Flußmündungen u. s. w.). — Betrachtet man endlich einen mit einem Meridian zusammenfallenden Kanal, so erhält man, wenn der Mond im Meridian steht, mit Rücksicht auf die bei der Erde verwirklichten Zahlenverhältnisse in Breiten über 45° Flut, unter 45° Ebbe, das Umgekehrte aber, wenn der Mond um 90° vom Meridian entfernt ist.
Ebene, flache Meeresfläche. In dem zweiten der obigen Probleme hat man es mit allen drei Koordinaten zu tun; nach dem in der allgemeinen Wellentheorie Gesagten wird man demnach hier auf Besselsche Funktionen geführt und kann die Rechnung für Kreis- und Ringflächen leicht bis zu einem gewissen Grade durchführen; ebenso für rechteckige Becken. Es kommt nur darauf an, den Übergang von den früher betrachteten freien zu den hier geltenden erzwungenen Schwingungen zu machen, und es ergibt sich dabei natürlich eine besonders kräftige — ohne Rücksicht auf die Reibung sogar unendlich starke — Flut im Falle der Resonanz, d. h. wenn die Periode der erzwungenen Schwingungen mit der der freien übereinstimmt.
Weltmeer. Bei dem dritten Problem, mit dem man sich der gewünschten dynamischen Gezeitentheorie am meisten nähert, kann man, insoweit es sich um die drei Haupttypen, die halb-, ganztägige und halbmonatliche bezw. halbjährliche Flut handelt, unmittelbar an die obige statische Formel anknüpfen, muß diese aber nunmehr mit den Lösungen kombinieren, die die dynamischen Gleichungen für die Strömungsgeschwindigkeit in der Langen- und Breitenrichtung ergeben. In erster Annäherung hängt bei der halbtäglichen Flut alles von der geographischen Breite β ab, also, wenn man cos β = μ setzt, von der Größe μ; nach Potenzen von ihr kann man die dynamische Fluthöhe F′ im Vergleich zur statischen F entwickeln, wobei natürlich die Wassertiefe entscheidend mitspricht. Für drei Werte derselben, nämlich 2.206, 8.827 und 17.654 m, hat schon Laplace die Rechnung durchgeführt und z. B. für die mittlere (die etwa den größten Ozeantiefen entspricht)
- F′ = F · (μ2 + 6,1960 · μ4 + 3,2474 · μ6 + 0,7238 · μ8 + 0,0919 · μ10 + 0,0076 · μ12 + 0,0004 · μ14
- F′1 = -7,434 · F, F′2 = +11,267 · F, F′3 = +1,924 · F;
die Flut am Äquator ist also im ersten Falle invers, in den beiden anderen direkt; auch ist sie, namentlich in den beiden ersten Fällen, sehr viel stärker als die statische Flut. In mittleren Breiten findet der Wechsel von inverser zu direkter Flut bei bestimmten Meerestiefen statt, in der Nähe der Pole ist sie stets direkt. — Am merkwürdigsten wird das Resultat für die ganztägliche Flut; es ergibt sich nämlich in erster Annäherung zu null, d. h. es findet keine Spiegeländerung statt (wohl aber seitliche Strömungen); auch dieses Ergebnis verdankt man schon Laplace, der hierdurch die geringe Höhe der täglichen Gezeiten zuerst verständlich machte. — Dagegen hat sich Laplace mit der dritten Reihe, den langwelligen Fluten, nicht beschäftigt, weil er für sie die statische Theorie für ausreichend hielt. Indessen ergibt eine auch nur angenäherte Berechnung, daß das nicht der Fall ist; die dynamische Fluthöhe (für den Mond) wird nämlich z. B. für 8.827 m Meerestiefe am äquator nur 7 ⁄ 10 , und am Pole sogar nur knapp die Hälfte der statischen; für 2.206 m Meerestiefe werden die entsprechenden Zahlen gar nur knapp ½ bezw. knapp 1 / 8.
Harmonische Analyse und Synthese der Gezeiten. Aus der gegebenen Skizze der Theorie läßt sich ersehen, wie wenig Aussicht es bietet, den zeitlichen und örtlichen Verlauf der Gezeiten im einzelnen und in einigermaßen exakter Weise aus den theoretischen Formeln ableiten zu wollen. Man ist daher zu einem anderen Verfahren übergegangen, das sich mehr an die Erfahrung hält, und dieses Verfahren hat in der Tat glänzende Erfolge aufzuweisen. Man kann es als eine Art von Extrapolation von der Vergangenheit und Gegenwart in die Zukunft hinein bezeichnen; nun ist zwar im allgemeinen eine solche Extrapolation sehr gefährlich; hier aber, wo kein Grund vorliegt, anzunehmen, daß die ursächlichen Faktoren, die die Gezeiten bestimmen, sich plötzlich oder auch nur mit merklicher Geschwindigkeit allmählich ändern, da vielmehr alles mit astronomischer Genauigkeit bekannt ist, liegt irgend ein Bedenken nicht vor. Man verzeichnet also erstens die Schwankungen des Spiegels nach dem graphischen Verfahren, löst die so erhaltene Kurve in ihre Elemente vom einfach harmonischen (Sinus-) Charakter auf, was bekanntlich immer möglich ist, setzt die so erhaltenen Sinuskurven in die Zukunft hinein fort und setzt aus ihnen nun rückwärts wieder die zukünftige Flutkurve zusammen.
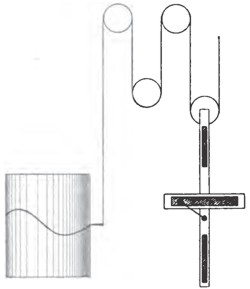
 Im einzelnen ist über dieses Verfahren kurz folgendes zu bemerken. Zur Erledigung der ersten Aufgabe dienen die Flutmesser, deren Konstruktion, trotz der offensichtlichen Schwierigkeiten, gegenwärtig eine große Vollkommenheit erlangt hat. Ein gewöhnlicher Pegel ist offenbar nicht brauchbar, weil er die Flutbewegungen von den übrigen Bewegungen des Wassers nicht sondert und weil seine Ablesung, zumal man ihn in einigem Abstand von der Küste aufstellen müßte, unbequem und ungenau sein würde. Man verwendet daher das Prinzip der kommunizierenden Röhren, läßt eine möglichst weit ins Meer hinausragende Horizontalröhre sowohl draußen als auch an der Küste in ein Vertikalrohr münden und setzt auf den Wasserspiegel in letzterem einen Schwimmer; verbindet man diesen noch mit Hilfe eines feinen Drahtes mit einem Mechanismus zur graphischen Aufzeichnung auf einer rotierenden Trommel, und gibt man dem ganzen Apparat eine so große Schwere und Trägheit, daß alle nicht zur Sache gehörigen Bewegungen wirkungslos bleiben, so hat man den W. Thomsonschen selbstregistrierenden Flutmesser, der häufig noch mit einem Integraphen zur Angabe des mittleren Wasserstandes verbunden wird und in verschiedenen Ausführungen (Newman, Stahlberger, Reitz u. s. w.) in Hafenplätzen und an Inseln aufgestellt ist.
Im einzelnen ist über dieses Verfahren kurz folgendes zu bemerken. Zur Erledigung der ersten Aufgabe dienen die Flutmesser, deren Konstruktion, trotz der offensichtlichen Schwierigkeiten, gegenwärtig eine große Vollkommenheit erlangt hat. Ein gewöhnlicher Pegel ist offenbar nicht brauchbar, weil er die Flutbewegungen von den übrigen Bewegungen des Wassers nicht sondert und weil seine Ablesung, zumal man ihn in einigem Abstand von der Küste aufstellen müßte, unbequem und ungenau sein würde. Man verwendet daher das Prinzip der kommunizierenden Röhren, läßt eine möglichst weit ins Meer hinausragende Horizontalröhre sowohl draußen als auch an der Küste in ein Vertikalrohr münden und setzt auf den Wasserspiegel in letzterem einen Schwimmer; verbindet man diesen noch mit Hilfe eines feinen Drahtes mit einem Mechanismus zur graphischen Aufzeichnung auf einer rotierenden Trommel, und gibt man dem ganzen Apparat eine so große Schwere und Trägheit, daß alle nicht zur Sache gehörigen Bewegungen wirkungslos bleiben, so hat man den W. Thomsonschen selbstregistrierenden Flutmesser, der häufig noch mit einem Integraphen zur Angabe des mittleren Wasserstandes verbunden wird und in verschiedenen Ausführungen (Newman, Stahlberger, Reitz u. s. w.) in Hafenplätzen und an Inseln aufgestellt ist.
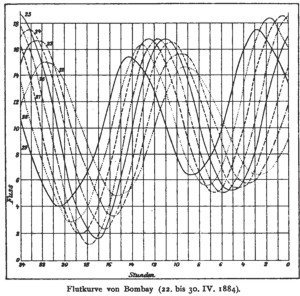
 Die Kurven, die die Instrumente liefern, sind von großer Feinheit und Gleichmäßigkeit, haben im großen und ganzen natürlich Wellenform, lassen aber im einzelnen die verschiedenen Einflüsse von Mond- und Sonnenstellung deutlich erkennen. Die Abbildung gibt eine Probe solcher Diagramme; die Papiertrommel ist achtmal hintereinander vom Stift beschrieben, die kleinen Unregelmäßigkeiten infolge von Wellenbewegung anderer Natur sind weggelassen, ein Umlauf entspricht 24 Stunden, und da die Flutperiode etwas länger ist, fallen die acht Kurven deutlich auseinander. Auch für den zweiten Teil der Aufgabe, die Reduktion der Beobachtungen, d. h. die Zerlegung der Kurven in Sinuskurven von bestimmten Perioden und Amplituden, haben J. und W. Thomson einen genialen mechanischen Apparat erfunden, den "harmonischen Analysator", dessen Spitze man nur längs der vom Flutmesser gelieferten Kurve hinzuführen braucht, um die bezüglichen Zahlenkoeffizienten zu erhalten. Diese harmonischen Analysatoren sind dann vielfach modifiziert und vervollkommnet worden, z. B. in Gestalt der Sommerfeld-Wiechertschen Integriermaschine. Hat man keine derartige Maschine, so muß man die Koeffizienten als Fouriersche Integrale von der bekannten Form darstellen und ausrechnen, was, wie man sich vorstellen wird, zu äußerst umfangreichen Rechnungen führt. Endlich hat, was den dritten Teil der Aufgabe, die Synthese für die Zukunft betrifft, ebenfalls William Thomson die Idee und Theorie eines seitdem in der Konstruktion von Roberts und Leger vielfach in Gebrauch gekommenen "Flutankündigers" gegeben, der im wesentlichen aus Systemen von Rollen, festen und beweglichen, besteht, von denen die beweglichen durch einen Kreuzschlitz derart mit Kurbeln verbunden sind, daß deren Umdrehung auf sie in Gestalt von vertikaler Auf- und Abschwingung übertragen wird; gibt man nun diesen Kurbeln die geeigneten Radien und Drehungsgeschwindigkeiten, so kann man die einzelnen Flutkomponenten durch sie wiedergeben, von Rolle zu Rolle superponieren, und der Schreibstift wird die gesamte Flutkurve beschreiben. Der Apparat in seiner Ausführung ist natürlich sehr kompliziert, das Schema wird aber durch die Abbildung genügend wiedergegeben. Je mehr Rollen der Apparat hat, desto mehr Komponenten kann er darstellen; der indische Apparat hat z. B. nicht weniger als 24 Rollen.
Die Kurven, die die Instrumente liefern, sind von großer Feinheit und Gleichmäßigkeit, haben im großen und ganzen natürlich Wellenform, lassen aber im einzelnen die verschiedenen Einflüsse von Mond- und Sonnenstellung deutlich erkennen. Die Abbildung gibt eine Probe solcher Diagramme; die Papiertrommel ist achtmal hintereinander vom Stift beschrieben, die kleinen Unregelmäßigkeiten infolge von Wellenbewegung anderer Natur sind weggelassen, ein Umlauf entspricht 24 Stunden, und da die Flutperiode etwas länger ist, fallen die acht Kurven deutlich auseinander. Auch für den zweiten Teil der Aufgabe, die Reduktion der Beobachtungen, d. h. die Zerlegung der Kurven in Sinuskurven von bestimmten Perioden und Amplituden, haben J. und W. Thomson einen genialen mechanischen Apparat erfunden, den "harmonischen Analysator", dessen Spitze man nur längs der vom Flutmesser gelieferten Kurve hinzuführen braucht, um die bezüglichen Zahlenkoeffizienten zu erhalten. Diese harmonischen Analysatoren sind dann vielfach modifiziert und vervollkommnet worden, z. B. in Gestalt der Sommerfeld-Wiechertschen Integriermaschine. Hat man keine derartige Maschine, so muß man die Koeffizienten als Fouriersche Integrale von der bekannten Form darstellen und ausrechnen, was, wie man sich vorstellen wird, zu äußerst umfangreichen Rechnungen führt. Endlich hat, was den dritten Teil der Aufgabe, die Synthese für die Zukunft betrifft, ebenfalls William Thomson die Idee und Theorie eines seitdem in der Konstruktion von Roberts und Leger vielfach in Gebrauch gekommenen "Flutankündigers" gegeben, der im wesentlichen aus Systemen von Rollen, festen und beweglichen, besteht, von denen die beweglichen durch einen Kreuzschlitz derart mit Kurbeln verbunden sind, daß deren Umdrehung auf sie in Gestalt von vertikaler Auf- und Abschwingung übertragen wird; gibt man nun diesen Kurbeln die geeigneten Radien und Drehungsgeschwindigkeiten, so kann man die einzelnen Flutkomponenten durch sie wiedergeben, von Rolle zu Rolle superponieren, und der Schreibstift wird die gesamte Flutkurve beschreiben. Der Apparat in seiner Ausführung ist natürlich sehr kompliziert, das Schema wird aber durch die Abbildung genügend wiedergegeben. Je mehr Rollen der Apparat hat, desto mehr Komponenten kann er darstellen; der indische Apparat hat z. B. nicht weniger als 24 Rollen.
Resultate. Was nun die Ergebnisse dieser, wie man sie nennen kann, empirischen Theorie betrifft, so sind sie, wenigstens wenn nicht besondere meteorologische Störungen hinzutreten und das Resultat trüben, überraschend günstig, und sie werden mit der Vervollkommnung der Analyse und Synthese von Jahr zu Jahr günstiger; natürlich verhalten sich hier auch verschiedene Breitengebiete und die einzelnen Hafenorte — denn um solche handelt es sich in der Praxis fast immer — sehr verschieden.
Die Ergebnisse können entweder in der Gestalt von Fluttafeln bezw. Gezeitentafeln oder aber, noch anschaulicher, in der Form von Flutkarten oder Gezeitenkarten dargestellt werden. In dieser Hinsicht sind England, Indien und Amerika vorangegangen; neuerdings folgt aber Deutschland nach, und die von der Seewarte herausgegebenen Vierteljahrskarten sowie der kürzlich erschienene Gezeitenatlas für die deutschen Meere gehören zum vortrefflichsten auf dem vorliegenden Gebiete.
Es gibt nur wenige Orte, für die am Tage von Voll- und Neumond das Hochwasser im Augenblick der Kulmination des Mondes eintritt, für die also die Hafenzeit null ist — freilich auch nur wenige, wo um diese Zeit Niedrigwasser herrscht; die Beharrung des Wassers und der Einfluß der Kontinente setzt sich eben in komplizierter Weise zusammen. Für irgend einen Tag findet man die Zeit des Hochwassers, wenn man zur Kulminationszeit des Mondes die Hafenzeit addiert und wegen der halbmonatlichen Ungleichheit (s. o.) folgende aus zahlreichen Beobachtungen abgeleitete Korrektion vornimmt:
| Kulmination | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | Uhr |
| Korrektur | -13 | -28 | -43 | -55 | -63 | -63 | -44 | -15 | +9 | +16 | +11 | Minuten |
Verbindet man alle Punkte mit gleichen Hafenzeiten, so erhält man die Flutwellenlinien oder Isorachien, die erkennen lassen, wie sich das Hochwasser aus den Ozeanen in die Kanäle und Binnenmeere fortpflanzt. Das Meer wird dadurch in zwei Teile geteilt, einen mit (zurzeit) Flutströmung, den anderen mit Ebbeströmung; dazwischen liegen vielfach Meeresteile, die sich im gezeitlichen Ruhezustand befinden. Im folgenden sind für einige deutsche Orte Hafenzeit und mittlerer Flutwechsel (Höhendifferenz zwischen mittlerer Flut und mittlerer Ebbe) in Metern angegeben:
| Nordsee | Elbe | Ostsee | ||||||
| Norderney | 10 h 53 m | 2,4 | Cuxhaven | 0 h 49 m | 2,8 | Fehmarn | 5 h 45 m | 0,060 |
| Helgoland | 11 h 30 m | 2,1 | Glückstadt | 2 h 52 m | 2,9 | Arcona | 8 h 35 m | 0,020 |
| Emden | 0 h 17 m | 2,8 | Hamburg | 5 h 10 m | 1,9 | Swinemünde | 11 h 30 m | 0,018 |
| Wilhelmshafen | 0 h 50 m | 3,5 | ||||||
| Bremerhafen | 1 h 4 m | 3,3 | ||||||
In der Mitte der großen Ozeane beträgt der Flutwechsel nur Bruchteile eines Meters, andererseits im Golf von Bristol bis zu 10 und in der Fundy Bai bis zu 15 m. Außerdem erhält man bei Springflut überall fast die doppelten der obigen Werte. Herrscht bei Springflut — eventuell auch bei gewöhnlicher Flut — außerdem noch ein heftiger, vom offenen Meere nach der Küste gerichteter Wind, so tritt das berüchtigte Phänomen der Sturmflut auf.
Ergänzungen. Zu der obigen Skizze der Lehre von den Gezeiten sind noch einige Zusätze zu machen, teils Nebenerscheinungen, teils Anwendungen betreffend. Die erste jener Erscheinungen ist die sogen. Flutreibung, d. h. die Wechselwirkung zwischen flutströmender Flüssigkeit und festem Erdkörper bezw., allgemeiner gesagt, Weltkörper — denn für andere Himmelskörper müssen ja ganz entsprechende Betrachtungen gelten. Soweit es sich bei dieser Wechselwirkung um einen Einfluß auf die Flüssigkeit handelt, ist sie in die obigen Theorien als Korrektion einzuführen, was indessen bei der ohnehin schon so großen Komplikation und Unzulänglichkeit dieser Theorie zunächst keine große Bedeutung hat; in der harmonischen Analyse und Synthese aber ist die Reibung ohnedies bis zu einem gewissen Grade mit enthalten. Interessant dagegen ist die andere Seite jenes Einflusses, nämlich die Rückwirkung der Gezeiten auf den festen Weltkörper. Die Flutreibung muß nämlich die Achsendrehung des Körpers so lange verlangsamen, bis sie der Umdrehung um den Zentralkörper gleich geworden ist; bei dem Monde, dem Saturnmonde Japetus und, wie es scheint, dem Planeten Merkur, ist das, ihren betreffenden Hauptkörpern gegenüber, schon jetzt der Fall. Was die Erde betrifft, so muß sich infolge der Mondfluten die Länge des Tages immer mehr steigern, bis sie der, inzwischen freilich ebenfalls gewachsenen Monatslänge gleich geworden ist; eine angenäherte Rechnung ergibt, daß alsdann Tag wie Monat eine Länge von 55 jetzigen Tagen haben werden; die Mondflut ist alsdann festgelegt. Die Sache verwickelt sich aber dadurch, daß dann immer noch veränderliche Sonnenfluten bestehen, diese werden den Tag über den Monat hinaus weiter verlängern, und infolgedessen werden von neuem Mondfluten entstehen; die so veränderten Verhältnisse werden weiter auf die Mondbahn einwirken, den Mond der Erde spiralig nähern und schließlich auf die Erde stürzen lassen.
Die zweite der gedachten Erscheinungen betrifft die Gezeiten des luftförmigen Erdmantels einerseits, was in die Aerodynamik gehört, und die Gezeiten des festen Erdkernes andererseits. Wäre die Erde vollkommen starr, so müßten sich alle Gezeiten in voller Größe offenbaren; ist sie es nicht, so muß sie. wie namentlich W. Thomson theoretisch gezeigt hat, der Wirkung besonders der langfristigeren Gezeiten in erheblichem Grade nachgeben, und wir können nur die Differenzen zwischen den Deformationen des Ozeans und des Erdkernes beobachten. Leider läßt sich diese Frage zurzeit noch nicht mit Sicherheit entscheiden; denn die gut erforschten Gezeiten von kurzer Periode können sehr wahrscheinlich auf den Erdkern, seiner großen Trägheit wegen, nicht merklich wirken, und die langfristigen sind noch nicht genügend in ihrer Amplitude bekannt. Man vergleiche hierzu die Arbeiten von W. Thomson, Darwin, Becker, Love und Chree.
Schließlich ist der Gedanke zu erwähnen, von der Gezeitenbewegung eine praktische Anwendung zu machen. Daß in der Flutbewegung des Meeres eine große Energiemenge steckt, ist einleuchtend; auch ist in dem periodischen Niveauwechsel jener Kontrast gegeben, der nach dem zweiten Hauptsatze außerdem noch zur Leistung von Arbeit erforderlich ist. Andererseits kommt die lange Periode als ungünstiges Moment in Betracht, als weiteres die Unterbrechung während des Ebbestromes. Aus diesen Gründen haben sich derartige Flutmühlen oder Flutmotoren meist nicht bewahrt; aussichtsreich und zum Teil schon in befriedigendem Gange sind sie nur dort, wo es tunlich ist, eine größere Wassermasse in einem relativ kleinen Becken oder noch besser in zwei solchen (einem Flut- und einem Ebbebecken) abzufangen und durch selbsttätige Schleusen zum offenen Meere in Beziehung zu setzen; auch ist eine Anlage erforderlich, die eine akkumulative Ausgleichung und gleichförmige Verteilung der Energie gestattet; man vergleiche z. B. den neuesten Vorschlag von Saunders im Scient. Amer. (16. IX. 1905 über die ökonomische Güte solcher Anlagen, wie sie z. B. in Kalifornien und Frankreich in Betrieb sind, lauten die Angaben noch widersprechend.
Literatur zur physikalischen Gezeitenlehre
- Isaac Newton, Philosophiae naturalis principia math., Buch I, prop. 66 (1667).
- Pierre-Simon Laplace, Mécanique célestr, L. 4 (1799).
- William Whewell, Philosophical Transactions of the Royal Society 126 (1836), pp. 289-341.
- William Thomson & Peter Guthrie Tailt, Handbuch der theoretischen Physik, § 803. (dt. Übersetz.: H. Helmhotz, G. Wertheim, Braunschweig 1874.)
- George Biddell Airy, Enc. Metrop. Lond. 1845.
- Siegmund Günther, Lehrbuch der Geophysik, Stuttgart 1884.
- George Gabriel Stokes, Cambr. a. Dubl. math. Journ. 1849.
- George Green, Note on the Motion of Waves in Canals. Cambridge Philosophical Society Transactions 1839.
- William Ferrel, United St. Coast. Surv. 1874
- George Howard Darwin, Trans. Roy. Soc. 1. I. 1879
- John William Strutt, 3rd Baron Rayleigh, Phil. Mag. (5) 1 257, 1876.
- Fridolin Becker, Sill. Journ. (3) 39, 336. 1890.
- Augustus Edward Hough Love, Cambr. phil. Trans. 16. 107. 1891.
- Jules Henri Poincaré, C. R. 118. 948.
- Charles Chree, Cambr. phil. Trans. 16. 133, 1897.
- K. Honda, Phys. Ztschr. 1905.
- Georg von Boguslawski, Otto Krümmel, Handbuch der Ozeanographie. 1887.
Quelle
Felix Auerbach: Wellenbewegung in Flüssigkeiten; in:
Handbuch der Physik, Band 1 Teil 2, Adolf Winkelmann (Herausg.), Leipzig 1908.
|
|
© Rainer Stumpe URL: www.rainerstumpe.de |