Ortsbestimmungen
Horizontalwinkel von drei Objekten
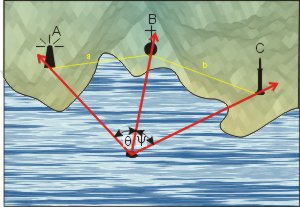Diese Ortsbestimmung mit dem Sextanten ist völlig unabhängig vom Kompass und sehr genau.
Man peilt drei Objekte A, B, C an und misst die beiden Winkel θ und ψ. Der Karte entnimmt man die Entfernungen A-B und B-C (Hier liegt eine mögliche Ungenauigkeit: die Kartendaten von See- und Landkarten stimmen nicht überein; man sollte darauf achten, dass die Landmarken als Seezeichen markiert sind! Sonst könnten sich ihre Koordinaten auf ein anderes Kartendatum beziehen.). Der Schiffsort befindet sich auf dem Schnittpunkt zweier Kreise, die jeweils die Strecken AB bzw. BC als Sehne haben. Die Kunst ist es, die Mittelpunkte M1 und M2 dieser beiden Kreis zu finden — die zugehörigen Radien r1 und r2 sind dann ja die Strecken M1A und M2C und die Strecken M1Ob und M2Ob.
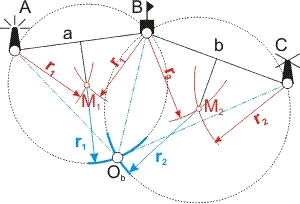
Die Lösung bietet der Sehnensatz. Nach Euklid ist der Winkel ∠AM1B doppelt so groß wie der Winkel ∠AObB. Da wir im Dreieck AM1B den gepeilten Winkel θ und die Basis AB (aus der Karte) kennen, und wissen dass AM1 = BM1 und ∠BAM1 = ∠ABM1 (gleichschenkliges Dreieck!), halbiert die Höhe hM1 die Strecke AB. Also ist nach der Definition der Winkelfunktionen
- sin α = · AM1 ⁄ ½ AB
- und da (Winkelsumme im Dreieck)
- α = β = ½ (180° - 2 · θ) = 90° - θ
- r1 = AM1 = M1Ob = ½ · AB · cos θ
- r2 = CM2 = M2Ob = ½ · BC · cos ψ.
Man kann also die Radien r1 und r2 der Kreise um die Peilobjekte A, B und C mit dem Rechenschieber einfach berechnen, um A und um B je einen Kreis mit dem Radius r1 schlagen, und um B und um C je einen Kreis mit Radius r2. Dann schlägt man einen Kreis mit dem Radius r1 um den Schnittpunkt M1 und einen Kreis mit dem Radius r2 um den Schnittpunkt M2 deren Schnittpunkt ist der gesuchte Schiffsort Ob, dessen Koordinaten man der Karte entnimmt. Diese Methode ist unabhängig von Kompassrichtungen und GPS-Daten. Sie dient also zur Ermittlung der Kompassabweichung und zur Fehlerbestimmung der GPS-Ortsangaben.
Die Kombination von Rechnung und Konstruktion geht schneller als die reine Konstruktionslösung.
