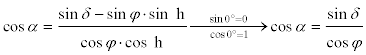Der "indische Kreis"
Zur Bestimmung der Himmelsrichtungen ist in den mittleren Breiten die Bahn der Sonne nicht geeignet. Zwar kulminiert sie überall auf der Welt genau im Süden, aber aus dem Kulminationspunkt der Sonne zu Mittag läßt sich die Südrichtung nur ungenau bestimmen — auch nicht mit einem Schattenstab (oder Gnomon).
 Zwischen 10° vor und 10° nach der Kulmination ändert sich die Höhe der Sonne nur um 1 bis 2 Grad. Es gibt aber steinzeitliche Funde [1], die auf 1° und besser auf die Himmelsrichtungen ausgerichtet sind! (Hier wurde der Sonnenhöchststand als "Mittag" bezeichnet. Das ist die Definition. Allerdings findet das nicht unbedingt
um 12:00h statt, jedenfalls nicht in einem modernen Zeitsystem, z.B. MEZ, UTC, u.ä. Die frühen Ackerbauern wird das wenig interessiert haben, den sie hatten ja keine Uhr.) Aber in den Vor- und Nachmittagsstunden entsprechen kurze Zeitintervalls großen Sonnenhöhenänderungen.
Zwischen 10° vor und 10° nach der Kulmination ändert sich die Höhe der Sonne nur um 1 bis 2 Grad. Es gibt aber steinzeitliche Funde [1], die auf 1° und besser auf die Himmelsrichtungen ausgerichtet sind! (Hier wurde der Sonnenhöchststand als "Mittag" bezeichnet. Das ist die Definition. Allerdings findet das nicht unbedingt
um 12:00h statt, jedenfalls nicht in einem modernen Zeitsystem, z.B. MEZ, UTC, u.ä. Die frühen Ackerbauern wird das wenig interessiert haben, den sie hatten ja keine Uhr.) Aber in den Vor- und Nachmittagsstunden entsprechen kurze Zeitintervalls großen Sonnenhöhenänderungen.
Die in alten Gräbern beobachetet Genauigkeit erreicht man mit einer Anordnung, die als "indischer Kreis" bezeichnet wird. Sie ist wohl recht alt, denn sie wurde bei vielen Kulturen auf allen Kontinenten beschrieben. Sie wird als "indisch" bezeichnet, weil die schriftliche Überlieferung aus Indien stammt [2]. Die Kenntnis davon kommt durch den Kriegsingenieur Caesars Marcus Vitruvius auf uns [3, 5].
Man rammt eine Stab in den Boden und zieht einen Kreis um dem Fuß des Stabes als Mittelpunkt. Der Schatten, den der Stab wirft berührt — bei richtiger Wahl der Länge des Stabes und des Durchmessers des Kreises — den Kreis am Vormittag und am Nachmittag. Die Verbindungslinie der beiden Berührungspunkte ist die Ost-West-Richtung. Um die Nord-Süd-Richtung zu finden, errichtet man das Lot im Mittelpunkt der Sehne. Dazu markiert man die Berührungspunkte des Schattens mit dem Kreis durch Pflöcke, andenen man ein Schnur befestigt, die etwa doppelt so lang ist wie der Abstand der Pflöcke und in der Mitte einen Knoten hat. Spannt man die Schnur nun einmal in die eine, einmal in die andere Richtung, findet man den nördlichen und den südlichen Punkt mit dem Knoten [4].

Nun erkennt man leicht, dass die Länge l des Schattens zu Mittag von der Höhe α der Sonne über dem Horizont abhängt — und natürlich von der Höhe h des Stabes: l = h ⁄ tan α.

Zur Länge des Stabs im Verhältnis zum Durchmesser des Kreises schreibt Vitruv [3] im 6. Kapitel des 1. Buches (S. 44 in der vorliegenden Quelle):
Collocetur ad libellam marmoreum amussium mediis moenibus, aut locus ita expoliatur ad regulam et libellam, ut amussium non desideretur; supraque eius loci centrum medium collocetur aeneus gnomon, indagator umbrae, qui . Graece σκιαδηρας dicitur. Huius antemeridianam circiter horam quintam sumenda est extrema gnomonis umbra et puncto signanda; deinde circino diducto ad punctum, quod est gnomonis umbrae longitudinis signum, ex eo a centro circumagenda linea rotundationis. Itemque observanda postmeridiana istius gnomonis crescens umbra, et cum tetigerit circinationis lineam, et fecerit parem antemeridianae umbrae postmeridianam, signanda puncto. Ex his duobus signis circino decussatim describendum, et per decussationem et medium centrum linea perducenda ad extremum, ut habeatur meridiana et septentrionalis regio.
Da die Römer den Tag von Sonnenaufgang bis Sonnenuntergang in 12 Stunden einteilten, ist die "fünfte Stunde" (hora quinta) also gegen 11 Uhr (Ortszeit!).
In Rom (12° Ost, 41° Nord) beobachtet man für einen 10 m hohen Stab (Obelisk?):
| Datum | Zeit | Azimuth | Höhe | Schatten [m] |
|---|---|---|---|---|
| 21.3. | Kulm | 180° | 49° 24′ | 8,57 |
| Kulm - 1 | 157° 13,5′ | 47° 5′ | 9,30 | |
| 21.6. | Kulm | 180° | 72° 26′ | 3,17 |
| Kulm - 1 | 138° 53,5′ | 68° 11′ | 4,00 | |
| 21.9. | Kulm | 180° | 49° 33′ | 8,53 |
| Kulm - 1 | 157° 32′ | 47° 20′ | 9,22 | |
| 21.12. | Kulm | 180° | 25° 34′ | 20,90 |
| Kulm - 1 | 164° 39′ | 24° 1′ | 22,44 | |
Man wird also die Himmelsrichtungen um den längsten Tag des Jahres herum bestimmen: dann ist der Längenunterschied des Schattens von der 5. zur 6. Stunde am größten, und gleichzeitig wandert die Sonne — und damit das Schattenende — in dieser Stunde am weitesten. Der Kreis um einen 10 m hohen Stab hat dann einen Durchmesser von etwa 8 m.
Wie sähe ein indischer Kreis bei uns aus, also etwa 10° weiter nördlich?
| Datum | Zeit | Azimuth | Höhe | Schatten [m] |
|---|---|---|---|---|
| 21.3. | Kulm | 180° | 39° 24′ | 12,17 |
| Kulm - 1 | 160° 52,5′ | 37° 48,5′ | 12,89 | |
| 21.6. | Kulm | 180° | 62° 26′ | 5,22 |
| Kulm - 1 | 151° 24′ | 60° 5,5′ | 5,75 | |
| 21.9. | Kulm | 180° | 39° 33′ | 12,11 |
| Kulm - 1 | 160° 50,5′ | 37° 59′ | 12,81 | |
| 21.12. | Kulm | 180° | 15° 33,5′ | 35,92 |
| Kulm - 1 | 165° 49′ | 14° 24′ | 38,95 | |
Die Schattenlänge ist wieder für einen 10 m hohen Stab berechnet. Der Kreis um den Fuß des Stabes hätte also einen Durchmesser von 11,5 m.
Die Formeln zur Berechnung des Sonnenstandes findet man unter den Anwendungen und den Rechenbeispielen im Kapitel "sphärische Trigonometrie".
Zur Berechnung der Richtung und Höhe der Sonne
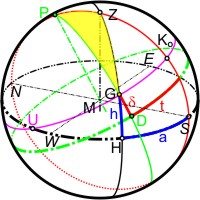 Richtung und Höhe der Sonne zu einer beliebigen Zeit berechnet man im Navigations-Dreieck, wie das bei der Berechnung der Tageslänge erklärt wird. In der Abbildung sind das Horizontsystem (der Beobachter steht im Mittelpunkt M der Kugel mit Blickrichtung nach Süden und hat den Zenith Z direkt über sich) und das Äquatorsystem (in dem sich die Sterne G auf Kleinkreisen um die Weltachse PM bewegen) überlagert. Das gelbe sphärische Dreieck ist das Navigations-Dreieck, das die beiden Koordinatensysteme verbindet. Es ist sphärisch, weil die drei Seiten PG, PZ und GZ auf Großkreisen liegen. Ihre Längen sind: PG = 90° - δ, PZ = 90° - φ und GZ = 90° - h.
Richtung und Höhe der Sonne zu einer beliebigen Zeit berechnet man im Navigations-Dreieck, wie das bei der Berechnung der Tageslänge erklärt wird. In der Abbildung sind das Horizontsystem (der Beobachter steht im Mittelpunkt M der Kugel mit Blickrichtung nach Süden und hat den Zenith Z direkt über sich) und das Äquatorsystem (in dem sich die Sterne G auf Kleinkreisen um die Weltachse PM bewegen) überlagert. Das gelbe sphärische Dreieck ist das Navigations-Dreieck, das die beiden Koordinatensysteme verbindet. Es ist sphärisch, weil die drei Seiten PG, PZ und GZ auf Großkreisen liegen. Ihre Längen sind: PG = 90° - δ, PZ = 90° - φ und GZ = 90° - h.
Für die Deklination δ und den Stundenwinkel t (auch Rektaszension α genannt) des Sterns im Äquatorsystem gibt es Tabellen, die sogenannten Ephemeriden. Damit ist die Länge des Großkreisbogens GP bekannt. Der Azimuth a ist durch die Tageszeit vorgegeben, für die man die Höhe h sucht (eigentlich: das Zeitintervall bis bzw. seit Kulmination). Sie ist ein Maß für den Winkel ∠GPS. Die Höhe h liegt auf dem Großkreis durch den Zenith Z und den aktuellen Sternort G, also ist die Seite GZ des gelben sphärischen Dreiecks zu berechnen, denn h = 90° - GZ. Die Dreieckseite PZ entspricht dem Komplement der geografischen Breite 90° - φ des Beobachtungsortes.
- bekannte Dreiecksseiten:
- PG = 90° - δ,
- PZ = 90° - φ.
- bekannter weil vorgegebener Winkel:
- ∠GPZ = β = 180° - ∠HZS = 180° - a.
- gesuchte Dreiecksseite:
- GZ = 90° - h.
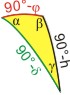 Es handelt sich damit um die V. Grundaufgabe im schiefwinkligen sphärischen Dreieck: gegeben sind zwei Seiten (GP = z und PZ = g) und ein Gegenwinkel (∠PZG = β), gesucht wird die dritte Seite GZ. Die Formel lautet:
Es handelt sich damit um die V. Grundaufgabe im schiefwinkligen sphärischen Dreieck: gegeben sind zwei Seiten (GP = z und PZ = g) und ein Gegenwinkel (∠PZG = β), gesucht wird die dritte Seite GZ. Die Formel lautet:
- tan (90° - h) = tan (90° - φ) · cos β + tan (90° - δ) · cos α = cot h = cot φ · cos β + cot δ · cos α.
(Nicht wirklich geeignet für den Rechenschieber!)
Den fehlenden Winkel α findet man mit der Argumentation, die im Zusammenhang mit der Berechnung der Tageslänge erklärt wird: α = t.
Die Deklination δ und den Stundenwinkel t findet man in Deklinationstabellen der Sonne. Dort sind für jeden Tag des Jahres der Abstand der Sternenbahn vom Himmelsäquator angegeben und der Abstand vom Frühlingspunkt ♈ zum Kulminationszeitpunkt ("Mittag"). Am 21. März finden wir
- 21. März:
- t = 0 h 1 m 26,5 s
- δ = 0° 9′ 21″
- 22. März:
- t = 0 h 5 m 5,2 s
- δ = 0° 33′ 3″
also der Stundenwinkel t um 3 m 33,5 s in 24 Stunden, uns die Deklination δ um 13′ 42″ im gleichen Zeitraum. Hier sollen sie konstant und gleich 0 angesehen werden. Als geografische Breite des Beobachters wählen wir die Nord-Süd Mitte Deutschlands: φ = 51 1⁄3° (Leipzig). Da eine Erdumdrehung 24 h dauert und 360° entspricht, ist der Winkel ∠HZS 15° pro Stunde Zeitintervall zur Kulmination. Für eine Stunde vor und nach Mittag ist β = 180° ± 15°. (Da der cos (180° ± α) = - cos α brauchen wir das Vorzeichen nicht zu berücksichtigen.)
- cot h = cot 51,3° · cos (180° - 15°) = 0,801 · 0,966 = 0,774 ⇒ h = 37,74° = 37° 44,4′
Hinweis: Das entspricht nicht der beobachtbaren Wirklichkeit. Wir haben zu viele Vereinfachungen eingeführt! Die Angaben in den Tabellen oben beruhen auf der Astronomie-Software Asynx.
Die Richtung, in der die Sonne je eine Stunde vor und nach der Kulmination steht steht, liest man direkt aus der Skizze ab: es sind 15° vor bzw. nach Mittag. Da "Mittag" die Südrichtung, also rechtweisend 180° ist, steht sie um 11 h (Ortszeit!) bei 165°, um 13 h bei 195°.
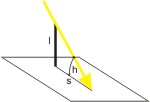 Wie lang ist nun der Schatten eines 10 m hohen Stabes am 21. März? Man erkennt das rechtwinklige Dreieck, und in dem gilt: tan h = l ⁄ s. ⇒ s = l ⁄ tan h.
Wie lang ist nun der Schatten eines 10 m hohen Stabes am 21. März? Man erkennt das rechtwinklige Dreieck, und in dem gilt: tan h = l ⁄ s. ⇒ s = l ⁄ tan h.
- Schattenlänge zu Mittag (h =38,7°): 12,5 m
- eine Stunde früher (h = 37,74°): 12,9 m
- eine Stunde später (h = 37,74°): 12,9 m
Zur Bestimmung der Kompassmissweisung
Eine interessante Anwendung der Formel
- cot h = cot φ · cos β + cot δ · cos α.
habe ich im Lehrbuch der Navigation der kaiserlichen Marine gefunden. Bei Sonnenaufgang ist h = = 0. Man erhält also
- 0 = cot φ · cos β + cot δ · cos α.
Dabei ist:
- δ = ε die Deklination bei Sonnenaufgang gleich der Schiefe der Ekliptik
- φ ist die geographische Breite
- β = 180° - α
Löst man nach cos α auf und setzt sin 0 = 0 bzw. cos 0 = 0 erhält man:
Die Richtung des Sonnenaufgangs hängt also nur von der geographischen Breite φ und der Schiefe der Ekliptik ε ab. Sie ist sehr genau zu bestimmen. Das Reichsmarineamt empfiehlt, die Richtung zu nehmen, wenn die Sonne 4 ⁄ 5 über der Kimm steht (wegen der Parallaxe und der Refraktion steht die Sonne in Wahrheit noch unter dem Horizont, wenn ihr Unterrand die Kimm berührt!).
Während man als Navigator auf See natürlich die Breite φ des Standorts kennt und die Schiefe der Ekliptik ε kennt (z. B. auch den Ephemeridentafeln am 21. März), ist das an Land wesentlich schwieriger. Nicht zu sprechen von der Bestimmung der Parallaxe und der Refraktion und dem nicht definierten Horizont.
Wenn man nun aber jungsteinzeitliche Bodendenkmäler oder Steinkreise auf ihre astronomische Ausrichtung untersuchen will, hat man das Problem der Schiefe der Ekliptik. Die kann man nämlich rückwirkend gar nicht bestimmen. Zwar gibt Wolfhard Schlosser (Lit. 1) eine schlichte Kurve auf der Basis der Präzession und der Nutation der Erdachse an. Bereits 1941 hatte Milutin Milanković die Theorie von Zyklen aufgestellt, die Überlagerung von Bahnunregelmäßigkeiten der Erde und der Schwankung der Erdachse reletiv zur Ekliptik führe zu Eiszeiten. Dies konnte Anhand der Analyse von Eisbohrkernen von J. R. Petit et al. für einen Zeitraum bis 420.000 Jahren vor unserer Zeit bestätigt werden.
Die Messungen von J. R. Petit et al. zeigen auch, dass parallel zur Temperaturerhöhung auch die atmosphärischen Konzentrationen von Kohlendioxid und Methan angestiegen sind. Und das schon vor 410.000 Jahren. Was sagt uns das über die antropogene Klimaerwärmung?
Literatur
- Wolfhard Schlosser und Jan Cierny, "Sterne und Steine — Eine praktische Astronomie der Vorzeit", 1996. Darmstadt. Wissenschaftliche Buchgesellschaft.
s. a. Schmidt-Kahler Th, Schlosser W: Stone-Age Burials as a Hint to Prehistoric Astronomy. J. Roy. Astron. Soc. Can., 78 (5), 178 - 188, 1984. - Kãtyãyana-Sulbasûtra (ca. 400 v. Chr.), Indusgebiet. (siehe englischsprachige Wikipedia für mehr Details.)
- Marcus Vitruvius Pollio (ca. 14 v. Chr.), De architectura. Druckausgabe Gotha, (1857) als PDF
- Helmuth Gericke, Mathematik in Antike und Orient, 1984. Springer-Verlag Berlin Heidelberg
- Helmuth Gericke, Mathematik im Abendland, 1990. Springer-Verlag Berlin Heidelberg
- Reichs-Marine-Amt (Herausg.): Lehrbuch der Navigation. Bd. 2, S. 152: Astronomische Navigation. 1906.
- J. R. Petit et al. Climate and atmospheric history of the past 420,000 years from the Vostok ice core, Antarctica. NATURE |VOL 399 | 3 JUNE 1999 p. 429.
- Milutin Milanković: Kanon der Erdbestrahlung . Belgrad 1941.
Kurzbiographie
- Marcus Vitrivius Pollio
- römischer Architekt, diente unter Caesar und Augustus als Pionier in der Armee und entwarf Kriegsmaschinen. Nach seiner Pensionierung faßte er die bekannte (vor allem griechische) Architektur in dem 10-bändigen Werk "De Architectura" zusammen (verm. um 15 v.Chr. entstanden). (nach: encyclopedia.com)
- Zum Thema "sphärische Trigonometrie" gehörende Seiten:
- [sphärische Trigonometrie - Grundlagen]
- [Das rechtwinklige sphärische Dreieck]
- [Das schiefwinklige sphärische Dreieck]
- [Anwendungen der sphärische Trigonometrie] (Orthodrome, Tageslänge, Deklination der Sonne)
- [Anwendungen der sphärische Trigonometrie] (Sonnenhöhe, indischer Kreis)
- [Die Nepersche Regel]
- [Beispielrechnung]
- [Konstruktion mit Projektion der Kugel]
|
© Rainer Stumpe, URL: www.rainerstumpe.de/ | |