Liber Quintus.
Theoricae Doctrinae secundus.
De Circulis Eccentrisis, Seu Theoriis Planetarum.
Pars Altera.

I. De Nominatione.

I. Über die Bezeichnungen.

Quomodo circulus denominat & discernit arcum Ellipseos, & quibus mediis, & quare?
Cum elliptica circumferentia te ipsa geometrice nequeatin partes aequales dividi, partesve constitutae, a numero denominati: circulus igitur, Ellipsis loco, dividitur in partes aequales, ab Apsidibus initio facto: & a divisionum punctis ducuntur perpendiculars in lineam Apsidum, secants Ellipsia. Arcus igitur circuli, aphelium inter & unamquamque perpendicularem, nomen dat arcui Elliptico, inter eosdem terminus intercepti, accomodans illi suum numerum graduum & minutorum.
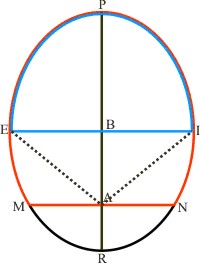
Sit PK gr 50 0 pr KL perpendicularis in PR secans Ellipsin in C. Ergo & arcem Ellipseos PC dicitur esse Graduum 50.0 pr.

Auf welche Weise bestimmt der Kreis den Ellipsenbogen und wie unterscheidet er sich, und in welcher Weise und warum?
Mit geometrischen Methoden allein kann man den Ellipsenumfang nicht in gleich groß Abschnitte teilen, aber man kann eine Teilung des Kreises in eine bestimmte Anzahl gleicher Abschnitte erzeugen: der Kreis also in gleiche Abschnitte geteilt, legt die Positionen auf der Ellipse fest: ausgehend von den Apsiden: und von den Teilungspunkten kann man Senkrechte auf die Apsidenlinie zeichnen, die die Ellipse schneiden. Der Kreisbogen daher zwischen der Apsis und einer der Senkrechten, gibt seinen Namen dem Ellipsenbogen, zwischen deren Schnittpunkt, und passt seine Grad- und Minutenzahl an.
Es sei der Bogen PK 50 gr. 0 min KL die Senkrechte auf PR, die die Ellipse in C schneidet. Also nennen wir den Ellipsenbogen PC er habe 50 gr. 0 min.

Atqui falsum est nomen, cum non sit tantus arcus Ellipseos, neque respect circuli, neque respect sua totius orbita Elliptica?
Nihil hoc turbat, nihil est enim, in praesentia quidem, nisi nomen: & nomen quidem non mensurae apparentis, sed determinationis & resectionis Geometricae: ne copus est sciri genuinam longitudine, ipsius arcus Elliptici, veluti ad mesam ad decempedam: dummodo postea sciamus, hic ipse arcus Ellipseos sic determinatus, quantum angulum faciat apud centrum Solis, & quamdiu planeta commoretur in eo. Quid? Quod prima huius libri V parte demonstro, arcum Ellipseos, si non longitudine, at saltem potestate, tantum esse.

Obwohl der Name falsch ist, denn der Ellipsebogen ist nicht so groß, und er berücksichtigt weder den Kreis, noch den ganzen Ellipsenbogen?
Das stört nicht, denn in dieser Darstellung wird nichts als der Name verwendet, und der Name ist offensichtlich nicht gemessen, für die Benennung und die geometrische Entfernung: die wahre Größe der Läge eben dieses Ellipsenbogen kennen wir nicht, gleichwie bei der Messung an der Meßlatte, werden wir sie erst im Nachhinein, an dieser Stelle wird der Ellipsenbogen so bestimmt, welcher Winkel mit der Sonne eingeschlossen wird, und solange der Planet an dem Ort verweilt. Wie? Weshalb ich im ersten Teil dieses Buches V gezeigt habe, der Ellipsenbogen ist so groß, nicht seine Länge ist so groß, wie der Abstand [von der Apsis].

Quomodo perpendiculars ista, sectrices Ellipseos appelantur?
In circulo, dicuntur sinus arcuum circuli, inceptoru ab Aphelio: in Ellipsi, generis voce dicutur ordinatim applicatae, puta ad axem. Ut hic KL est sinus arcus KP. CL est ordinatim applicate.
In specie vero, illa quae per centrum figurae ducitur, ut EBI diameter brevior, seu figurae latus rectum dicitur. Possumus uti Graeca voce Diacentros. Quae denique; per centrum solis traiicitur ut MAN nomine caret, licet sit inter praecipuas. Dicatur novo vocabulo Dihelios.

Wie werden diese Senkrechten genannt, die die Ellipse schneiden?
Im Kreis, wird der Sinus des Kreisbogens benutzt, der ausgehend vom Aphelium gezählt wird: in der Ellipse wird statt dessen die Ordinate verwendet, nämlich entlang der Achse. Wie hier KL der Sinus des Bogens KP ist, ist CL die benutzte Ordinate.
Die wahre Länge haben jene, die wir durch das Zentrum der Figur ziehen, wie EBI die kürzere Achse ist, oder wenn die Figur die rechten Länge zeigt. Wir können den griechischen Begriff "Diazentrum" [Mittelpunktstrahl]gebrauchen. Solche schließlich, die durch das Zentrum der Sonne gezogen werden, wie MAN, sei es erlaubt, ebenfalls einen zu geben. Wir verwenden ein neues Wort: Dihelios [Brennpunktstrahl].

Anm. d. Übers.: Kepler überträgt hier die Definition der Arcusfunktion "Sinus" analog auf die Ellipse.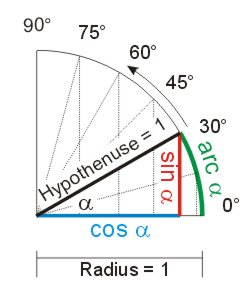

So wie der Einheitskreisbogen ein Maß für den Sinus des Winkels zwischen der x-Achse und dem Strahl (im Bild Hypothenuse) ist, definiert er einen "Sonnenstrahl" der in der Ellipse den Winkel einschließt, dessen Maß der Abschnitt auf dem Lot, das die Ellipse schneidet, ist.

Quodnam est officium illarum perpendicularium, Diacentri & Dihelii?
Dividunt orbitam in partes, superiorem & inferiorem, illa quidem in aequales, sed temporis & apparentiae inaequalis: haec in partes quidem inaequales & tempore & longitudine, sed quae tamen, velut ex sole apparent aequales.
Ut EPI qua constituitur ab EBI est quidem 180 Graduum, sed apparet angulo EAI minore, quam 180 Graduum. At MPN segmentum maius absectum linea MAN & MRN segementum minus, utrumque apparet aquale quantitate 180 Graduum.

Was ist dann der Nutzen jener Senkrechten zum Mittelpunktstrahl und zum Brennpunktstrahl?
Sie teilen den Kreis in Abschnitte, einen oberen und einen unteren, jene wiederum in gleiche Teile, aber mit ungleichen Zeitabschnitten: auf dieser Seite gerade ungleiche Teile von Zeit und Länge, aber welche dennoch von der Sonne aus gleich erscheinen.
So wie EPI, das von EBI gebildet wird, und 180 Grad entspricht, aber der Winkel EAI erscheint kleiner als 180 Grad. Dagegen werden durch die Linie MAN das große Segment MPN und das kleine Segment MRN abgeschnitten, beiden Segmente erscheinen gleich groß mit 180 Grad [von Brennpunkt A aus gesehen].