Die Keplersche Gleichung
Die große Leistung Johannes Keplers war es, die Gesetze über die Bewegung der Planeten aus den Beobachtungen ihrer Bewegungen zu erkennen und zu formulieren. Dabei stieß er auf die Probleme, die Länge eines Ellipsenabschnitts zwischen zwei beliebigen Punkten und die Fläche eines Ellipsensektors in der Brennpunktsform berechnen zu müssen. Das zweite Problem konnte er lösen, zum ersten erkannte er, dass das mit Infinitesimalrechnung möglich wäre — aber die kannte er nicht (sie wurde erst von Issac Newton für diese Frage entwickelt).
Die Fläche eines Ellipsensegments war notwendig, um das 2. Gesetz zu beweisen ("Die Fahrstrahlen der Planeten überstreichen in gleichen Zeiträumen die gleichen Flächen."). Heute kann man das durch Integrieren der entsprechenden Differenzialgleichung, aber zu Keplers Zeit, war die Differenzialrechnung eben noch nicht erfunden. Da er an der Berechnung des Planetenortes auf seiner elliptischen Bahn interessiert war, musste er die Länge des Ellipsenbogens vom sonnenfernsten Punkt kennen. Für diese Bestimmung benutzte Kepler die klassische Geometrie und erhielt die Kepler-Gleichung: M = E - ε·sin E.
Seine Formulierung, die Kepler-Gleichung, wird zwar viel zitiert, aber nur bruchstückhaft erklärt. Die von ihm vergebenen Bezeichnungen, werden noch heute benutzt. Hier soll die Herleitung verständlich dargestellt werden.
Hinweise für den geneigten & kritischen Leser:
- Die hier dargestellten Überlegungen Keplers basieren ausschließlich auf euklidischer Geometrie. Die physikalische Begründung der Planetenbahnen hat erst Isaac Newton mit dem Postulat der Schwerkraft geliefert.
- Ja, Wikipedia (und andere Quellen) definieren die "mittlere Anomalie" anders. Aber nur mit der hier dargestellten Definition kann man die Kepler-Gleichung schlüssig ableiten.
- Bitte lesen Sie meine Übersetzung zusammen mit dem Originaltext von Johannes Kepler in meinen Erläuterungen zur mittleren Anomalie bei Johannes Kepler
- Die hier dargestellte Ableitung der Kepler-Gleichung fand ich in wesentlichen Teilen 10 Jahre nach meiner Erstveröffentlichung auf dieser Seite bestätigt durch die Lektüre von Keplers Werken: Astronomia Nova von 1609 und Epitomes Astronomiae Copernicanae von 1635.
- Die in anderen Quellen angegebene Ableitung basiert wohl auf Carl Friedrich Gauss "Theoria Motus Corporum Coelestium", von der es eine deutsche Übesetzung von Carl Haase (1865) gibt.
- Anmerkung für besondere Naseweise, die ein Beispiel gefunden haben, in dem die Kepler-Gleichung nicht gilt.
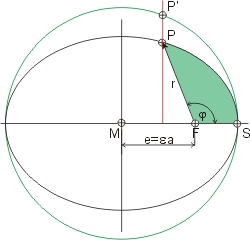 |
Grundlage der Ableitung der Kepler-Gleichung ist die Affinität der Ellipse zum Kreis. Im Kreis kann man die Flächen der Segmente leicht berechnen. Er zeichnete also einen Umkreis der Ellipse mit dem Radius der großen Halbachse a (hier grün), um die Fläche des grün gefärbten Ellipsensegments zu berechnen. Dieses ist nicht so einfach, und er mußte tief in die trigonometrische Trickkiste greifen. Dazu half ihm, dass ein Punkt P auf der Ellipse und ein Punkt P' auf dem Umkreis, die beide auf einer Sehne parallel zur kleinen Halbachse b, liegen, die gleiche x- und ein bekanntes y-Koordinatenverhältnis haben b/a. Es gilt also: xP = xP' und yP = b/a·yP'. |
Nun ist die Fläche des Kreissegments FFSP' nicht direkt auszurechnen, aber die eines Kreissegments FMSP' ist berechenbar.
 |
Das Kreissegment MSP' hat die Fläche FMSP' = π·a2·E/(2·π), also den Bruchteil der Umkreisfläche, den der Winkel <P'MS an 360° = 2·π hat. Den Winkel E nannte Kepler exzentrische Anomalie". Nun kann man - wegen der Affinität - auch die Fläche FMSP des Ellipsensegments MSP angeben: man ersetzt einfach im der Kreisflächenformel r2 durch a·b, also: FMSP = π·a·b·E/(2·π) = a·b·E/2 Die Fläche FFSP des gesuchten grüne Ellipsensegment FSP erhält man, wenn man die Fläche FΔ des roten Dreiecks MFP von der Fläche FMSP des Ellipsensegments MSP abzieht. Diese Dreiecksfläche ist ja die Hälfte des Produkts aus Basis und Höhe. Die Höhe in dem Dreieck ist aber die y-Komponente von P, also: FΔ = ½·e·yP. |
Nun brauchen wir die Höhe des Dreiecks, oder die y-Koordinate von P, yP. Die ist aber, wegen der
Affinität, yP = b/a·yP'. Und yP' können wir mit dem Winkel E und dem
Radius a des Umkreises berechnen:
yP =
(b/a)·a·sin E = b·sin E.
Die Fläche des roten Dreiecks MFP ist also FΔ = ½·e·(b/a)·a·sin E = ½·e·b·sin E.
Damit ist die Fläche des Ellipsensegments FSP also:
FFSP = a·b·E/2 - ½·e·b·sin E = (b/2)·(a·E - e·sinE)
Leider hilft das nicht viel, denn die Fläche ist nun eine Funktion der exzentrischen Anomalie E, also eines Winkels am Mittelpunkt der Ellipse. Wir wollen aber eine Funktion eines Winkels am Brennpunkt. Weiter hilft eine Überlegung am Umkreis.
|
Die blaue Kreissegmentfläche FFSP' können wir - wegen der Affinität von Kreis und Ellipse - angeben: FFSP' = (a/b)·FFSP = (a/b)·(b/2)·(a·E - e·sinE)= Wenn sich der Punkt P' auf dem Kreis immer so bewegt wie der Punkt P auf der Ellipse, so wird sich die Kreissegmentfläche mit dem Winkel am Brennpunkt (<P'FS, Kepler nannte ihn die mittlere Anomalie M) verändern. Ein voller Umlauf von 360° = 2·π wird also die Kreisfläche π·a2 überstrichen haben, und in einem Bruchteil M/2π des vollen Umlaufs die Fläche FSFP' = π·a2·(M/2π) = (M/2)·a2. (Hinweis: Selbstverständlich entsprechen gleichen Änderungen des Winkels M am Brennpunkt unterschiedlich große Kreissegmente, deren Fläche vom Winkel M abhängt. Das ist der Grund für die Unlösbarkeit der Kepler Gleichung! Aber es ergibt sich das 2. Keplersche Gesetz daraus.) |
 |
Beide Formeln für die Kreissegmentfläche kann man gleichsetzen:
FFSP' = (a/2)·(a·E - e·sinE) = (M/2)·a2
In dieser Gleichung kann man a/2 kürzen und sie nach M auflösen:
M = E - (e/a)·sin E
Das ist die Keplersche Gleichung. Für e/a kann man noch ε setzen ( Definition der numerischen Exzentrizität!), dann hat man die üblicherweise zitierte Form der Gleichung. Sie wird als ästhetisch, weil einfach, empfunden.
Nun mag sie zwar schön sein, aber sie hat einen gravierenden Mangel: man kann sie nicht nach E auflösen.
Wenn man nun wissen möchte, an welcher Stelle auf der elliptischen Umlaufbahn ein Planet zu einer gegebenen Zeit steht — und Kepler wollte das —, muss man eine Hilfskonstruktion anwenden. Die mittlere Anomalie, also der Winkel am Brennpunkt, dessen Fahrstrahl den Umkreis im Punkt P' schneidet, nimmt jeden Wert zwischen 0° und 360° an, aber man kann nicht sagen, zu welcher Zeit. Andererseits entspricht jeder Punkt auf dem Umkreis aber einer Zeitspanne vom Periheldurchgang. Man rechnet also den Winkel für alle Zeiten zwischen zwei Periheldurchgängen aus nach der Formel M'(t) = (t - t0)/T·360°. (Hinweis: M'(t) ist nicht die mittlere Anomalie M, obwohl sie die gleichen Werte annimmt!). Die mittlere Anomalie M(E) rechnet man in einer zweiten Tabelle für alle Werte der exzentrischen Anomalie E aus. Dann schaut man, welche Werte von M'(t) mit welchen Werten von M(E) mit denen von M(t) übereinstimmen, und findet die zum entsprechenden Wert von E gehörende Zeit t.
Um den Planetenort berechnen zu können, benötigen wir noch ein paar Formeln. In karthesischen Koordinaten mit dem Brennpunkt F als Ursprung brauchen wir xP und yP, in Polarkoordinaten mit dem Brennpunkt F als Ursprung zu beschreiben, benötigen wir die wahre Anomalie φ und die Länge des Fahrstrahls r mit der exzentrischen Anomalie E in Beziehung setzen (die bekommen wir aus der Kepler-Gleichung für jeden Bruchteil der Umlaufzeit).
 |
Mittelpunktssystem Im gelben Dreieck MP''P' liegt ja der mit der Kepler-Gleichung berechnete Winkel E. Es hat die Katheten xP' und yP' und die Hypotenuse a (große Halbachse der Ellipse). Die Katheten xP und yP kann man berechnen. Da - im Mittelpunktssystem - xP + xP' = e = a·ε, ist xP = a·ε - xP'. Und xP' ist offensichtlich xP' = a·cos E, also lautet die Formel im Mittelpunktssystem xP = e - a·cos E = a·ε - a·cos E = a·(ε - cos E). Ebenfalls im Mittelpunktssystem wird der Winkel φ aus dem blauen Dreieck berechnet. Der Sinus seines Ergänzungswinkels φ' = (180° - φ) ist sin φ' = yP / r = sin φ (weil der Sinus der zyklisch ist). |
Für die y-Koordinate des Planeten, yP, haben wir ja weiter oben schon einen Ausruck gefunden: yP = b·sin E. Die beiden Gleichungen setzen wir gleich und lösen nach sin φ auf: sin φ = (b/r)· sin E.
Die Länge des Fahrstrahls r ist dann - nach Pythagoras (c2 = a2 + b2) - r2 = xP2 + yP2 = (e - a·cos E)2 + (b·sin E)2. Mit ein bißchen Arithmetik (man sollte sich erinnern, dass sin2 α + cos2 α = 1 und e2 = a2 - b2!), erhalten wir: r = a - e·cos E.
Diesen Ausdruck für r setzen wir in die Formel für sin φ ein:
![]()
Jetzt haben wir einen Ausdruck für die wahre Anomalie φ aus dem Mittelpunktssytsem abgeleitet, die außer der exzentrischen Anomalie E nur noch systemunabhängige Größen enthält.
Brennpunktssystem
Im Brennpunktsystem verwenden wir Polarkoordinaten, also φ und r. Da sich der Planet P auf einer Ellipsenbahn bewegt, berechnen wir r mit der polaren Brennpunktsgleichung der Ellipse aus der wahren Anomalie φ:

Erst durch die Anwendung dieser Gleichung haben wir die Änderung des Winkels φ mit einer kontinuierlichen Zeit in einer Ellipse so festgelegt, dass φ ein Winkel am Brennpunkt ist, die von der positiven x-Richtung (nach rechts) aus zählt!
Wie sieht nun das Ergebnis aus? Nehmen wir einen hypothetischen Planeten, der auf einer elliptischen Bahn mit den Halbachsen a = 100 und b = 75 Längeneinheiten seine Sonne in 200 Zeiteinheiten umkreist (es ist unerheblich, in welchen Einheiten wir Zeit und Länge messen), und plotten wir seine Position in Intervallen von 5 Zeiteinheiten.

Rein qualitativ gibt das Bild aber schon das richtige Verhalten wieder. Im Perihel sind die Abstände der Punkte gering, dafür liegen lange Ellipsenbögen zwischen den Punkten. Auf der gegenüberliegenden Seite - im Aphel - sind Radien groß und die Winkeländerungen klein. Die Berechnung wird separat erläutert.
|
|
© Rainer Stumpe URL: http://www.rainerstumpe.de |