Die Keplersche Gleichung
Die große Leistung Johannes Keplers war es, die Gesetze über die Bewegung der Planeten aus den Beobachtungen ihrer Bewegungen zu erkennen und zu formulieren. Dabei stieß er auf das Problem, die Länge eines Ellipsenabschnitts zwischen zwei beliebigen Punkten in der Brennpunktsform der Ellipse berechnen zu müssen. Da er durch die Berechnung des Planetenortes beweisen wollte, dass Planeten sich auf elliptischen Bahnen bewegen, in deren Brennpunkt die Sonne steht, musste er die Länge des Ellipsenbogens vom sonnenfernsten Punkt, dem Aphel, kennen. Für diese Bestimmung benutzte Kepler die klassische Geometrie und erhielt die Kepler-Gleichung: M = E ± ε·sin E.
Seine Formulierung, die Kepler-Gleichung, wird zwar viel zitiert, aber nur bruchstückhaft erklärt. Die von ihm vergebenen Bezeichnungen, werden noch heute benutzt. Hier soll die Herleitung verständlich dargestellt werden.
Kepler musste zur Berechnung der Planetenorte zu einer beliebigen Zeit des Umlaufes auf der elliptischen Bahn sowohl den Winkel φ, den die Verbindungslinie des Planeten zur Sonne in B vom Aphel S (sonnenfernster Punkt der Umlaufbahn) zum gegenwärtigen Punkt P einschließt, als auch die Entfernung r (Strecke BP) des Planeten zur Sonne bestimmen.
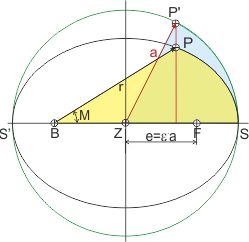 Dazu bediente er sich der Affinität der Ellipse zum Kreis. Im Kreis kann man die Flächen der Segmente leicht berechnen. Und es gibt die Beziehungen von Elementen der Ellipse zu denen des Kreises aus den Sätzen des Apollonius von Perga.
Dazu bediente er sich der Affinität der Ellipse zum Kreis. Im Kreis kann man die Flächen der Segmente leicht berechnen. Und es gibt die Beziehungen von Elementen der Ellipse zu denen des Kreises aus den Sätzen des Apollonius von Perga.
Er zeichnete also einen Umkreis der Ellipse mit dem Radius der großen Halbachse a (hier grün), um die Fläche des gelb gefärbten Ellipsensegments zu berechnen.
Apollonius von Perga (262 bis 190 v. Chr.) hatte die Erkenntnisse seiner Zeit über die Kegelschnitte in sieben Büchern zusammengefasst, von denen nur lateinische Übersetzungen "De Conicis" erhalten sind. Deren Kenntnis gehörte zum Bildungscanon eines Wissenschaftlers.
Keplers verwendet u. a. folgende Sätzen des Apollonius von Perga.
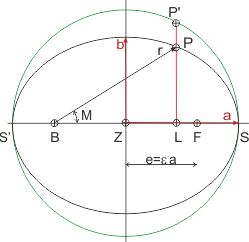 Umschreibt man eine Ellipse mit der großen Achse 2 · a und der kleinen 2 · b, mit dem Umkreis des Radius a, der die Ellipse in den beiden Scheiteln S und S' berührt, und zieht die Verbindungslinie (Apsidenlinie) zwischen den Scheiteln der Ellipse, sodass der gemeinsame Mittelpunkt Z und die Brennpunkte B und F der Ellipse auf der Apsidenlinie liegen, so gilt:
Umschreibt man eine Ellipse mit der großen Achse 2 · a und der kleinen 2 · b, mit dem Umkreis des Radius a, der die Ellipse in den beiden Scheiteln S und S' berührt, und zieht die Verbindungslinie (Apsidenlinie) zwischen den Scheiteln der Ellipse, sodass der gemeinsame Mittelpunkt Z und die Brennpunkte B und F der Ellipse auf der Apsidenlinie liegen, so gilt:
- Jede Sehne in einem Punkt L auf der Apsidenlinie, die auf der Apsidenlinie senkrecht steht, schneidet die Ellipse und den Kreis in der Weise, dass sich die Sehnenabschnitte der Ellipse zu denen des Kreises verhalten wie b zu a.
- Die Flächen von Ellipse und Umkreis verhalten sich wie b zu a.
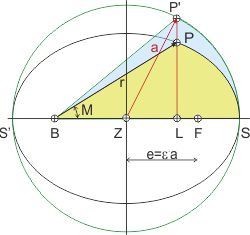
- Zieht man Verbindungslinien von Punkten, die auf einem Lot und auf den Umfängen von Kreis und Ellipse liegen, zum Brennpunkt B, so verhalten sich die Flächen der Segmente wie die Abschnitte auf dem Lot.
- Teilt man den Kreisumfang durch solche Lote in beliebig viele gleiche Abschnitte, so wird die Ellipse durch die Schnittpunkte des Lots mit dem Ellipsenumfang in ungleiche Teile geteilt. Der Unterschied der Länge der Kreisabschnitte zu denen der Ellipsenabschnitte ist am Scheitel am größten, an der kleinen Achse am kleinsten.
- Der Ellipsenumfang ist sehr nahe am arithmetischen Mittel aus Umkreis- und Inkreisumfang.
Mit der Regel Ziff 3 kann man die Fläche des gelben Ellipsensegments BPS berechnen, wenn man das blaue Kreissegment kennt.
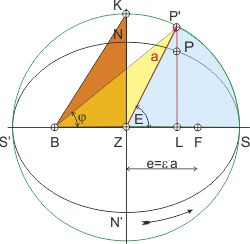 Wenn der Umkreis der Ellipse den Radius a = 1 hat (Einheitskreis), dann ist der Flächenanteil eines Kreissegments SP'Z (hier blau) an der Kreisfläche gleich dem Längenanteil des Kreisbogens SP' am Kreisumfang: FSP'Z = E ⁄ 2·π (E ist die exzentrische Anomalie).
Wenn der Umkreis der Ellipse den Radius a = 1 hat (Einheitskreis), dann ist der Flächenanteil eines Kreissegments SP'Z (hier blau) an der Kreisfläche gleich dem Längenanteil des Kreisbogens SP' am Kreisumfang: FSP'Z = E ⁄ 2·π (E ist die exzentrische Anomalie).
In dem roten Dreieck BZK sind die beiden Katheten bekannt: BZ = e, die Exzentizität, und KZ = a, die große Halbachse oder der Radius des Umkreises.
Die Fläche des gelben Dreiecks BZP' (FBZP' = ½·e·P'L) kann beim Umlauf des Punktes P' um den Kreis maximal die Größe des Dreiecks BZK (hier rot) annehmen: FBZK = ½·e·a.
Die Höhe P'L = h des gelben Dreiecks BZP' ist aber h = sin E, also ist seine Fläche FBZP' = ½·e·sin E.
Kepler stellt nun folgende Überlegung an: die Fläche des roten Dreiecks BZK ist ja ein Bruchteil der Umkreisfläche F = π·a². Die Fläche des gelben Dreiecks BZP' ist dann der Bruchteil des roten Dreiecks an der Kreisfläche multipliziert mit dem Bruchteil, um den das gelbe Dreieck kleiner ist als das rote. Da im Einheitskreis (a = 1) die Fläche als Maß für den Winkel am Brennpunkt B verstanden werden kann, läßt sich der Winkel M berechnen.
Der Anteil f des roten Dreiecks BZK an der gesamten Kreisfläche ist: f = (½·e·a) ⁄ (π·a²) = ½π · e ⁄ a. Und die Fläche des gelben Dreiecks BZP' ist FBZP' = 1 ⁄ 2π · e ⁄ a · sin E. Die Flächensumme des blauen und des gelben Dreiecks ergibt den Anteil der Fläche des Kreissektors P'BS an der Kreisfläche, und ist das Maß für den Winkel M, der nach Kepler die mittlere Anomalie ist: 1 ⁄ 2π · M = 1 ⁄ 2π · E + 1 ⁄ 2π · e ⁄ a · sin E = 1 ⁄ 2π · (E + e ⁄ a · sin E).
(Im Umkreisquadranten S'KZ nimmt man die Differenz.)
Nun kann man noch e ⁄ a durch die numerische Exzentrizität ε ersetzen: 1 ⁄ 2π · M = 1 ⁄ 2π · (E + ε· sin E), und beide Seiten der Gleichung durch ½π teilen:
M = E + ε· sin E.
Diese Kepler-Gleichung setzt die exzentrische Anomalie E, das ist der Winkel zwischen der großen Achse und der Verbindungslinie am Mittelpunkt zu einem Punkt auf der Ellipse mit der mittleren Anomalie M, das ist der Winkel am Brennpunkt zwischen der großen Achse und der Verbindungslinie zu dem Punkt auf der Ellipse in Beziehung. Neben den Variablen E und M kommen nur die für jede Ellipse spezifische Konstante, die numerische Exzentrizität ε vor. Allerdings taucht die exzentrische Anomalie E auf beiden Seiten der Gleichung auf: M - E = ε· sin E, auf der rechten als Argument einer transzendenten Winkelfunktion. Damit wird die Kepler-Gleichung eine transzendete Gleichung, d. h. man kann sie nicht lösen. Zur Zuordnung der Werte von E und M muß man die Werte der mittleren Anomalie M für einen Bereich der exzentrischen Anomalie E ausrechnen und die Wertepaare suchen, die gleich sind.
Nach 5. der obigen Regeln über die Ellipse und ihren Umkreis kann man den Umfang des Umkreises in regelmäßige Bogenstücke teilen, z. B. in 360 Teile. Jeder Teil einspricht dann einem 360tel der Umlaufzeit, oder einer Änderung des Winkels E um 1°. Der Winkel der exzentrischen Anomalie E kann also als Maß für die Zeit genommen werden, die ein Planet auf seiner Umlaufbahn vom Aphel zum gegenwärtigen Ort gebraucht hat.
Die mittlere Anomalie M dagegen ist über den Sehnenabschnitt mit der wahren Anomalie φ verknüpft; beide sind Winkel am Brennpunkt. Wenn man also die zu einer exzentrischen Anomalie E gehörende mittlere Anomalie M kennt, kann man den Winkel φ zu beliebigen Zeiten des Umlaufs berechnen.
Um den Planetenort angeben zu können, berechnen wir die karthesischen Koordinaten (Nullpunkt bei Z) des Punkts P', xP' und yP'. Daraus können wir dann die wahre Anomalie φ und die Länge r des Fahrstrahls (Abstand von der Sonne) des Punktes P berechnen.
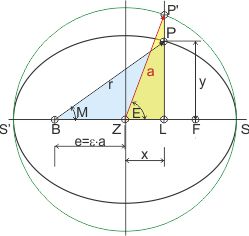 Im rechtwinkligen gelben Dreieck ZLP' sind bekannt die exzentrischen Anomalie E, und die Länge der Hypotenuse a (große Halbachse der Ellipse). Also ist xP' = a · cos E, und yP' = a · sin E. Die Strecke BL, das ist der Abstand des Fusses des Sehnenlots L vom Brennpunkt B, hat die Länge:
Im rechtwinkligen gelben Dreieck ZLP' sind bekannt die exzentrischen Anomalie E, und die Länge der Hypotenuse a (große Halbachse der Ellipse). Also ist xP' = a · cos E, und yP' = a · sin E. Die Strecke BL, das ist der Abstand des Fusses des Sehnenlots L vom Brennpunkt B, hat die Länge:
BL = e + xP' = e + a · cos E. (Wenn E ein spitzer Winkel ist.)
Die Strecke BL ist aber eine der Katheten im blauen Dreieck BLP. Die andere Kathete, LP, aber ist aus yP' zu bestimmen, denn sie ist eine Ellipsensehne und es gilt: LP ⁄ LP'= b ⁄ a. Somit ist LP = yP = b ⁄ a · a · sin E.
Nun ist die Hypotenuse r im blauen Dreieck mit dem Satz des Pytagoras zu berechnen:
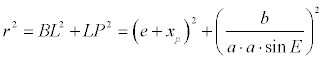
Mit ein wenig Arithmetik (man sollte sich erinnern, dass sin2 α + cos2 α = 1 und
e2 = a2 - b2), erhalten wir:
r = a + e·cos E.
Den Winkel φ — die wahre Anomalie — im blauen Dreieck berechnet man aus der Definition des Sinus:
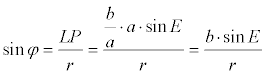
Für r substituieren wir den bereits gefundenen Ausdruck r = a + e·cos E und erhalten:
![]()
Jetzt haben wir einen Ausdruck für die wahre Anomalie φ aus dem Mittelpunktssytsem abgeleitet, die außer der exzentrischen Anomalie E nur noch konstante Größen enthält, nämlich die Längen a und b beiden Halbachsen der Ellipse.
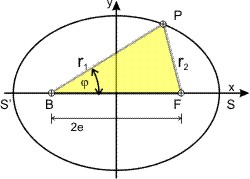 Nun brauchen wir nur noch die polare Brennpunktgleichung für den Ellipsenort herzuleiten, die die Länge des Fahrstahls r und die wahre Anomalie φ in Beziehung setzt. Dazu benutzen wir die Definition der Ellipse als geometrischen Ort aller Punkte, deren Abstandssumme von den beiden Brennpunkten B und F konstante ist: r1 + r2 = 2 · a.
Nun brauchen wir nur noch die polare Brennpunktgleichung für den Ellipsenort herzuleiten, die die Länge des Fahrstahls r und die wahre Anomalie φ in Beziehung setzt. Dazu benutzen wir die Definition der Ellipse als geometrischen Ort aller Punkte, deren Abstandssumme von den beiden Brennpunkten B und F konstante ist: r1 + r2 = 2 · a.
Da das gelbe Dreieck BPF schiefwinklich ist, gilt der Cosinussatz und wir erhalten:
r2² = r1² + (2·e)² - 4·r1·e·cos φ
Da — nach den Definitionen — r1 = 2·a - r2, e2 = a2 - b2 und ε = e ⁄ a ist, erhalten wir nach
Einsetzen und Auflösen:
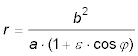
Substituiert man noch b2 ⁄ a = p erhält man die Form die C. F. Gauss angibt:
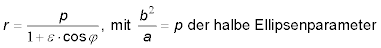
Erst durch die Anwendung dieser Gleichung haben wir die Änderung des Winkels φ am Brennpunkt mit einer kontinuierlichablaufenden Zeit auf dem Umkreis verknüpft. Diese Gleichung kannte Kepler natürlich noch nicht; ich vermute, sie stammt von Gauss — jedenfalls steht sie in seiner Theoria Motus Corporum Coelestium von 1809. Dort wird die mittlere Anomalie offensichtlich missverständlich bezeichnet.
Wie sieht nun das Ergebnis aus? Nehmen wir einen hypothetischen Planeten, der auf einer elliptischen Bahn mit den Halbachsen a = 100 und b = 75 Längeneinheiten seine Sonne in 200 Zeiteinheiten umkreist (es ist unerheblich, in welchen Einheiten wir Zeit und Länge messen), und plotten wir seine Position in Intervallen von 5 Zeiteinheiten.

Rein qualitativ gibt das Bild aber schon das richtige Verhalten wieder. Im Perihel sind die Abstände der Punkte gering, dafür liegen lange Ellipsenbögen zwischen den Punkten. Auf der gegenüberliegenden Seite - im Aphel - sind Radien groß und die Winkeländerungen klein. Die Berechnung wird separat erläutert.
![]()
Quellen:
- Johannes Kepler Astronomia Nova von 1609.(PDF)
dto., deutsche Übersetzung von Max Caspar (München 1929), herausgegeben von Fritz Krafft, Matrix Verlag Wiesbaden, 2005, ISBN 3-86539-014-5 - Johannes Kepler Epitomes Astronomiae Copernicanae, gedruckt 1635 von Johann Godefrid Schönwetter in Frankfurt. (PDF)
dto., deutsche Übersetzung von Eberhard Knobloch, Otto Schöberger und Eva Schöberger, Verlag Königshausen & Neumann Würzburg, 2010, ISBN 978-3-8260-4202-7 - Apollonii Pergaei Conicorum Libri Quatuor. Typographia Stephani Gatti, 1696. (PDF)
- Des Apollonius von Perga sieben Bücher über Kegelschnitte, Deutsch bearbeitet von B. Balsam, Verlag von Georg Reimer, Berlin, 1861. (PDF)
- Carl Friedrich Gauss, Theoria Motus Corporum Coelestium in Sectionibus Conicis Solem Ambientum, Frid. Perthes und I. H. Besser, Hamburg 1809. (PDF)
- Carl Friedrich Gauss, Theorie der Bewegung der Himmelskörper welche in Kegelschnitten die Sonne umlaufen. Deutsch von Carl Haase, Carl Meyer Hamburg, 1895. (PDF)