Der Inkreis des Dreiecks

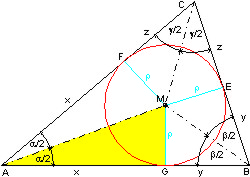Zur Konstruktion eines Kreises, der in einem Dreieck ABC liegt und alle drei Seiten berührt, sucht man den Schnittpunkt Linien, die die drei Winkel α, β und γ halbieren. Das ist der Mittelpunkt M des Inkreises. Der Radius ρ des Inkreises ist dann der Abstand des Mittelpunktes M von den Berührungspunkten des Kreises mit den Dreieckseiten.
Da die Radien ρ auf den Dreiecksseiten senkrecht stehen, entstehen 6 paarweise kongruente rechtwinklige Dreiecke, z. B. das gelb gefärbte ΔAGM. Es hat mit dem ΔAMF die Hypotenuse AM gemeinsam und den gleichen Winkel bei A (α ⁄ 2) und die eine Kathete ρ ist gleichlang. Damit sind auch die beiden anderen Katheten x gleichlang.

Die gleiche Argumentation gilt auch für die beiden anderen kongruenten Dreieckspaare. Der Umfang der Dreiecks ergibt sich also zu: U = a + b + c = 2·x + 2·y + 2·z , oder ½ · (a + b + c) = x + y + z. Für ½ · (a + b + c) setzt man zur Vereinfachung des Ausdrucks s. Und da x + y = c (c = AB), y + z = a, x + z = b, erhält man x = s - a, y = s - b, z = s - c.

Gleichzeitig gilt im gelben rechtwinkligen Dreieck AGM: tan ½·α = ρ ⁄ x = ρ ⁄ (s - a). (Definition der Tangensfunktion Gegenkathete ⁄ Ankathete.)

Und im ganzen Dreieck ABC gilt der Halbwinkelsatz:

Setzte man die beiden Formeln gleich, erhält man einen Ausdruck für den Radius ρ des dem Dreieck eingeschriebenen Kreises:
.

Diese Formel ist der Schlüssel zur Berechnung des schiefwinkligen Dreiecks, wenn nur die Längen der drei Seiten bekannt sind.

Definitionen

Kongruenz (von Dreiecken)

Zwei Dreiecke sind deckungsgleich (kongruent), wenn sie:

1. in den Längen der drei Seiten übereinstimmen,
2. in den Lägen zweier Seiten und der Größe des eingeschlossenen Winkels übereinstimmen,
3. in den Lägen zweier Seiten und der Größe des der längsten Seite gegeüberliegenden Winkel übereinstimmen,
4. in den Lägen einer Seite und den Größen der beiden anliegenden Winkel übereinstimmen.