II. De Libratione.

Doce metiri & computare librationes, & determinare intervalla?

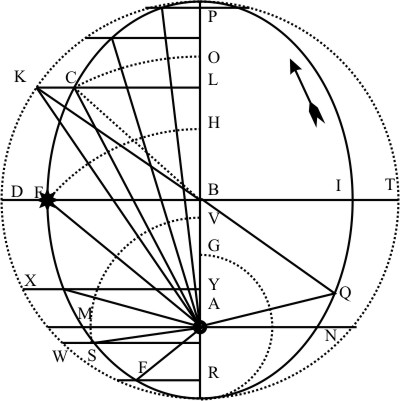
Sit PK arcus Eccentrici minor quadrante verbi causa Gr. 46 18 pr 51 sec euius ergo complementum KD erit Gr. 43.41 pr. 9 sec euiusque sinus BL 69070 & sit Eccentricitas AB; seu dimidia libratio PH 9265 qualium BP est 100000. Multiplicatur igitur 69070 in 9265 & absectis 5 ultimis prodit libratio OH 6399 addenda ad BP vel AH in superiori semicirculo EPI eritque AO vel ei aequalia AC distantia scilicet planeta a Sole 106399, competens arcui PK vel PC qualium quidem semidiameter est 100000.

Si arcus Eccentri fuerit Gr 313 41 pr 9 sec excessus super tres Quadrantes seu 270 Gr erit etiam Gr 43 41 pr 9 sec dans sinum eundem multiplicandum: quo cum extruitur libratio 6399, itidem addenda, ut addenda quippe in superiori semicirculo, sed ascendenti.

Quodsi semidiameter BP acceperit aliam dimensionem, verbi causa 152342, multiplicabimas et hanc in AC 106399 absectis 5 ultimia, et prodibit AC in hac dimensione 162090.

Artificio Neperiano conficitur tota haec operatio expeditissime per unicam additionem. Nam sinus arcus KD logarithmus additur logarithmus Eccentricitatu 9265 & Dimensionis proposita 152343 summa quasita ut Logarithmus, exhibit librationem 9748 addendam ad Dimensionem 152342.

Sic deinde arcus PW maior quadrante, scilicet Graduum 133 39 pr 7 sec Excessus super quadratem DW Gr 43 39 pr 7 sec euiusque vel sinus vel logarithmus cum dictum duobus pricipiis, prodit librationem 9777 subtrahenda ab 152341 quippe in inferiori Diacentri semicirculo, ut prodeat intervallum respondens AS 142565.

Idem erit, si arcus Eccentrici habuerit gr 226 20 pr 53 sec. Nam complementum eius ad tres quadrantes erit Grad 43 30 pr 7 sec tantus in ascendenti quantus DW in descendenti semicirculo.

Erkläre die Messung und Berechnung der Libration und die Bestimmung der Abstände?

Es sei PK der Exzentrizitätsbogen im kleineren Quadranten angenommen zu 46° 18’ 51". Und sein Komplement sei 43° 41’ 9" und dessen Sinus BL 69070 und die Exzentrizität ist AB oder deren Hälfte die Libration PH 9265, BP ist 100.000. Wird nun 69070 mit 9265 multipliziert und die letzten 5 Stellen gestrichen, bleibt die Libration OH 6399, addiert zu BP oder AH im oberen Halbkreis EPI und sei AO oder seine gleiche AC die Entfernung des Planeten von der Sonne ist selbstverständlich 106.399, und entspricht dem Bogen PK oder PC dessen Halbmesser gerade 100.000 ist.

Wenn der Bogen der Exzentrizität 313° 41’ 9" sein sollte, der Überschuss über die drei Quadranten oder 270° ist noch 43° 41’ 9" und wird mit einer Multiplikation zu dessen Sinus gegeben: wodurch mit der Libration 6399, zu jenem addiert, ausgedrückt wird wie der gleiche Addition ja im oberen Halbkreis oder Aszensenten.

Weshalb der Halbmesser BP zu der anderen Größe hinzutritt, in Worten 152.342, multiplizieren wir dies mit AC 106.399 und streichen die letzten 5 Ziffern, ergibt sich AC in der Größe 162.090. Die künstlichen Zahlen (Logarithmen) des Neper lassen diese Berechnung am schnellsten in einer einzigen Addition zu. Denn der Logarithmus des Bogens KD addiert zum Logarithmus der Exzentrizität 9265 ergibt 152.343.

So hierauf der Winkel PW in großen Quadranten, hat selbstverständlich 133° 39’ 7" Der Überschuss über den Quadranten DW ist 43° 39’ 7" so ergibt sowohl der Sinus als auch der Logarithmus mit den genannten Grundlagen eine Libration von 9.777, was abgezogen von 152.341 freilich im unteren diazentrischen Halbkreis, den zugehörigen Abstand AS 142.565 ergibt.

Gleiches gilt, wenn der exzentrische Bogen 226° 20’ 53" habe. Denn des Komplement über drei Quadranten ist 43° 30’ 7" so groß ist die Größe von DW im absteigenden Halbkreis.

Recense praecipuos librationis casus?

1. Quando planeta incipit discedere ab Apside: tunc simul libratio incipit, planeta scilicet incipit descendere versus solem: qui discessum a sole Paulo prius finiverat.
2. Quando planeta habet gradus 60 ab Apside; tunc libratio aequat semissem Excentricitatis.
3. Quando planeta quadrantem orbitae confecit ab Apsid: tunc librationis dimidium est peractum, sic ut planeta distet a sole, semidiametro Eccentrici. Ut si PD est 90 tunc AE aquat BD.
4. Quando planeta confecit gradus 120 ab Apside: tres quadrantes librationis sunt peracti.
5. Quando planeta est in ima Apside: tunc proximus soli factus, totam librationem absoluit. Contrarium est ordo per semissem Ascendentem.
6. Binae quaeque distantiae a sole, planeta aequalibus Eccentri arcubus, ille ab Aphelio, hic a Perihelio remote, junctae aequant Diametrum. Ut si ex C ducatur recta par B in Q, CA et AQ iunctae aquant RP.

Zähle besonderen Gründe der Libration auf?

1. Wenn der Planet anfängt seinen Lauf von der Apside zu nehmen: alsdann beginnt gleichzeitig die Libration, beginnt gleichzeitig den Abstieg zur Sonne hin: sie wird begrenzt von der Sonne am unteren Ende.
2. Wenn der Planet 60° von der Apside hat, alsdann gleicht die Libration der halben Exzentrizität.
3. Wenn der Planet auf dem Umlauf von der Apside den Quadranten vollendet hat: alsdann ist die halbe Libration vollendet, und der Planet ist einen exzentrischen Halbmesser von der Sonne entfernt. Und wenn PD 90° beträgt ist AE gleich BD.
4. Wenn der Planet 120° von der Apside gewandert ist, sind drei Quadranten der Libration vollendet.
5. Wenn der Planet in der unteren Apside ist: alsdann ist er der Sonne am nächsten und hat seine Libration vollendet. Für die aufsteigende Hälfte gilt die umgekehrte Reihenfolge.
6. Beide Entfernungen zur Sonne, der gleiche exzentrische Bogen des Planeten, der eine vom Aphel, der andere vom Perihel ausgehend, sind durch den gleichen Durchmesser verbunden. Und wenn man eine Gerade von C durch B nach Q zieht, sind CA und AQ zusammen gleich RP.

Erläuterung der Berechnung der Libration

Den Begriff "libratio" möchte ich hier als "Pendeln" (zwischen der oberen und der unteren Apside) verstehen. Gleichzeitig verwendet Kepler den Ausdruck offensichtlich für die Projektion des Bahnbogens auf die Apsidenlinie (grße Achse der Ellipse).

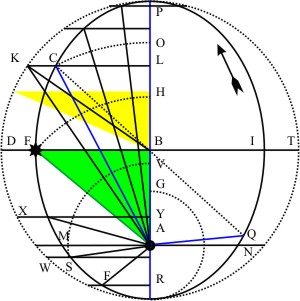Im zweiten Abschnitt dieses Kapitels gibt Kepler ein paar Hinweise zur Geometrie der Ellipse und den Strecken­ver­hält­nissen:

1. die Entfernung des Planeten zur Sonne gleich der großen Halbachse, wenn der Planet auf der kleinen Halbachse steht (grünes Dreieck),
2. zieht man eine Verbindungslinie vom Planeten durch den Mittelpunkt der Ellipse zum gegenüberliegenden Schnittpunkt, dann ist die Summe der der Abstände beider Punkte zur Sonne gleich der groß Achse der Ellipse (blaue Linien),
3. hat der Planet 60° von der Apside zurückgelegt, ist die Länge des Abschnitts vom Mittelpunkt auf der großen Halbachse gleich der halben Exzentizität (gelbes Dreieck).

[siehe auch:Ellipsengeometrie, Mittelpunktsgleichung, Brennpunktsgleichung]

Im grünen Dreieck ist die längere Kathete gleich der kleinen Halbachse b der Ellipse, die kürzere gleich der Exzentizität e. Es gilt: . Für den Abstand r des Planeten zur Sonne wenden wir den Pythagoras an: r² = b² + e² mit e² = a² - b² ⇒ r² = b² + a² - b² = a² ⇒ r = a.