Das Buch hat 74 Seiten und ist gegliedert in die Abschnitte:

• Vorwort des Autors
• Erstellung der Tabelle der wunderbaren Logarithmen?
• Anhang über eine andere Art diese Logarithmen zu erstellen
• Andere Methode die Logarithmen zu erzeugen
• Weiter Ausführungen des gelehrtesten Dr. Henry Briggs
• Vorschläge, diese auf sphärische Dreiecke anzuwenden
• Weitere Anmerkungen des gelehrtesten Dr. Henry Briggs

Mirifici Logarithmorum Canonis Constructio?
(Qui et Tabula Artificialis ab Authore deinceps appelatur)
eorumque ad naturales ipsorum numeros habitudiens.

Positio Prima.

Tabula Artificialis, est minima Tabula, cuius Logarithm opera facillimo computo omnium Geometericarum dimensionum, motuumque sublimium habetur notitia.

Hæc merio minima dictur, quia Tabulam sinuum volumine non exsuperat: facillima, quia per eam omnes multiplicationes, divisiones, extractionesque radicum graviores evitantur: solis enim & perpaucis facillimisque additionibus. subtractionibus, & bipartionibus omnes generalter figuras motusque metitur.

Hac a numeris proportione continua progredientibus excerpitur.

Pos. 2. Continuarum progressionum, alis Arithmetica que per equalia intervalla progreditur: e Alia Geometrica, qua per inequalia & proportionaliter crescentia, aut deficientia incedis.

Arithmetica progressio, ut 1, 2, 3, 3, 5, 6, 7, &c. vel 2, 4, 6, 8, 10, 12, 14, 16, &c. Geometrica vero, ut 1, 2, 4, 8, 16, 32, 64, &c. vel 243, 81, 27, 9, 3, 1.

In progressionibus requiritur accuration, & operis facilitas. Accuratio sit, pro fundamento numeros maiores accipiendo: maseres autem numeri ex minoribus facillime fiunt adiectis cyphris.

Ut pro 100000, quem rudiores sinum maximum faciunt, eruditiores ponunt 10000000, quo melius omnium sinuum discrimen exprimatur. Unde & eodem nos pro sinu toto & maximo proportionalium Geometricorum utimur.

4. In Tabulis computandis etiam ex numeris maioribus maximi fiant, interposita periodo inter numerum ipso & cypheræ adiectas.
   Ut ex 10000000, nos initio computationis facimus 10000000.0000000, ne minutissimus error frequenti multiplicatione in immensum cresceret.
5. In numeris periodo sic in se distinctis quicquid post periodum notaiur fractio est, cuius denominator est vustas cum tot cyphris post se, quot sunt figura post periodum.
   Ut 10000000.04, valet idem, quod 10000000 4 ⁄ 100. Item 25.803. idem quod 25 303 ⁄ 1000. Item 9999998.0005021, idem valet quod 9999998 5021 ⁄ 10000000. & sic de cæteris.
6. E tabulis iam computatis, reiici possunt fractiones post periodum locata, absque ullo sensibili errore. In magnis enim nostris numeris error insensibilis & quasi nullus habetur, qui unitaiem non exsupras.
   Ut completa Tabula pro 9987643.8213051, qui sunt 9987643 8213051 ⁄ 10000000, accipi possunt ya 9987643 absque sensibili errore.
7. Est praterea alia accurationis formula: quum scilicet quantitas ignora, seu numero inexplicabilis, inter erminos numerules pluribus unitabtibus non differentes includitut.
   Ut posita Diametro circuli partium 497, quia nescitur præcise quot partium sit ambitus, ideo eruditiores ex Alchimedis sententia, eum inter terminos 1562, & 1561 incluserunt. Item si costarum quadrati qualibet sit partium 1000, erit diagonalis radix quadrata numeri 1000000, que cum sit numero inexplicabilis, ideo per extractionem radicis quadratæ quæruntur eius termini, scilicet 1415 terminus maior, & 1414 terminus minor, vel 1414 604 ⁄ 2828 maior, & 1414 604 ⁄ 2829 minor videlicer quanto minor terminorum differentia sit, tanto maior accuratio.
8. Vice ipsarum quantitatum ignoratum, termini earum sunt addendi, substrahendi, multiplicandi, aut dividendi preunt opus fuerit.
9. Adduntur bini alicuius quantitatis termini ad binos terminos alterius, quum minor illius huius, & maior illius in maiorem heius ducitur.
   Ut sit linea abc, in duas quantitates ab & bc divisa; sit ab inter terminos 123.5 maiorem, & 123.2 minorem: sitque bc inter terminos 43.2 maiorem, & 43.1 minorem. Additis ergo maiore ad maiorem, & minore ad minorem. Additis ergo maiore ad maiorem, & minore ad minorem, fiet tota quantitas ac inter terminos 166.7 & 166.3.
   Multiplicantur bini alicuius quantitatis termini per binos terminos alterius, quum minor illius in minorem huius, & maior illius in maiorem haius ducitur.
   
   Ut sit altera quantitas ab, quæ sit inter terminos 10.501 maiorem, & 10.500 minorem; altera vero ac, quæ sit inter terminos 3.216 maiorem, & 3.215 minorem. Unde ductis 10.502 in 3.216, & 10.500 in 3.215, provenient termini 33.774432, & 33.757500; inter quos erit area abcd.
10. Terminorum subfiraclio fit, terminum maiorem minoris quantitatis a minore maioris, & minorum minoris a maiore maiores auferendo.
    Ut in schemate primo, so es terminis ac, qui sunt 166.7 & 166.3, subduceris terminos bc, qui sunt 43.2 & 43.1, fient 123.6 & 123.1 pro terminis ab; & non 123.5 & 123.2. Nam licet etiam horum additio ad 43.2 & 43.1, producebat 166.7 & 166.3, (per octauam) non tameu e converso sequetur, quin aliquid possit esse inter 166.7 & 166.3, ex quo si substaxeris aliquid quod sit inter 43.2 &43.2, remenæret id quod non sit inter 123.5 123.2: verum non esse id inter terminos 123.6 & 123.1 est impossibile.
11. Divisio sit, pertiendo terminum maiorem dividendi per minorem divisoris, & minorem dividendi per maiorem divisoris.
    Ut in præcedente figura, quadratum abcd inter terminos 33.774432 & 33.757500 constitutum diviatur per terminos ac, qui sunt 3.216 & 3.215, provenient 10.505. 875 ⁄ 3215 & 10.496 2364 ⁄ 3216 pro teminis ab; & non 10.502 & 10.500, eadem ratione, quam in substactione diximus.
12. Rudes terminorum fractiones delenda sunt addita unitate ad terminum maiorem.
    Ut pro terminis ab præcedentibus, scilicet 10.505. 857 ⁄ 3215 & 10.494 2364 ⁄ 3210, capiantur 10.506 & 10.496.
    hactenus accuratione, sequitur de facilitate operis.
13. Omnis pregressionis Arithmetica facilis est constructio, Geometrica autem non omnis.
    Patet hoc, siquidem additione & substractione fir facillime Arithmetica progressio: geometrica vero, difficillimis multiplicationibus, divisionibus, & radicu extractionibus continuatur.
    Sola Geometrica ille progressiones facile continuantur, que per substractionem facilis partis numeri a numero toto oriuntur.
14. Partes numeri facilis dicimus, partes quaslibet cuius denominationes unitata & cyphris quotcunque notantur: habentur aurem ha partes, reiiciendo tot figuras ultimas principalis numeri, quot sunt cyphre in denominattore.
    Ut partes decima, centesima, millesima, 10000^m, 100000^m, 1000000^m, 10000000^m, facilis dicuntur, quia cuiuslibet numeri decima pars habetur delendo eius ultimam figuram; centesima duas untlimas, millesima tres ultimas figuras, & sic de cæteris, semper delendo to figuras ultimas quot sunt cyphræ in denominatione partis. Ut decima pars huius 99321 est 9332, eius autem centesima est 993, millesima 99, &c.
15. Mediocruer etiam facile habentur partes dimidia, vigesima, ducandecentesima, & alia per binarum & cyphras denominate, reiiciendo tot figuras ultimas principalis numeri, quot sunt cyphra in denominatore, & reliquum bipartiendo.
    Ut numeri 9973218045 pars 2000^m est 4986609, pars 20000^m est 498660.
16. Hinc sequitur, si a sinu toto septem cyphris aucto, caterisque inde otti suam 10000000^am partem subtraxeris, continuari possunt quam facillime centum numeri, in eo minorem unitate, scilicet 10000000 & 9999999; hancque seriem proportionalium primam Tabulam nominamus.
    

    Prima Tabula.
    10000000.0000000
    1.0000000
    9999999.0000000
    9999999
    9999998.0000001
    9999998
    9999997.0000003
    9999997
    9999996.0000006
    continuando usque ad
    9999900.0004950

    Ut sinu toto aucto septem cyphris (maioris accurationis gratia) sic 10000000.0000000 aufer 10000000, fient 9999999.0000000: ex quibus aufer 9999999 fient 9999998.0000001; ↦ sic prosequaris ut latere, donec centum creaueris proportionalia, quorum untimum (si recte computaueris) erit 9999900.0004950.
17. Tabula secunda progreditur a sinu toto sex cyphris aucto, per quinquaginta numeros alios deficientes proportionaliter, ea proportione qua facillima est, & quam proxima proportioni, qua est ter primum & ultimum prima Tabula.
    

    Secunda Tablula.
    10000000.0000000
    100.000000
    9999900.000000
    99.999000
    9999800.001000
    99.998000
    9999700.003000
    99.997000
    9999600.006000
    &c. ut usque ad
    9995001.222927

    Ut primæ Tabulæ primum & vitimum sunt 10000000.0000000, & 9999900.0004950; in quorum proportione, difficile est constiti ere quinquaginta proportionales numeros. Proxima itaque facilis proportio, est 100000 ad 99999, quæ continuatur satis exacte adiiciendo sinui toti sex cyphras, & auferendo ab antecedente suam partem 10000^am, ut fiat subsequents, ut a latere vides: & hæc Tabula præter primum qui est sinus totus, etiam quinquaginta contineat proportionales numeros, quorum ultimum (ni erraveris) reperies esse 995001.222927.
18. tertia Tabula sexaginta nevem columnis constat, & in qualibet columna ponuntur numeri viginti & unus, progredeienses ea proportione qua facillima est, & quam proxima illi proportioni quæ est inter primum & ultimum secunda Tabula.
    Unde huius prima columna facillime habetur a sinu toto quinque cyphris aucto, & ceteris maioris suam 2000^am partem auferendo.
    

    Prima Columna tertia Tabula.
    10000000.00000
    5000.0000
    9995000.00000
    4997.5000
    9990002.50000
    4995.00125
    9985007.49875
    4992.50374
    9980014.99501
    &c. ut usque ad
    9900473.57808

    
    Ut quia inter 10000000.000000 primum secunda tabulæ, & 9995001.222927 eiundem ultimum, proportio difficilis est progressionis; ideo in proportione facili 10000 ad 9995 (quæ illi propinqua satis est) constituendi sunt numeri viginti & unus; quorum ultimus (ni ertaueris) erit 9900473.57808 A quibus iam creatis, retici potest umltima singulorum figura absque sensibili errore, quo facilibus ab iis alii postea creentur.
19. Primi numeri omnium columnarum, progreditur a sinu toto quaruor cyphris austo, ea proportione facillima & proxima proportione, qua est inter primum & ultimum prima columna.
    Ut primæ columnæ primus & ultimus sunt 10000000.0000, & 9900473.5780: his proportio facillima maxime propinqua est 100 ad 99. A sinu igitur toto continuandi sunt 68 numeri in ratione 100 ad 99, aufrerendo a quolibet eorum suam centesimam partem.
20. Eadem proportione, a prima columna numero secundo, per omnium columnarum secundos: & a tertio, per tertios: & a quarto, per quartos: & ceteris respectine, per cateros fit progressio.
    Ut ex antecedentis columnæ numero aliquo sit numerus eiundem ordinis in sequenti columna, subtrahendo suam centesimam pertem, numerosque hoc qui sequitur ordine constituendo.
    

    Proportionalia Tertiæ Tabulæ
    Prima Columna.	Secunda Col.
    10000000.0000	9900000.0000
    9995000.0000	9865050.0000
    9990002.5000	9890102.4750
    9985007.4987	9885157.4237
    9980014.9950	9880214.8451
    &c. usq; ad	&c. descendendo ad
    9900473.5780	9801468.8423
    Tertia Col.	Inde 4a.5a &c. usq. ad 69am column.
    9801000.0000	&c. usque ad	5048858.8900
    9796099.5000	&c. usque ad	5046334.4605
    9791201.4503	&c. usque ad	5043811.2932
    9786305.8495	&c. usque ad	5041289.3879
    9781412.6967	&c. usque ad	5038768.7435
    &c. descendendo ad	usque tadem ad
    9703454.1539	usque tandem ad	4998609.4034

21. In tertia ergo Tabula, habes inter sinum totum, & medium sinui totius, interiectos sexaginta octo numeros in proportione ut 100 ad 99; & rursus inter singulos binoa horum, interiectes vinginti numeros in proportione ut 10000 ad 9995: & rursus inter binos primos horum, scilicet inter 10000000 & 9995000, habes in secunda Tabula interiectos 50 numeros, in propotione ut 100000 ad 99999: & tandeminter primos horum, habes in prima Tabula interiectos centum numeros, in proportione ut 10000000 sinus totus ad 9999999; quorum differentia quum sit tantum unitatis, non est opus eam (interiectis mediis) minutius prtiri. Unde ha tres tabula (postquam completa fuerint) ad tabulam † artificialem computandum sufficient. († Logarithm.)
    Hucusque sinus seu numeros naturales proportione geometrica progredientes tabulis facillime inserere docuismus.
22. Superest Tabula saltem tertia, apud sinus sine numeros naturales geometrice decrescentes, suos † numeros artificiales Arithmesice crescentes inserere:
23. Arithmetice crescere, est equalibus temporibus equalis semper quantitate augeri.
    
    Ut ex puncto b fixo versus d, infinite producatur linea: in qua ex b versus d procedat punctus a, movens ea lege, ut æqualibus temporis momentis æqualibus feratur spatiis: quæ sint b 1, 1 2, 2 3, 3 4, 4 5, &c. Dico hoc incrementum per b 1, b 2, b 3, b 4, b 5, &c. Arithmeticum dici. In numeris autem sint b 1, 10: b 2, 20: b 3, 30: b 4, 40: b 5, 50. Dico 10, 20, 30, 40, 50, &c. Arithmetice crescere: quia æqualibus momentis, æquali numero denatii semper augeri intelliguntur.
24. Geometrice decrescere, est equalibus temporibus quantitatem primo totam, inde aliam atque alsam eius partem superstitem, simili semper proportionali parte diminui.
    
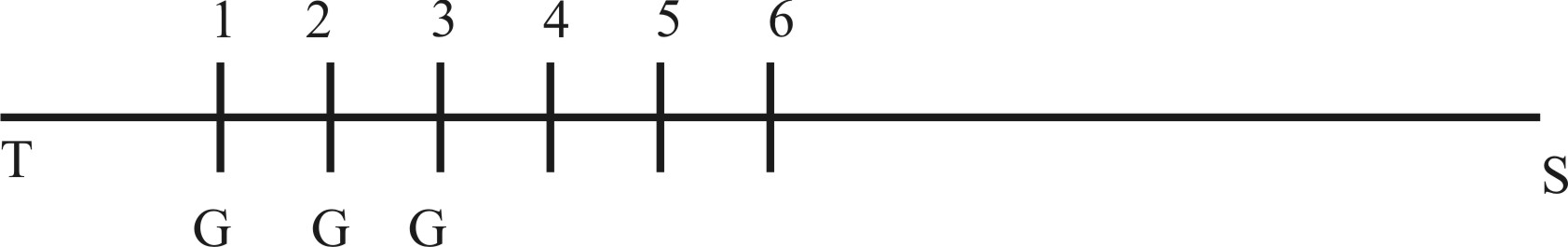
    Ut sit linea sinustitius TS, in hac moveatur punctus G, a T in 1 versus S. Quantoque tempore defertur a T in 1, quæ sit (exempli gratia) decima pars TS tanto idem G tempore moveatur ab 1 in 2, quæ sit decima pars: S & a 2 in 3, quæ sit decima pars 2 S: & a 3 in 4, quæ sit decima pars 3 S, & sic de ceteris. Dico hos sinus TS.1 S, 2 S, 3 S, 4 S, & c. dici Geometrice decrescere: quia inæqualibus spatiis proportione similibus & tempore æqualibus diminuuntur. In numeris sit TS, 10000000: 1 S, 9000000: 2 S, 8100000: 3 S, 7290000: 4 S, sit 6561000, &c. Dico hos sinuum numerus, æqualibus temporibus simili proportione diminu os, dici Geometrice decresdere.
25. Unde punctus mobilis Geometrice ad fixum accedens, velocitates suas prons distantias, a fixo proportionatas habet.
    Ut repetito præcedenti Schemate, dico quum mobilis punctus geometricus G est in T, eius velocitas est ut distantia TS: & quum G est in 1, eius velocitas est ut 1 S: & quum in 2, eius velocitas est ut 2 S, & sic de cæteris. Atque ita quæ est proportio distantiarum TS, 1 S, 2 S, 3 S, 4 S, &c. ad invicem, ea etiam erit proportio velocitatum G in punctis T, 1, 2, 3, 4, &c. adinvicem. Nam magis minusve velox punctus aguitur, prous magis minusve longe sub æqualibus temporibus ferri conspicitur. Qualis itaque processus ratio, talem etiam & velocitatum esse necesse est: at talis est sub æqualibus temporibus ratio processuum T 1, 1 2, 2 3, 3 4, 4 5, &c. qualis distantiarum TS, 1S, 2S, 3S, 4S, &c. ut mox docebimus. Unde necessario qualis habitudo distantiarum G ab S, videlitatum G in punctus T, 1, 2, 3, 4, &c. quod erat demonstrandum. At quod processuum T 1, 1 2, 2 3, 3 4, 4 5, &c. talis sit ratio, qualis distantiarum TS, 1S, 2S, 3S, 4S, &c. patet: quia quantitatum proportionaliter continuatatum differentiæ etiam in eadem proportione continuantur. At hæ distantiæ (per hypothesim) proportionaliter continuantur, & illi processus sunt harum differentiæ: quare eadem processus qua distantias ratione continuati certum est.
26. † Numerus artificialis sinus, dati est qui Arithmetice crevit tanta semper velocitate, quanta sinus totus inceptis Geometrice decrescere, tantoque sempere, quanto sinus totus in sinum illum datum decrenis.
    
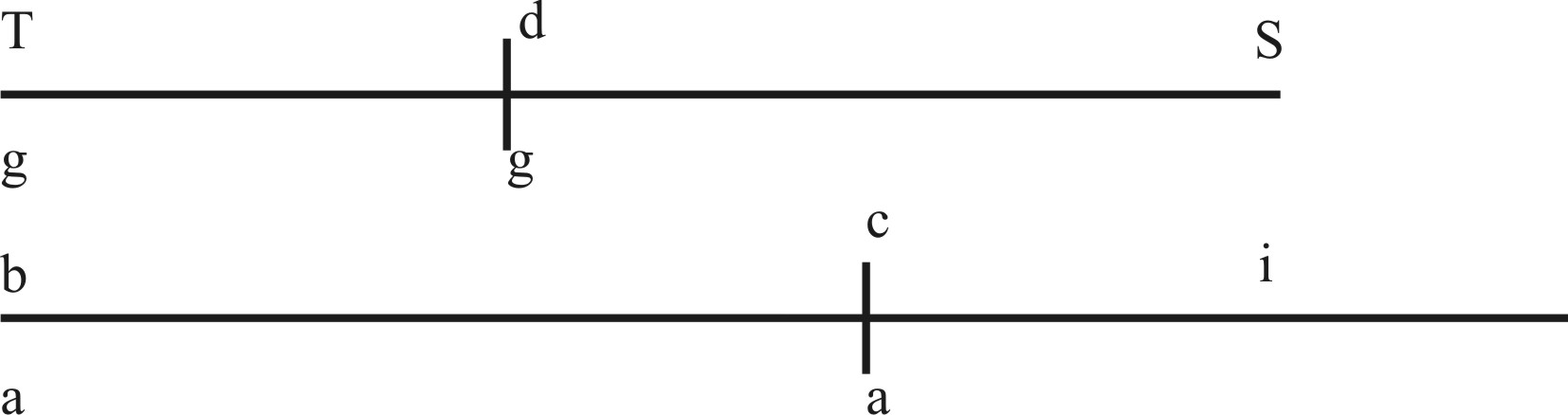
    Sit sinus totus lines TS, finus datus in eadem linea dS: certis quibusdam momentis moveatur g Geometrice a T in d. Sitque alia linea bi versus I infinita, in qua ex b moveatur a Arithmetice, eadem velocitate qua g primo cum erat in T: totidemque temporis momentis procedat a ex b fixo versus I usque in c punctum: dicetur numerus metiens bc lineam numerus artificialis sinus dS dati.
27. Unde sinus totius nihil est pro artificialis.
    Nam ex Schemate, cum g est in T faciens suam distantiam ab S sinum totum, punctus Arthmeticus a incipens in b, nusquam inde processit. Unde ex definitione distantiæ, sinus totius nullu erit artificialis.
28. Hinc etiam sequitur, quod cujuslibet dati sinus numerus artificialis, major est differentia inter sinum totum, & sinum datum? & minor differentia qua est inter sinum totum, & quantitatem eo majorem in eadem ratione, qua est sinus totius ad datum. Atque ha differentia dicuntur ideo termini artificialis.
    
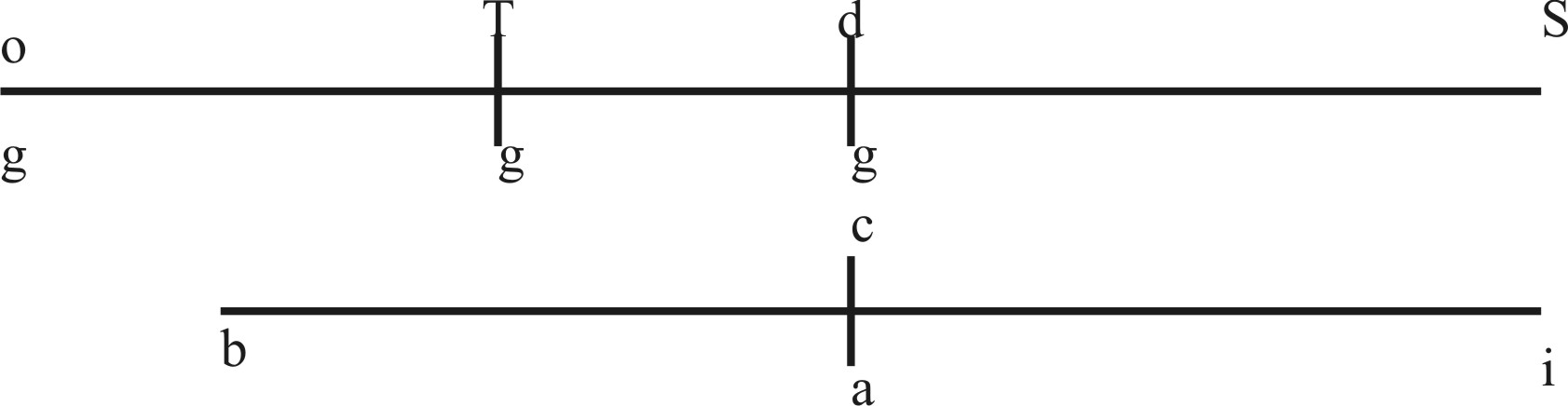
    Ut repetito præcedenti Shemate, protractaq; linea ST ultra T in o, ita ut So se habeat ad TS. ut TS as dS. Dico sinus dS numerum artificialem bc, majirem esse quam Td, & minorem quam oT. Quanto enim tempore g ab o in T fertur, tanto & g a T in d feretur (per 24) quia oT est tanta pars oS, quanta Td est lineæ TS, tantoque temopore (per definitione artificialis feretu)r & ab in c: Ita ut oT, Td, & bc sint æqualium temporum processus. At quia g inter T & o movens, velocior est quam in T, & inter T, & d tardior, in T autem g æqui velox est atque a (per 26. Sequetur processum oT quem g iam velox facit, maiorem esse: & Td precessum quoem oT quem g iam velox facit, minorem esse: & bc processum (quem punctus a mediocri suo moto totidem etiam temporis momentis perficit) medium quoddam esse inter utrumquue, quod erat demonstrandum. Numeri itaque artificialis quem bc designat, dicitur oT terminus maior, & Td terminus minor.
29. Dati itaque sinus artificiales terminos exhibere
    Ex præmissa probatur minorem terminum relinqui, ablato sinu dato a sinu toto; & maiorem terminum produci, multiplicato sinu toto in terminum minorem, & producto diviso per sinum datum, ut sequenti exemplo.
30. Unde prima Tabula primum proportionale, quod est 9999999, habet suum artificialem numerum inter termines 1,0000001, & 1.0000000.
    Nam per præmissam aufer 99.99999 a sinu toto cyphris aucto fiet unitas com suis cyphris pro minore termino: hanc unitatem cyphris auctam, & multiplicatam in sinum totum, divide per 9999999, & fient 10000001; siue (si majorem accurationem requiris) 1.00000010000001 pro majore termino.
31. Insensibili differentia distances termini ipsi, sius inter cos quiduis pro numero artificiali vero habetur.Ut in superiori exemplo, sinus hujus 9999999. artificialis numerus habetur hic 1.0000000, fiue hic 1.00000010, fiue omnium optime hic 1.0000005: quia enim ipsi termini 1.0000001 & 1.0000000, insensibili fractione utpote 2 ⁄ 10000000 differunt ad invicem: ideo &ipsi, & quicquid inter eos est, multo minus, multoque insensibiliore errore, a vero different artificiali inter hos terminos constituto.
32. Quotcumque sinuum Geometrica proportione a sinu toto deficientium, unius artificiali numero aut terminis datis, caterorum eitam dare.
    Consequitur hoc necessario incrementi Arithmetici, deceremntiGeometrici, & numeri artificialis definitiones: fiquidem per illas, ut sinus Geometrica proportione decrescunt continuo: ita interim sui artificiales, continuo Arithmetico progressu per æqualia accrescunt. Unde cuilibet sinui Geometricæ progressionis decrescendo, respondet suus artificialis Arithmeticæ progressionis crescendo: primo scilicet primus, & secundo secundus, & sic deinceps.
    Ita ut si primus artificialis, respondens primo sinui post finum totum detur, secundus artificialis erit eius duplum, tertius triplum, & sic de cæteris: donec omnes omnium artificiales innotescant, ut sequenti exemplo patebit.
33. Hinc omnium sinuum proportionalium primo Tabula, numeri artificialis inner terminos propinquos includi, & per consequens exacte satis dari possunt.
    Ut cum sinus totius artificialis sir o (per 27) & primi post sinum totum, qui est 9999999 in prima Tabula, artificialis sit (per 30) inter terminos 1.0000001, & 1.0000000: nexessario secondi post sinum totum, qui est 9999998.0000001, artificialis continebitur inter dupla illorum terminorum: scilicet inter 2.0000002 & 2.0000000: & tertij 9999997.0000003, inter eorundem tripla: scilicet inter 30000003 & 3.0000000,. Et sic in cæteris, æqualiter semper augendo terminos intervallo primorum terminorum: donec omnium proportionalium primæ Tabulæ artificiales terminos compleveris. Poteris consimili progressu, si liber, numeros ipsos artificiales exiguo & insensibili errore continuare hoc ordine: pro sinus totius artificiali, erit 0: pro primi post sinum totum artificiali, erit q.00000005 (per 31:) pro secundi, 2.00000010: pro tertij, 3.00000015. Et ita deinceps.
34. Differentia artificialium sinus totius & sinus date, est ipsius dati artificialis.
    Patet hoc quum enim sinus totius artificialis sit nihil per 27, hoc nihilo ex artificiali dati subducto, ipsum integrum artificialem dati remanere nesesse est.
35. D orum artificialium differentia, addenda est ad artificialem maioris sinus corundem, ut habeas artificialem minoris: & substrahenda ab artificiali minoris sinus, ut habeas artificialem maioris.
    Necessario hoc sit, siquidem crescunt artificialis decersecndibus sinibus atque minor est artificialis maioris sinus, & maiour minoris. Ideoque æquum est differentiam addere minori artificiali, ut habeas artificialem maiorem licet minoris sinus: & contra, auffere differentiam a maiore artificiali, ut habeas minorem artificialem licet maioris sinus.
36. Similiter proportionatorum sinuum sunt equis-differenies artificialis.
    Consequitur hoc necessario definitiones artificialium & motuum: Nam cum per eas, Geometrico decremento similiter proportionato, respondet Arithmetricum incrementum æquale semper: necessario similiter proportionatis sinibus, respondere æqui differentes artificialis & amp; numeros, & numerorum terminos concludimus. Ut in superiori exemplo primæ Tabulæ, quia similis est proportio inter primum proportionale post sinum totum 9999999.0000000, & tertium 9999997.0000003: ei quæ est inter quartum 9999996.0000006, & sextum 9999994.0000015. Ideo numerus artificialis iste 1.0000005 primi, differt ab artificialis isto 3.00000015 tertij, eadem differentia, qua artificialis iste 4.00000020 quarti, differt ab artificiali ist 6.00000030 sexti proportionalis. Eadem etiam est æqualitatis ratio inter differentias terminorum artificialium adinuicem: videlicet tam minorum inter se, quam etiam maiorum inter se, quorum sinus sunt similiter proportionati.
37. Ut trium sinuum proportione Geometrica continuatorum, quadratum medij equatur facto ex ductis innicem extremis: Ita in suis artificialibus numeris, duplum medii equatur aggregato extremorum. Unde horum artificialium duobus quibuscunque datis, tertius innoteseit.
    Quia horum trium sinuum, ratio quæ est inter primum & secundum, similis est rationi quæ est inter secundum & tertium: Ideo (oper præmissam) suorum artificialium ea est differentia inter primum & secundum, quæ est inter secundum & tertium. Sit (verbi gratia) primus artificialis linea bc expressus, secundus linea bd, tertius linea be: sintque unica linea bcbe comprehensi hoc modo
    
    sint que differentiæ cd & de æquales: horum medium bd duplotur, producta linea hac ab ultra c in f, ita ut bf sit duplum bd. Dico bf æquari utrisque lineis, bc primi artificialis, & be tertii: ab æqualibus enim bd & df, aufer æqualia cd & de: scilicet cd, abd, & de, adf: & remanebunt bc & ef necessario æqualia. Cum itaque tota bf, æqualis sit utrique bc & cf: ergo & utrique be & bc æquabitur, quod erat demonstrandum. Unde sequitur canon: I trium horum artificialium medium datum duplaueris, & hinc substraxeris extremum datum, reliquum extremorum quæsitum innorescet: & I extrema data conjunxetis, & aggregatum hoc bipartiueris, medium fiet notum.
38. Quatuor Geometrice proportionalium, ficut factum ex ducta mediorum, equatur facta ex ductu extremorum: Ita fuorum artificialium, aggregatum mediorum equatur aggregato extremorum. Unde horum artificialium tribus quibuscunque datis, quorum innoiefeit.
    Quia horum quatuor proportionalium, ratio quæ est inter primum &secundum, similis est rationi quæ est in eg tertium & quartum; Ideo (per penultime præmissam) suorum artificialium, ea est differentia inter primum & secundum, quæ est inter tertium & quartum. Tales itaque quantitates in linea bf suprascripta sumatur, ut hic, quarzum ba primum artificialem, bc secundunm, be tertium, & bg quartum referat, factis differentiis.
    
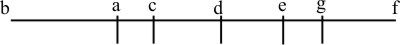
    ac & eg æqualibus: Ita ut d in medio ce postitum, in medio ag etiam poni necesse est. Iam dico aggregatum bc secondi, & be tertii, æquati aggregato ba primi, & bg quarti. Nam quia (per præmissam) duplum bd, quod est bf, æquatur utrique bc & be: quia differentiæ eorum abd, videlicet cd & de sunt æquales. Eadem ratione, & idem bf æquabitur utrique ba & bg; quia eoru differentiæ abd, videlicet ad & dg sunt etiam æquales.
    Quum itaque & aggregatum ex ba & bg, & aggregatum ex bc & be, sint iidem duplo bd, quod est bf æqualia: ergo & inter se æquabitur, quod erat demonstrandum. Unde sequitur canon, si quatuor hour artificialium, ab aggregato extremorum datorum, subduxeris alterum mediorum cognitu, relinquetur reliquum medium quod quærebatur: & si ab aggregato mediorum cognitorum subduxeris alterum extremorum cognitum, relinquetur extremum quæsitum.
39. Duorum artificialium differentia, est inter duos terminus, ad quorum maiorem se habet sinus totus, ut eorum artificialium minor sinus ad sinuum differentiam: & ad minorem terminum se habet sinus totus, ut artificialium sinus maior ad sinuum differentiam.
    
    Sit sinus totus TS, sinus duo dati dS major, & eS minor; Ultra ST signetur puncto V distantia TV, ea lege, ut ST se habeat ad TV, ut eS minor sinus, ad de differentiam sinuum. Deinde citra T versus S, signetur puncto c distantia Tc ea lege, ut TS se habeat Tc, ut ds sinus major; ad de diffentiam sinuum. Dico differentiam artificialium respndentium sinibus dS & eS, constitui inter terminus VT majorem, & Tc minorem. Nam quia ex hypothesi, ure S ad de, ita TS ad TV; & ut dS ad de, ita TS ad Tc se habent: ideo etiam ex natura (proportionalium) sequuntur duæ conclusions: Primo, quod VS se habet ad TS, ut idem T ad cS. Secundo, quod similis est ratio TS ad cS, rationi quæ est dS ad eS. Et proptera (per 36) differetia artificialium respondentium sinibus dS & eS, æqualis est differentiæ artificialia respondentium sunui toto TS, & sinui cS, At hæc differentia (per 34) est artificialis ipsius sinus cS: & hic artificialis inter terminis VT majorem, & Tc minorem (per 28 pos.) includitur: quia per primam conclusionem jam dictam, Vs major sinu toto se habet ad sinuum totum Ts, ut idem Ts ad cS. Unde necessario differenta artificialium respndentizum sinibus dS & eS, constituitur inter terminus VT majorem, & Tc minorem, quod erat demonstrandum.
40. Terminos differentia inter artificiales numerous duorum datorum sinuum exhibere.
    Quum per præmissam, sinus minor se habeat ad differentiam sinuum, ut sinus totus ad majorem terminum differentiæ artificialium: & sinus maior se habeat ad differentiam sinuum, ut sinus totus ad minorem terminum: sequetur ex natura proportionalium, quod ducto sinu toto per differentiam datorum sinuum, orietur ex product diuiso per minorem datorum, major terminus: & ex product diuiso per majorem sinuum, orietur minor terminus.
    Exemplum
    Ut sit sinuum datorum 999975.5000000, minor autem 9999975.0000300: quorum differentia .4999700 ducta in sinum totum (adjectis prius octo cypheris utrique post puctum demonstrationis gratia, liceralioquin septem sufficient) quod hinc producitur, si per majourem sinuum, scilicet per 999997.5000000 diuiseris, provenient .49997122 octo figurarum post punctum pro minore termino. Sin quod producitur, per minorem sinum, scilicet per 9999975.0000300 diuiseris, provenient .49997124 pro majore termino: inter quos (ut demonstratum est) constituitur differentia artificialium sinuum datorum. Sed quia protraction huius fractionis in octauam figuram ultra punktum, est accuratio plusquam requisite, præsertim cum in ipsia sinibus septem tantum ponantur figuræ post punctum: ideo deleta octaua illa sive ultima utriusque termini figura uterque terminus una cum ipsa artificialium differentia, in fractione .4999712 stabiliri potest, absque vel minimo scrupulo sensibilis erroris.
41. Sinuum vel numerorum naturalium, non in ipsos propotionales prima Tabula, sed prope vel inter eos cadenitium: numeros artificiales, eorumve saltem terminos insensibili differentia distantes exhibere.
    Sinui dato sinum primæ Tabulæ proximum isue minorem siue maioren nota: huius tabuli sinus terminos artificiales (per 33) quære & inuentos reserna: deinde (per præmillia) terminos differentiæ inter artificiales numeros sinus dati & sinus tabulati, sive ambos, sive (quia fere æquales sunt, ut superiori exemplo paret) eorum alterutrum quære. Hos iam inuentos, horumve alterutrum adde ad illos nuper referuantos terminos, aut ab illis subtrahe (per 8.10 & 35. prout sinus datus fuerit minor aut maior tabulato ei proximo: & qui hinc productuntur numeri, erunt termini propinqui inter quos includetur artificialis numerus sinus dati.
    Exemplum
    Ut sit sinus datus 9999975.5000000, cui sinus in Tabula proximus, est 9999975.0000300 minor dato: huius termini artificialis (per 33) sunt 25.00000025 & 25.0000000: deinde (per præmissam) differentia inter artificiales numeros sinuum dati & tabulati, est .4999712: quam (per 35) aufer ab illis terminis, quia sunt termini minoris sinus, ↦ provenient 24.5000313 & 24.5000288, termini quæstit sinus dati 9999975.5000000: cuius ipse artificialis numerus in quovis terminorum, sine optime in 24.5000300 (per 31) constitui potest absque sensibili errore.
    Aliud Exemplum
    Sit sinus datus 9999900.0000000, sinus tabulatus ei proximus 9999900.0004950, huius termini artificiales sunt 100.0000100 & 100.0000000 (per 33). Deinde differentia inter artificiales numeros illorum sinuum, erit (per præmissam) .0004950, quam (per 35) ad superiores terminos adde, & fient 100.0005050 pro maiore termino, & 100.0004950 pro minore termino, inter quos artificialis quæsitus sinus dati includitur.
42. Hinc sequitur, omnium proportionalium secundæ Tabulæ numeros artificiales exacte satis dari: seu inter terminos cognitos insensibili fractione differentes includi posse.
    Ut in præcedenti exemplo, quum numerus artificialis huius sinus 9999900 (qui est primum proportionale secundæ Tabulæ) demonstretur inter terminos hos 100.0005050 & 100.0004950 esse: necessario secundi proportionalis, numerua artificialis (per 32) erit inter hos terminos 200.0010100 & 200.0009900: &msp; tertii proportionalis, inter hos terminos 300.0015150 & 300.0014850, & c. Et tandem utlimi sinus secundæ Tabulæ, qui est 995001.22927, artificialis numerus includetur inter terminos hos 5000.0252500 & 5000.0247500. Quibus iam habitis terminis (per 31) poteris ipsos artificiales numeros eorum exqirire.
43. Sinuum vel numerorum naturalium non in ipsos proportionales secundæ Tabulæ, sed prope vel inter eos cadentium, numeros artificiales exhibere: seu inter terminos cognitos insensibili fractione differentes includere.
    Sinui dato sinuum dsecoundæ Tabulæ proximum, sive maiorem sive minorem nota, huius tabulati sinus terminos artificialises per præmissam quære: deinde per regulam proportionis, quære quartum proportionale se habens ad sinum totum: ut sinuum dati & tabulati minore se habet ad maiorem. Quod uno modo perfici poterit, ducendo dati & tabulati minorem in sinuum totum, & productum in maiorem dividendo. Altero modo faciliore, ducendo sinuum dati & tabulati differentiam in sinum totum , ↦ productum in dati & tabulati maiorem dividendo, atque quotientem ex sinu toto auferendo. At quia huius quarti proportionalis, numerus artificialis (per 36) tantum differt ab artificiali sinus totius, quantum invicem artificialis sinuum dati & tabulati different: Et quia etiam illorum differentia, eadem est cum ipso artificiali quarti per 34: Ideo artificiales terminos quarti, per penultime præmissam e Tabula prima quære, & inuentos adde ad artificiales terminos tabulati, aut ab illis subtrahe per 8. 10. & 35. prout tabulatus sinus fuerit maior aut minor dato, & producentur artificiales termini sinus dati.
    Exemplum
    Ut sit sinus datus 9995000.000000, sinus Tabulæ secundæ ei proximus est 9995001.222927, huius termini artificiales (per præmissam) sunt 5000.0252500 & 5000.0247500. Quantum deinde proportionale alterutro motum suprascriptorum quære, & fiet 9999998.7764614, cuius terminos artificiales (per 41) e prima Tabula quære, eruntque 1.2235387 & 1.2235386: quos ad superuiores terminos per 8 & 35 adde, fientque pro terminis artificialibus dati 5001.2487888 & 5001.2482886. Unde & numerus inter hos Medius, qui est 5001.2485387, optime (per 31 pos.) pro ipso artificiali numero sinus 9995.000 dati statuitur absque sensibili errore.
44. Hinc sequitur, omnium proportionalium prima Columæ tertia Tabula, numeros artificiales exacte satis dari: seu inter terminos cognitos insensibili fractione differentes includi posse.
    Nam quum per præmissam, huius 9995.000 (qui est primus sinus infra sinum totum, ex proportionalibus primæ Columnæ tertiæ Tabulæ) numerus artificialis sit 5001.2485387 absque errore sensibili: secundui proportionalis scilicet 9990002.5000, numerus artificialis (per 32) erit 100002.497974. Et sic in cæteris, progrediendo usque ad ultimum eius columnæ sinum 9900473.57808 cuius, pari ratione artificialis numerus erit 100024.9707740: eiusque termini 100024.9657720 & 100024.9757760 erunt.
45. Numerorum naturalium, seu sinuum non in ipsos proportionales prima Columna tertia Tabula, sed prope vel inter eos cadentium numeros artificiales exhibere: seu inter cognitos terminos insensibili fractione differentes includere.
    Sinui dato sinum primæ Columnæ tertiæ Tabulæ proximum, sive minorem sive maiorem nota; huius tabulati terminos artificiales per præmissam quære: deinde quartum proportionale se habens ad sinum totum, ut sinuum dati & tabulati minor ad maiorem, per unum ex modis in penultime præcedente descriptis quære; huius quarti ita inventi terminos artificiales (per penultime præmissam) e secunda Tabula quære, & inventos adde ad terminos tabulati sinus superius inventos, aut ab illis subtrahe (per 8., 10. & 35.) & producentur artificiales termini sinus dati. Exemplum
    Ut sit sinus datus 9900000, proportionalis sinus primæ Columnæ tertiæ Tabulæ ei proximus, est 9900473.97808, cuius termini artificiales per præmissa sunt 100024.9657720 & 100024.9757760. Quartum inde proprtionale erit 9999521.6611850, cuius termini artificiales (per 43 e secunda Tabula desumpti) sunt 478.3502290 & 478.3502812; quibus terminis ad terminos superiores tabulati (per 8 & 35) additis, provenient termini 100503.3260572 & 100503.3160010, inter quos necessario cadit artificialis numerus quæsitus. Unde numerus inter hos medius, qui est 100503.3210291, pro vero artificiali numero sinus 9900000 dati, statui absque sensibili errore potest.
46. Hinc sequitur, omnium proportionalium tertia Tabula numerer artificialis exacte satis dari.
    Nam quum (per præmissam) 100503.3210291, sit artificialis primi sinus secundæ Columnæ, qui est 9900000, cæterisque primireliquarum columnarum sinus eadem proportione progrediantur, necessario (per 32 & 36) eorum numeri artificiales eadem semper differentia crescunt, additis 100503.3210291 antedecenti artificiali, ut fiat sequens. Habitis ergo sic primis artificialibus cuiusque columnæ; atque per penultime præcenetem omnibus artificialibus primæ columnæ datis, elige tibi, an mavis simul eiusdem columnæ omnes artificiales condere, addendo semper ad superiorem artificialem cuiuslibet columnæ, hanc artificialium differentiam 5001.2485387, ut fiat proxime inferior euisdem columnæ artificialis: An mavis simul eiusdem ordinis omnes artificiales, scilicet omnes secundos singularum columnarum artificiales, inde omnes tertios, inde quartos, & sic reliquos constituere, addendo semper 100503.3210291 cuilibet artificiali præcedentis columnæ, ut eiusdem ordinis sequentis columæ artificialis proveniat. Utrovis enim modo, omnes onmium huius Tabulæ proportionalium habentur artificiales, quorum ultimus, & ad sinuum 4998609.4034 congruens, est 6934250.8007528.
47. Omnibus tertia Tabula naturalibus numeris, ascribendi sunt sui artificiales, ut tertia Tabula integra fiat & perfecta: quam posthac semper radicalem vocabimus.
    Hæc huius Tabulæ conscriptio sit constituendo columnas numero & ordine quibus per 20 & 21 describuntur: & divisa in duas series:

    Radicalis Tabulæ

    Columna prima.		Columna secunda.
    Naturales.	Artificiales.	Naturales.	Artificiales.
    10000000.0000	0	9900000.0000	10503.3
    9995000.0000	5001.2	9895050.0000	105504.6
    9990002.5000	10002.5	9890102.4750	110505.8
    9985007.4987	15003.7	9885157.4237	115507.1
    9980014.9950	20005.0	9880114.8451	120508.3
    & c. iusque ad	usque ad	usque ad	usque ad
    9900473.5780	100025.0	9801468.8423	200528.2
    & cætera usque ad		Columna 69.
    		Naturales.	Artificiales.
    		5048858.8900	6834225.8
    		5046333.4605	6839227.1
    		5043811.2932	6844228.3
    		5041289.3879	6849229.6
    		5038768.7435	6854230.8
    		& tandem	usque ad
    		4998609.4034	6934250.8

    quarum prima, proportionalia illa Geometrica, quæ sinus numerosque naturales nominamus: secunda, hos suos artificiales Arithmetice per æqualia progredientes continuat. Duobus tamen (compendii, gratia) animaduersis: Primoo quod illis omnibus artificialibus, unam post punctum relinqui figuram satis sit, cæteris sex novissimis jam rectis: quas tamen I initio neglexisses error inde frequenti multiplicatione priorum tabularum, accrevisset in hac tertia intollerabilis. Secundo, I secunda post punctum figura excedat quaternarium: figura prima, quæ sola post punctum relinquitur, est initate augenda. Ut pro 10002.48 &c. rectius est ponere 10002.5, quam 10002.4: & pro 100035001, aptius ponimus 1000.4, quam 1000.3. Itaque eo situ procedat jam radicalis Tabula quo præmittitur.
48. Perfecta iam radicali Tabula, ex ea sola Tabula artificialis numeros excerpimus.
    Ut enim priores duæ Tabulæ ad constitutionem tertiæ in inserviebant; Ita tertia hæc radicalis ad principalem artificialem Tabulam, quam facillime & absque errore sensibili condendam inseruit.
49. Sinuum majorum quam 999700, artificiales numeros facillime exhibere.
    Fiet hoc, sola subtractione sinus dati a sinu toto. Nam per 29 artificialis numeros sinus 9996700, est inter terminos 3300 & 3301; qui quidem termini (quia invicem unitate tantum differunt) a suo artificiali vero, non possunt errore sensibili, vindelicet maiore unitate differre. Unde ipse terminus minor 3300, qui sola subtractione habetur, pro ipso artificiali capi potest. Eaddem necessario ratio est de omnibus sinibus hoc majoribus.
50. Sinuum omnium intra limites Tabula radicalis comprehensorum, artificiales exhibere.
    Sinuum dati, & tabulati ei proximi, differentiam duc in sinum totum; productum partire per facillimum divisiorem, qui vel sit sinus datus, vel tabulatus ex proximus, vel inter utrumque utconque constitutus; & producetur differentiæ artificialium aut terminus major, aut minor, aut intermedium quidpiam (per 39) quorum nullus a vera artificialiu differentia errore sensibili differer, propter propinquitatem numerorum Tabulæ. Et ideo hunc eoreum quemcunque productum (per 35) adde, ad artificialem tabulati in tabula repertum, si sinus datus sit minor tabulato sinu: alioquin illum productum ex hoc tabulati artificiali subtrahe, & provenier dati sinus numerus artificialis quæsitus.
    Exemplum.
    Ut, sit sinus datus 7489557, cuius quætitur artifioialis. Sinus tabulatur ei proximus est 7590786.6119, hinc aufero illam adiectis cypheris sic 7489557.0000, relinquentur 1229.6119; quæ ducta in sinum totum, divido per numerum facillimum, qui sit vel 7489557.0000, vel 7400786.6119, vel optime per quippiam inter eos constitutum, ut pote per 7490000, & facillima divisione provenient 16401: quæ (quia datus sinus minor est tabulato) adde ad artificialem tabulati, videliecet ad 2890751 4 ⁄ 5: sed quia Tabula principalis nec fractiones admittit, nec quicquam ultra punctum, ponimus pro illo 2890752, qui est artificialis quæsitus.
    Aliud Exemplum.
    Sit sinus datus 7071068.0000, sinus tabulæ ei proximus erit 7070084.4434, quorum differentia est 9835566, quibus ductis in sinum totum, productum divide optime per 7071000, quæ sunt inter sinus datum & tabulatum, provenient inde 1390.9: quæ (quia sinus datus excedit tabulatum ei proximum) subtrahatur ex artificiali numero tabulati in tabula reperto, scilicet a 3467125.4, remanebit 3465734.5. Unde 3465735 ponitur pro artificiali quæsito sinus 7071068 dati. Itaque hæc libertas divisorem eligendi miram parit facilitatem.
51. Omnes sinus in proportione dupla, habent 693 1469 22 pro differentia suorum artficialium.
    Quia enim omnis sinus ad suum dimidium eadem est ratio, quæ est totius ad 50000000: ideo (per 36) differentia artificialium cuiusque sinus & sui dimidii, est eadem cum differentia artificialium sinus totius, & sui dimidii 50000000. At eadem est differentia artificialium sinus totius, & sinus 5000000, cum ipso artificiali sinus 50000000 (per 34) cuius 50000000, artificialis (per præmissam) erit 6931469.22. Ergo & idem numerus 6931469.22 erit differentia omnium artificialium, quorum sinus sunt in Proportione dupla: & per consequens duplum eius, scilicet 13862938.44, erit differentia omnium differencialium, quorum sinus sunt in ratione quadrupla: & triplum eius, vindilicet 20794407.66, erit differentia omnium artificialium, quorum sinus sunt in ratione octupla.
52. Omnes sinus in proportione decupla, habent 23025841.34 pro differentia suorum artificialium.
    Nam per penultime præmissam, sinus 80000000 habet artificialiem suum 2231434.68: & per præmissam, differentia inter artificiales sinuum 80000000, & suæ octavæ partis 1000000, est 20794407.66: Unde per additionem fiunt 23025842.34, pro artificiali sinus 1000000: & quum ad hunc sinus totus sit decuplus, omnes sinus in ratione decupla, eandem illam differentiam 23025842.34, inter suos artificiales habebunt, eadem causa & ratione, quam iam in dupla proportione per præcedemtem exposimus, quod probandum erat. Et per consequens, centuplæ proportioni respondebit huius artificalis duplum, quod est 46051684.68, pro differentia artificialium: Et eiusdem triplum, quod est 69077527.02, erit differentia omnium artificialium, quorum sinus sunt in ratione millecupla. Et sic de ratione 10000², & aliis, ut infra.
53. Unde omnes sinus in ratione composita ex duplo & decuplo, habens artificiales suos differentia 6931469.22, & differentia 23025842.34 respective differentes.
    Ut in tabella subsequento conspicere licet.

    Sinuum proportiones datæ.	Artificialium respondentes differentiæ.	Sinuum proportiones datæ.	Artificialium respondentes differentiæ.
    Dupla	6931469.22	8000pla	89871934.68
    Quadrupla	13862938.44	10000pla	92103369.36
    Octupla	20794407.66	20000pla	99034838.58
    Decupla	23025842.34	40000pla	105966307.80
    20pla	29957311.56	80000pla	112897777.02
    40pla	36888780.78	100000pla	115129211.70
    80pla	43820250.00	200000pla	122060680.92
    Centupla	46051684.68	400000pla	128992150.14
    200pla	52983158.90	800000pla	135923659.36
    400pla	59914623.12	1000000pla	118155054.04
    800pla	66846092.34	2000000pla	145086523.26
    Millecupla	69077527.02	4000000pla	152017992.48
    2000pla	76008996.24	8000000pla	158949461.70
    4000pla	82940465.46	10000000pla	161180896.38

54. Omnium sinuum ultra limites radicalis Tabula exclusorum, numeros artificiales investigare.
    Hoc facile sit, sinum datum multiplicando per 2, 4, 8, 10, 20, 40 80, 100, 200: vel per alium quemuis proportionis numerum hac tabella expressum, dones producatur numerus, qui intra limites radicalis tabulæ contineatur. Huius iam sub Tabula comprehensi artifialem (per 50) quære, cui acquisito adde tandem differentiam artificialem, quam Tabella indicat priori convenisse multiplicationi. Exemplum.
    Quæsitur, quem artificialem sinus 378064 habeat; is eum ultra limites Tabulæ radicalis excludatur, per numerum aliquem proportionum præcedentis tabellæ, utpote per 20 ducatur, fietque 7561280, cuius iam intra Tabulam cadentis artificialem (per 50) quære, fietque 2796444.9, ad quem adde differentiam in Tabella inventam convenientem vigecuplæ proportioni, quæ est 29957311.56, fientque 32752756.4. Unde 32752756 est artificialis quæsitus, sinus 378064 dati.
55. Ut dimidium sinus totius, se habet ad sinum dimidii alicuius arcus; Ita sinus complementi eiusdem dimidii, ad sinum totius arcus.
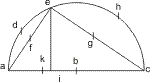    Sit sinus totus ab, dupletur & sit abc; hac diametro fiat semi-circulus, in quo signetur arcus ille ac, bifariam in d divisus: eius ergo dimidii quod est de, extendatur complementum ab c versus c, quod sit arcus eh, cui & hc necessario æquatur: quia deh quadrans æquatur reliquo quandranti arcuum ad & hc. Proinde ducantur linea ei perpendicularis ad aic, quæ ideo sinus est arcus ade: & linea æ, cuius dimidium fe, est sinus arcus de, qui est dimidium arcus ade: & linea ec cuius dimidium eg est dimidium arcus ade: & linea ec, quius dimidium eg est sinus arcus eh, & ideo est sinus complementi arcus de: dimidium autem sinus totius ab sit ak. Dico ut ak se habet ad ef, ita eg ad ei se habebit: duo enim trianguli cea, & cie, æqui-anguli sunt: quia ice, & cea rectus est, ille ex hypothese, hic, quia in peripheria est, & semi-circulum occupat. Ideoque ut ac hypotenusa trianguli cea, ad eius minus latus æ; ita se habet ce hypotenusa triang. cie, ad eius minus latus ei. Et quum totum ac se habeat ad æ, ut totum ecc ad ei: sequetur inde dimidium ac, quod est eg, se habet ad ei. Et denique cum iam totum ab est ad totum æ, ut eg ad ei. Concludimus necessario dimidium ab, quod est ak, se habere ad dimidium æ, quod est fe: ut eg se habet ad ei, quod erat demonstrandum.
56. Duplum artificialis arcus 45 graduum, est artificialis dimidii sinus totius.
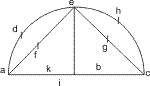    Repetitio præcedenti Schemate sit casus talis, quod æ, & ec sint æquales. In hoc casu cadet i in b, eritque ei sinus totus, atque ef, & eg æquabuntuer; eorumque quivis sinus est 45 graduum. Et quia (per præcedentem) quæ est proportio dimidii sinus totius ak, ad ef sinum 45 graduum: ea est etiam propotio eg sinus quoque 45 graduum, ad ei iam sinum totum. Ideo (per 37) duplu, artificialis sinus 45 graduum, æquale est artificialibus extremorum, scilicet sinus totius, & æquale dimidii. At Horum amborum artificiales, sunt tantum artificialis alterius eorum, scilicet dimidii sinus totius: quia reliqui scilicet ipsius sinus totius (per 27) artificialis nullus est. Necessario igitur duplum artificialis arcus 45 graduum, est artificialis dimidii sinus totius, quod erat demonstrandum.
57. Aggregatum ex artificiali dimidii sinus totius, & artificiali cuisque arcus, æquatur aggregato artificialium dimidii eius arcus, & complement huius dimidii. Unde artificialis huius dimidii arcus haberi potestm cæterorum trium artificialibus datis.
    Quia per penultime præmissam, dimidium sinus totius proportionatur ad sinum dimidii alicuius arcus, ut sinus complementi eiusdem dimidii arcus, ad sinum totius arcus: Ideo (per 38) aggregatum artificialium duorum extremorum, scilicet artificialis dimidii sinus totius, & artificialis cuiusque totalis arcus, æquabitur aggregato artificoialium mediorum, videlicet artificialis dimidii eiusdem arcus, & artificialus complementi huius dimidii. Unde & per eandem 38, si addideris artificialem dimidii sinus totius (per 51, vel per præmissam inventum) ad artificialem cuiusuis totalis arcus datum: & hinc subtraxeris artificialem complementi dimidii prioris arcus datum, relinquetur ipse artificialie petitus eiusdem dimidii arcus; quæ erant demonstrada.
    Exemplum.
    Sit artificialis dimidii sinus totius (per 51) 6931469, sitque arcus totalis 69 graduum & 20 minutorum, cuius artificialis sit 665143 datus: totalis arcus dimidium est 34 graduum & 40 minutorum, huius artificialum quæro. Complementum huius dimidii arcus est 55 graduum, & 20 minutorum, cuius artificialis sit 1954370 datus: addo itaque 6951469 ad 665143, & fiet aggregatum 75966121: ex quo aufero 1954370, & relinquetur 5642242 artificialis quæsitus, arcus 34 graduum & 40 minutorum.
58. Datis artificialibus omnium arcuum non minorum 45 gradibus, omnium arcuum minorum artificialis facillime habentur.
    Ex artificialibus arcuum omnium non minorum 45 graduum per hypthesin datis, habebis per præmissam, artificiales reliquorum omnium arcuum decrescentium usque ad vigesimum secundum gradum cum semisse. Ex quibus iam habitis, artificiales similiter reliquorum arcuum usque ad 11 gradus & 15 minuta habebuntur. Et ex his rursus, artificales omnium arcuum utque ad 5 gradus & 38 minuta. Et ita deinceps in primum usque ad minutum.
59. Tabulam Artificialem condere.
    Paginæ præparentur quadraginta quinque longiusculæ, ut præter margines superiorem & inferiorem, sexaginta etiam lineas onmerales capere valeant. Paginarum quælibet lineamentis transversis in 20 spatia æqualta dividatur: spatiorum quodvis tres lineas numerales capere valeat. Inde aliis lineis descendentibus dividatur pagina quævis in columnas septem, interposity duplici linea inter columnas secundam & tertiam, & inte quintam & sextam: inter cæteras vero simplex ponatur linea. Prima pagina in fronte superiore lævorum, supra tres primas columnas superscribatur hoc totulo ❘ 0 Gradus ❘ & superscibatur inferius & dex trorsum sub tribus ultimis columnis sic ❘ 89 Gradus ❘ Secunda pagina superscribatur lævorsum sic ❘ 1 Gradus ❘ & subscribatur dextrorsum sic ❘ 88 Gradus ❘ Et ita cu cæteris paginis procedendo, ut suprascripti infrascriptis additi, quadrante uno minus sive 89 gradus semper compleant. Inde prima columna per singulas paginas titulum hunc suprascriptum habeat ❘ Minuta gradduum suprascriptorum ❘ Secunda columna hoc titulo superscribatur ❘ Sinus arcuum finistrorum ❘ Tertia columna hoc titulo superscribatur ❘ Artificiales arcuum dextrorum ❘ Quarta columna hoc titulo & superscribatur & subscribatur ❘ Differentia inter artificiales complementorum ❘ Quinta columna subscribatur hac subscribatur ❘ Artficiales arcuum dextrorum ❘ Sexta columna subscrubatur hac subscriptione ❘ Sinus arcuum dextorum ❘ Septima columna subscribatur hac subscriptione ❘ Minuta graduum infra scriptorum ❘ Primæ deinde columnæ inserantur numeri minutorum ab 0 ad 60 progrediendo. Septimæ etiam columnæ inserantur numeri minutorum a 60 ad 0 decrescendo: ea lege, ut primæ & septimæ columnæ bina quæævis minuta in eadem linea opposita, gradum intergrum seu 60 minuta perficiant. Exempli gratia, 0 ad 60, & 1 ad 59, & 2 ad 58, & 3 ad 57, &c opponatur. Atque inter bina quæque viginti lineamentorum transversorum, tres numeri in quodlibet intervallo cuiuslibet columnæ contineatur. In secunda columna ponantur numeri sinuum, respondentium gradubus supra, & minutiis a latere lævorsum in eadem linea positis. In sexta etiam columna ponantur numeri sinuum, respondentium gradibus infra, & minutiis a latere dextrorsum in eadem linea positis. Hos sinus suppeditabit tibi communis sinuum REINHOLDI tabula, vel si qua exactior. His peractis, omnium sinuum inter sinum totum & suum dimidium, artificiales per 49 & 50: cæterorum vero sinuum 45 gradum artificiales, per easdem 49 & 50 computato: ex quibus jam habitis, omnes reliquorum arcuum minorum 45 gradibus artificiales, per præmissam quam facillime acquires. Quibus omnibus artificialibus utcunque computatis, in tertia columna locabis artificiales numeros respondentes gradibus supra, & minutiis a latere sinistro, suisque sinibus lævorsum in eadem linea positis. Similiter & in quinta columna locabis numeros artificiales respondentes gradibus infra, & minutiis a latere dextro, suisque sinibus dextrorsum in eadem linea positis. Media tandem columna sic perficitur: numerum quemque articialem dextrum, ex artificiali sinistrorsum in eadem linea posto aufer, notata differentia in eadem linea interrutrumque, donec totam mediam columnam compleveris. Hanc Tabulam nos ad singula minuta computavimus, atque eriditis (quibus plus sit otii) eius exactiorem elimationem, ut & Tabulæ linuum emendationem relinquimus.

Epitome Tabulæ artificialis aliter condendæ.

60. Quia nonnumquam artificiales per 54 inventi, differunt ab artificialibus per 58 inventis; ut huius sinus 378064, numerus artificialis per illam est 32752756, per hanc vero est 32752741 arguitur quibus in locis Tabula sinuum vitiosa esse. Qua propter consulo eruditis (quibus forsan discipulorum & computistarum copia sit) ut Tabulam sinuum exactiorem & maioris numeri edant, utpote cuius sinus totus sit 1000000000, scilicet octo cyphrarum prater untitatis figuram, cum prior sinus totus septem tantum constet. Deinde ut Tabula nostra prima contineat cntum numeros, progradientes in ea proportione, qua est inter hunc novum sinum totum, & sinum eo minorem unitate, utpote inter 100000000, & 999999999.
    Secunda Tabula contineat etiam centium numeros, in ea proportione, qua est inter hunc novum sinum totum, & numererum eo minorem centenario, scilicet inter 100000000, & 99999900.
    Tertia Tabula qua & radicalis dicitur, trigintaquinque columnas, & centum numeros in qualibet columna continet. Centum numeri eiusdem columna progrediantur in ea proportione, qua est decem millium, ad numererum eo minorem unitate, videlicet 100000000 ad 99990000. Tringinta quinque primi inter se, aut securidi, aut tertii, aut cæteri eiusdem ordinis omnium columnarum inter se progrediuntur es proportione, qua est 100 ad 99, aut sinus totius 100000000 ad 99000000. In his suisque artificialibus inveniendis & continuandis, observentur regula cætera præcedentes. Atque ex completa sic radicalis Tabula omnium sinuum inter sinum totum & sinum 45 graduum artificiales, exactissime per 49 & 50 reperies: atque ex artificiali arcus 45 graduum duplato, habebis artificialem dimidii sinus totius per 56. Et tandem ex his iam habitis, cæteros artificiales per penultime pracedentem exquiret; quos in ordinem Tabula per præcendentem rediges, & fiet Tabula, omnium cetre Mathematicarum Tabularum præstantissima & ad usus praclarismos parata.

Englische Übersetzung von William Ræ Macdonald (1889) bei: Open Library.