Populäre Irrtümer bezüglich der Kepler-Gleichung
Ganz geniale Besucher meiner Website stellen fest, dass die Zuordnung der Winkel nicht richtig sein kann, weil sie ein Beispiel gefunden haben, bei dem die Kepler-Gleichung offensichtlich nicht richtig ist.
Sie betrachten folgende Skizze:
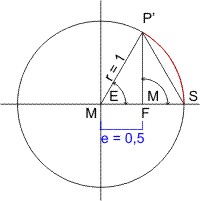
Der Kreis hat den Radius r = 1, der Abstand des Punktes F vom Mittelpunkt ist e = 0,5, P' ist ein Punkt auf dem Kreis senkrecht über F. das Dreieck MP'S ist gleichseitig, und E = 60° = 1⁄3·π. Der Winkel ∠P'MS = M ist offensichtlich ein rechter, M = ½·π.
Nun setzen diese Naseweise die Werte für E und M in die Kepler-Gleichung ein:
M = E - (e/r)·sin E = 1⁄3·π- ½·sin E = 1,047 - ½·0,866 = 0,607 ≠ 1,571.
Daraus folgt der Trugschluss, entweder ist die Kepler-Gleichung falsch, oder meine Zuordnung der mittleren Anomalie M als Winkel bei F ist nicht richtig. Das erste anzunehmen trauen sich diese Naseweise dann doch nicht...
Wo liegt der Denkfehler der Naseweise?
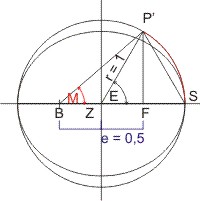Nach Kepler ist die mittlere Anomalie M der Winkel, den, von der Sonne im Brennpunkt B aus gesehen, der Punkt P' von sonnenfernen Scheitel S aus zurück gelegt hat, also der Winkel P'BS. Und der ist - offensichtlich - nicht ½·π!
Carl Friedrich Gauss bezeichnet in seinem Werk Theoria Motus Corporum Coelestium in Sectionibus Conicis Solem Ambientium (1809) die Kepler-Gleichung eine transzendente Gleichung. (Eigentlich sollte Carl Friedrich Gauss auch unverdächtig sein!) In der Übersetzung des Werkes von Carl Haase (1865) heisst es:
"Die Gleichung XII, E = M + e sin E, die transcendent ist und eine directe Auflösung nicht zulässt, wird durch Versuche aufgelöst, indem man mit einem genäherten Werthe von E beginnt, der durch geeignete, so oft wiederholte Methoden corrigirt wird, bis er jener Gleichung genau Genüge thut, d. h. entweder mit aller der Genauigkeit, welche die Sinustafeln zulassen, oder doch mit der, welche dem vorgesteckten Ziele entspricht."
Leider gibt es nur in der
englischsprachigen Wikipedia eine Definition der transzendente Gleichung:
"A transcendental equation is an equation containing a transcendental function. Such an equation cannot be solved for one factor in terms of another." Als Beispiel wird angeführt: x = cos(x).
Also: eine transzendente Gleichung enthält die Variable (hier E) auf beiden Seiten des Gleichheitszeichens, und auf einer Seite eine transzendete Funktion dieser Variable (Beispiele sind Exponentialfunktionen, Logarithmenfunktionen und Winkelfunktionen).
Kepler war ja interessiert an der Länge des in der Skizze rot markierten Bogens aus der Sicht des Punktes F (Brennpunkt der Ellipse), denn er wollte den Ort eines Planeten auf seiner elliptischen Bahn um die Sonne berechnen. Leider konnte er seine Gleichung nur interativ lösen, weil sie transzendet ist; er erkannte aber in seiner Astronomia Nova, dass es durch Differentialrechnung gelingen müßte:
…Itaque diffentientibus aequationibus a vera, coepi rursum accusare verissimas has distantias AE & librationem Planetae LE, de crimine, cujus falsa mea methodus, quae I pro F spectabat, erat rea. … (Caput LVIII, Astronomia Nova)
Es macht also gar keinen Sinn, die Kepler-Gleichung durch Einsetzen von Werten für E, M und e/a berechnen zu wollen. Es ist mathematisch schlicht falsch.