Auszug aus:

Clavis Universi Trigonometrica: per quam Coeli ag Terræ adyta recludi.

ISAGOGE PROSTHAPHÆRETICA

Compendium illud TRIGONOMETRICUM, quod Cl.mus LONGOMONTANUS, in Astronomia Danica TRIBUS Regulis succincte proposuit, aliquanto uberius dilatans, & omnium casuum, qui occurrere possunt varietates, per SEPTEM Regulas, singulisq; addita exempla, dilucide explanans.

INVENTUM hoc sane ingeniosum, & ex ipsis Geometriæ fundamenris exstructum, uti sexcenta alia in Astronomicis feliciter partim restituta, partim recens inventa, debetur primo omnium Generoso illi Tychoni Brahæo, cujus nomen si dixero, satis eum laudavero. Is communicata cum Paulo Wittichio Uratislaviense, domestic suo opera, Studiosis adolescentibus, qui ipsi ad negocia Mathematica in celeberrimo illo URANIBURGO, dum (heu) erat, inserviebant, ad Sphæricorum triangulorum, ex observationum Coelestium ratiocinijs subinde enascentium, expeditriorem άνάλυσιν (analysin) nonnulla hujus modi subsidia præscripsit quæ Potentissimi Regis Daniæ Christiani IV. in Academia Hafniensi Mathematicus excellentiss Christianus Sever. Longomontanus generaliora efficiens, TRIBUS Regulis pleraq; omnia ad Calculum Trigonometricum spectantia comprehendit. Quia vero istæ ob occurrentes datorum trigonicorum varietates aliqUanto sunt breviores, q uam ut inexercitatis primo aggressu satisfacere, & ad Omnem Calculi fortunam instruere possint, nos hac in re doctiss. cujusdam viri monita secuti, in SEPTEM REGULAS, isto ordine in singulis totius Trigonometriæ nostræ exemplis observato, bona illius Amici nostri omnium veterrimi, omnium carissimi, cum venia majoris perspicuitatis ac preciosiss temporis usuræ gratia amplificavimus.

PRIMA REGULA.

Si fueritin datorum dispositione ex Problematis præscripto, ut sinus totus ad sinum alicujus: Ita sinus alterius cujusdam arcus ad aliud, seponantur duo illi arcus, tanquam dati, qui ad ϖροσϑαφαιρέσιων (prosthaphairesion) requiruntur, minorq; addatur complemento majoris ad Quadrantem, & aggregati quæratur Sinus. Porro triplicis Cautelæ observatione opus erit.

PRIMA CAUTELA. Si minor arcus complemento majoris fuerit æqualis (quod fiet, quando duo arcus dati conjunctim Quadrantem conficiunt) semissis qæsiti sinus erit Quartus numerus proportionalis quæsitus.

Exemplum. Dantur trianguli αβγ Sphærici rectang. Basis αγ 66 gr. 29 pr. & angulus αγβ 23 gr. 31 pr. Quæritur per I. Prob. Sphær. Crus αβ

Vulgaris operatio. Ter. prop.

Per ϖροσϑαφαιρέσιν (prosthaphairesin) res ita habet: datiq; arcus conjunctim Quadrantem complent.

Altera Cautela: Si minor arcus fuerit minor complemento majoris (quod accidit quando dou arcus dati conjunctim sunt Quadrante Circuli minores) subtrahatur minor arcus ex complemento mahoris, ut emergat eorum arcuum, qui primum simul additi erant, differentia, cujus Sinus quæratur, isq; auferatur a superioris aggeragti Sinus. Hujus resisui semissis erit Quartus numerus quæsitus.

Exemplum. Triangulo αβγ Spær. rectang. nota sunt, basis αγ 30 gr. & angulus γαβ 33 gr. 41 pr.: Quæsitur per I. Prob. Sphær. Crus γβ.
Secundum vulgar. operat.

Ter. pro.	γβα 90 gr.		γβα 33 gr. 41 pr.		αγ 30 gr.
Si. t. 10,000,000			Si. 5,546,024		Si. 5,000,000
Quartus 2,773,012. Sinus: Ejus arcus 16 gr. 6 pr. Crus γβ

Quoniam arcus dati conjunctim sunt Quadrante Circ. minores compendium Prosthaphæreticum tale est.

Tertia Cautela: Si deniq; minor arcus fuerit major Complemento majoris arcus (idq; eveniet quando duo arcus dati conjunctim sunt Quadrante majores.) tollatur complementum majoris ex arcu minore, ut eorum arcuum, qui simul collecti fuerunt, habeatur differentia, cujus quæratur Sinus, isq; adjiciatur ad superioris aggregati Sinum. Hujus enim summæ semissis represæntabi numerum Quartum proport. quæsitum.

Exemplum. in triang. αβγ Sph. rect. dantur, Basis αγ 20 gr. 56 pr. & angulus αγβ 71 gr. 15 pr. Per I. Prob. Sphær. datur etiam Crus αβ. Juxta Vulg. operat.

Ter. prop. αβγ 90 gr.		αγ 29 gr. 56 pr.		αγβ 71 gr. 15 pr.
Si. t. 10,000,000		Si. 4,989,920		Si. 9,496,301.
Quartum 4,725,105. Sinus: Ejus arcus 28 gr. 12 pr. Crus αβ

Siquidem dati arcus Quadrante sunt majores, Calculus Prosthaphæreticus ita se habet.

Arcus major 71 gr. 15 pr.	Compl. 18 gr. 45 pr.
Arcus minor 29 gr. 56 pr.	Compl. 29 gr. 56 pr.
	Aggreg. 48 gr. 41 pr.	Sinus 7,510,722.
	Differ. 11 gr. 11 pr.	Sinus 1,939,490.
		Summa 9,450,212.
		Semis 4,725,106.
		Sinus, cum ante invento consentiens.

SECUNDA REGULA.

Si, Sinu toto primum locum obtinente in Reg. proportionum, reliqui duo numeri,aut horum alteruter, non fuerint Sinus recti, sed vel Sinus Versi, vel Tangentes, vel Secantes, inquirendi sunt in Canone Sinuum illis numeris, tanquam forent Sinus recti, correspondentes arcus, & potto juxta præcedentem Regulam πρἃξις (praxis) instituenda. Hic tamen rursum duæ Cautelæ probe notentur.

Prior Cautela: Quando illi numeri singuli Sinum totum excesserint, a parte dextra seu sine illorum abjiciendæ sunt tot figuræ, quot satis sunt, ut residuum Sinu integro minus fiat & post juxta Primam Regulam procedendum.

Altera Cautela: Quot characteres a numeris abjecti fuerint, tot Siphræ invento Quarto ad finem rursus annectantur, & tunc numerus ita auctus, erit vel Sinus Versus, vel Tangens, vel Secans. Qualis nimirum juxta Problematis propositi leges Quartus ille numerus esse debet, cuius arcus excompetenti Tabula inquiratur.

Exemplum Primum, in quo adhibitur Sinus versus.

Dantur Trianguli αβγ Sphær. obliquang. anguli duo, βαγ 44 gr. 12 pr. βγα 23 gr. 31 pr. & latus αγ 40 gr. Ex his per XXIV. Prob. Sphær. datur etiam angulus tertius αβγ. Juxta secundum enim modum ejus per vulgarem πραγματείυν (pragmatyn) ita se habet Calculus.

Ter. prop. 90 gr.		βαγ 44 gr. 12 pr.		αγ 40 gr. 2 pr.
Si. t. 10,000,000		Si. R. 6,971,651.		Si. V. 2,343,296
Quartus 1,633,664.		Rursum sunt Ter. prop.
90 gr.		βγα 23 gr. 31 pr.
Si. t. 10,000,000		Si. R. 3,990,159.		1,633,664.

Quartus 651,858 differentia Sinuum versorum quasiti anguli & differentia alterius utrius anguli, & relsiqui ad semicir. complementi. Anguli autem βγα 44 gr. 12 pr. Complem. ad semicirculum est 135 gr. 48 pr. a quo sublatus angulus βαγ 23 gr. 31 pr. relinquit differentiam 112 gr. 17 pr. cuius sinus versus 13,791,870. Huic addita differ. inventa 651,858 componit Sinum versum 14,443,728 cujus arcus 116 gr. 23 pr. angulua quæsitus αβγ.

Per ϖροσϑαφαιρέσιν (prosthaphairesin) resita conficitur.

Quoniam tertius numerus prioris vulgaris Operationis est sinus versus 2,343,296 proinde imaginabimur cum esse Sinum rectum, cui ex Canona Sinuum debetur arcus 13 gr. 33 pr. Jam secundum Primam Reg. ita procedimus.

Arcus major 44 gr. 12 pr.	Compl.	45 gr. 48 pr.
Arcus minor 13 gr. 33 pr.		13 gr. 13 pr.
		Aggreg 59 gr. 21 pr.	sinus 8,602,975
		Different. 32 gr. 15 pr.	sinus 5,336,145
			Differ. 3,266,820
			Semis 1,633,415 Quartus.
Rursum sunt, Term. proport.
βα 23 gr. 31 pr.
Si. t. 10,000,000		Si. R. 3,990,159		1,633,415

Concipiemus iterum, tertium esse Sinum rectum, cui ex Canone Sinuum competit arcus 99 gr. 24 pr.

Arcus major 23 gr. 31 pr.	Compl.	66 gr. 29 pr.
Arcus minor 9 gr. 24 pr.		9 gr. 24 pr.
	Summa	75 gr. 53 pr.	Sinus 9,698,011
	Differ.	57 gr. 5 pr.	Sinus 8,394,618
			Differ 1,303,393.
			Semis 651,697.	differe. Sinum

Versor. &c. cui addit a differentia alter a Sinuum versorum angulorum 13,791,570 producit Sinum versum 14,443,567 cujus arcus 116 gr. 23 pr. angulus αβγ, uti prius &c.

Exemplum. aliud in quo adhibentur Tangentes.

In triang. αβγ sphær. rectang. nota sunt basis αγ 239 gr. 56 pr. & angulus adjacens αγβ 71 gr. 15 pr. Inde per II. Prob. Sphær. innotescit etiam Crus βγ. Sunt enim per Primum ejus modum Term. prop.

αβγ 90 gr.	αγβ 71 gr. 15 pr.	Compl. 18 gr. 45 pr.	αγ 29 gr. 56 pr.
Si. t. 10,000,000 -	Si. 3,214,395		Tang. 5,757,998
Quartum 1,850,884 Tangent: Ejus arcus 10 gr,. 29 pr. Crus βγ.

Compendium Prosthaphæreticum ita habet.

Tertio, utpote Tangenti 5,757,998, debetur ex Canone Sinuum quasi sinui arcus 335 gr. 9 pr. Medius utpote sinus prabet arcum 18 gr. 45 pr.

Arcus major 35 gr. 9 pr.	Compl.	54 gr. 51 pr.
Arcus minor 18 gr. 45 pr.		18 gr. 45 pr.
	Aggreg.	73 gr. 36 pr.	Sinus	9,593,140
	Differ.	36 gr. 6 pr.	Sinus	5,891,964.
			Differ.	3,701,176.
			Semis	1,850,588.	Tangens quæsita
Cujus arcus 10 gr. 29 pr. Crus βγ idem, cum prius invento.

Exemplum tertium, in quo adhibetur Secans cum Tangente:

Eodem Problemate juxta modum ejus alterum sunt in Trianguli αβγ solutione ex isdem datis hi Term. prop.

αβγ	αγβ	71 gr. 15 pr.	αγ	29 gr. 56 pr.	Compl.	60 gr. 4 pr
Si. t. 10,000,000		Sec. 31,110,047			Tang.	17,367,146.
Quartus 54,029,273. Tang. Ejus arcus 79 gr. 31 pr. Comp. 10 gr. 29 pr. Crus βγ.

Per ϖροσϑαφαιρέσιν (prosthaphairesin) ita res procedit.

Quoniam secans 31,110,047, est major sinu toto Unica figura, ideo ab ea tollimus Unam ultimam figuram dextrorsum, ut remaneat sinus 3,111,004, cui ex Tab. competit arcus 18 gr. 7 pr. simili modo, quia Tangens extremo loco posita sinu toto major est una figura. Quare ultimo charactere ab ea demto, manet residuum 1,736,714, cui ex Canone Sinuum debetur arcus 10 gr. 0 pr.

Arcus major	18 gr. 7 pr.	Compl.	71 gr. 53 pr.
Arcus minor	10 gr. 0 pr.		10 gr. 0 pr.
		Aggr.	81 gr. 53 pr.	Sinus	9,899,827.
		Differ.	61 gr. 53 pr.	Sinus	8,819,898.
				Differ.	1,079,929
				Semis	539,964.

Huic numero additis duabus Siphris loca abjectarum ante duarum figurarum, Unius a Secante, alterius a Tengente, conflatur Tangens 53,996,400, cui ex Tab. Tangent. competit arcus 79 gr. 31 pr. Ejus Complemen. 10 gr. 29 pr. Crus quæsitum βγ, idem quod ante.

TERTIA REGULA.

Si in regula proport. se habuerit Sinus totus ad alium numerum Sinu toto minorem, quiquis ille sit, ut numerus Sinu toto major,quicunque & ille sic, ad alium; hoc pacto per ϖροσϑαφαιρέσιν (prosthaphairesin) operari poteris. Ex numero tertio, qui Sinu toto major est, servuntur ultimi septem characteres, septemSiphris intregri Sinus respondentes, reliquis, qui ad sinistram,.superfuerit, in minorem numerum, qui terminorum proporcionalium est medius, mulciplicatis, factoq; servato. Quod si unitas superfuerit, multiplicatione nulla opuserit. Deinde erit: Ut Sinus totus ad datum numerum minorem; ita residuæ illæ septem figuræ ad Quartum: hoc est,Minoris illius numeri,qui inReg. propor. medium locum tenet, ac Tertij in Tab. Sinuum arcus quærantur competentes, & cum his tanquam datis arcubus procedarur juxta PRIMAM Regulam. Invento Quarto numero addatur factus ex medio termino ante servatus, & Quartus ille numerus eric absolutus, cujus arcus juxta leges Trigonometricas investigetur.

Possunt nihilo minus termini in hanc Regulam cadentes per antecedentem etiam Regulam facilius supputari.

Exemplum. In præsenti Diagrammiate est illustris Stelæ in Cauda Ω Asccensio recta a Tropico ♋ numerata 82 gr. 31 pr. 34 sec. arcus æquinoct. σξ, & arcus αρ complementum maxima obliquitatis Eclipt. ad æquinoct. 60 gr. 28 pr. 30 sec. idlem cum arcu meridiani, quando Coluruis solstitiorum juxta primum Coeli motuum ad meridiem pertingit: Quæsitur arcus Eclipticæ: ω, exhibens punctum ω, quod cum stella proposita meridianum treansit. Sunt itaq. per Prius xxx Coronidis Triginometriæ nostræ, juxta Vulgarem operationem, Term. proport.

ασ 90 gr.	αβ 66 gr. 28 pr. 30 sec.	σξ 82 gr. 31 pr. 34 sec.
S. t. 10,000,000	-- Si. 9,168,859	-- Tang. 76,225,962.

Quartus 69,890,519. Tang. Ejus arcus 81 gr. 51 pr. 26 sec. ρω qui a O, ♋ ρ numeratus indicat 21 gr. 51 pr. 26 sec. ♏ cum dicta stella culminare.

Per Compendium Prosthaphæreticum ita proceditur.

A tertio termino, qui Sinu toto major est, initialis nimirum 7. sublata, relinquit 6,225,962, cui numero anquam Sinui arcus 38 gr. 20 pr. 2 sec. debetur. In medium auteem terminum 9,168,859, ducta 7 faciunt 64,182,013, servanda. Medius item terminaus, utpote Sinus, exhibet arcum 66 gr. 28 pr. 30 sec.

Arcus major	66 gr. 28 pr. 30	Compl.	23 gr. 31 pr. 30 sec.
Arcus minor	38 gr. 30 pr. 2		38 gr. 30 pr. 2
		Aggreg.	62 gr. 1 pr. 32	Sin.	8,832,000
		Differ.	14 gr. 58 pr. 32	Sin.	2,584,959
				Summa	11,416,959
				Semis	5,707,479

Huic numero additus factus ante servatus 64,182,013 componit Tangentem 69,890,492 cuius arcus 81 gr. 51 pr. 26 sec. plane idem qui ante.

Calculus ejusdem Exempli juxta præced. Secundam Reg.

A Tangente 76,225,962 remota finalis nota relinquit fictum Sinum 7,622,596, arcus 49 gr. 39 pr. 50 sec. Medij termini arcus habetur 66 gr. 28 pr. 30 sec.

Arcus major	66 gr. 28 pr. 30 sec	Compl.	23 gr. 31 pr. 30 sec
Arcus minor	49 gr. 39 pr. 50 sec		49 gr. 39 pr. 50 sec
		Aggreg.	73 gr. 11 pr. 20	Sin.	9,572,634
		Differ.	26 gr. 8 pr. 20	Sin.	4,405,486
				Aggreg.	13,978,120
				Semis	6,989,060

huic numero vice finalis characteris ante abjecti, addita Una Siphra componit Tangentem 69,890,600 cujus arcus 81 gr. 51 pr. 26 sec. Idem quiprius.

Et per hasce Regulas compendiosa per ϖροσϑαφαιρέσιν (prosthaphairesin) πραγματεία (pragmateia) ostensa est, si Sinus totus Terminorum proportionalium primus fuerit.

QUARTA REGULA.

Quando Sinu toto medium aut extremum Terminorum proportionalium locum obtinente, Primus numerus major est secundo vel Tertio, minor tamen Sinu toto, fiat: Ut Sinus totus ad secantem complementi illius arcus, qui majori numero in Tabula Sinuum tanquam sinus respondet; Ita minor numerus ad aliud: hoc est, duo arcus, qui illi Secanti in tabula Secantium, minori autem numero in Tabula Sinuum debetur, seponantur quasi dati, & cetera fiant, ut in Prima Regula dictum est: hoc tamen observato, ut, quia primo numero accessit siphra, aut forte plures, utis fieret Secans, Quarto procucto totidem pariter Siphræ adjiciantur.

Exemplum. Dantur r. ob. Trianguli γβα. Sphær. rectang. Crus αβ 28 gr. 12 pr. & angulus oppositus αγβ 36 gr. 0 pr.: ex quib. per IV. Prob. Sphær. Crus etiam reliquum γβ innotesit. Sunt enimper III. ejus modum.

Term. proport. juxta Vulgar operat.

αγβ 36 gr. 0.		αβγ 90 gr.		αβ 28 gr. 12 pr.
Tang. 7,265,424		S. t. 10,000,000		Tang. 5,361,954.
Quartus 7,380,098. Sinus: Ejus arcus 47 gr. 33 pr. 44 sec. Crus γβ.

Compendium Prosthaphæreticum ita habet.

Terminorum translatio sic fiat, ut primo loco ponatur Sinus totus, altero Tangens major per additam unam siphram aucta, instar Secantis, 72,654,240 tertio Tangens minor, qua in Sinum transmutata concipiatur. Jam Secanti 72,654,240 respondet arcus in Tabl Secantium 82 gr. 5 pr. 30 sec. Cujus sumitur complement. 7 gr. 54 pr. 30 sec. Tangenti in Sinum transfigurata 5,361,954, debetur ex Canonoe Sinuum arcus 32 gr. 25 pr. 30 sec. Habemus jam duos arcus Primæ Regulæ adaptos.

Arcus major	32 gr. 25 pr. 30 sec.	Compl.	57 gr. 34 pr. 30 sec.
Arcus minor	7 gr. 54 pr. 40 sec.		7 gr. 54 pr. 40 sec.
		Aggreg.	65 gr. 29 pr. 10 sec.	Sinus	9,098,607.
		Differ.	49 gr. 39 pr. 50 sec.	Sinus	7,622,605.
				Differ.	1,476,002
				Semis	738,001

huic Semissi annexa Una Siphra ad finem, propterea quod Tangenti primo loco posita adjecta etiam fuit Una Siphra, ut fieret ea Secans, efficit Sinum 7,380,010 cujus arcus 47 gr. 33 pr. 41 sec. est crus γβ idem cum ante invento.

QUINTA REGULA.

Quando primus numerus minor est Secundo vel Tertio, & minor Sinu toto, tunc si major quidem numerorum fuerit minor Sinu toto, fiat, Ut Sinus totus ad Secantem complementius arcus ,qui minori numero tanquam Sinui in Tabula Sinuum respondet: Ita major numerous ad aliud: hoc est: duo arcus, tum qui illi Secanti, tum qui majori numero in Sinuum Canone respondent, seponantur, ut dati, & cetera fiant pro re nata secundum ea, quæ antea in Prima aut Secunda Reg. sunt proposita.

Si vero Primus terminus minor fuerit; major autem numerus major Sinu toto, detrahatur ex eo minor aliquoties, donec numeru sreliquus Sinu toto minor sit: Vel, subtrahatur Sinus totus, quoties fieri porest: fiatq; rursum: Ut Sinus totus ad Secantem complementi illius arcus, qui datorum numerorum minori tanquam Sinui respondet; ita reliquus numerus majoris ad aliud, uti dictum est, inventoq; numero Quarto adjiciatur Sinus integer totis, quoties minor numerus ex majore ablatus est, ut totus quartus numerus quæsitus conficiatur.

Sin deniq; tam primus terminorum quam extremus totum Sinum excesserint, primus autem tertio minor, Primi quasi Secantis (nisi fuerit Secans) quæratur arcus & hujus complementum. Deinde tertio numero auferatur finalis nota aut Una, aut plures, donec remaneat Sinus, cujus quæratur arcus: ↦ cum inventis binis arcubus juxta Primam regulam procedatur. Invento autem numero adjiciantur loco abjectæ antea Unius aut plurium figurarum tot Siphræ, ut legitimus numerus Quartus proveniat.

Exemplum Primi Casus: Dantur Triang. αβγ. Sphær. rectang, basis γα 84 gr. 50 pr. & Crus γβ 84 gr. 22 pr. datur itaq. angulus etiam βγα per XIV. Prob. Sphær. Nam per IV. ejus modum sunt Term. proport.

γα 84 gr. 50 pr.	Compl.	50 gr. 10 pr.	γβα	90 gr.	βα 84 gr. 22 pr.	Compl.	5 gr. 38 pr.
Tang. 904,204				S. t. 10,000,000		Tang. 986,383.
Quartus 10,908,855, Secans: Ejus arcus 23 gr. 33 pr. 13 sec. angulus βγα.

Compendium ϖροσϑαφαιρέσιως (prosthaphairesios) tale est.

Primus terminorum duabus Sipheris auctus producit Secantem 90,420,400, cujus arcus 83 gr. 39 pr. 1 sec. Compl. 6 gr. 22 pr. 59 sec. Tertio numero 986,383, tanquam Sinui respondet arcus 5 gr. 39 pr. 39 sec.

Arcus major	6 gr. 22 pr. 59 sec.	Compl.	83 gr. 39 pr. 1 sec.
Arcus minor	5 gr. 39 pr. 69 sec.		5 gr. 39 pr. 69 sec.
		Aggreg.	89 gr. 18 pr. 40 sec.	Sinus	9,999,277
		Differ.	77 gr. 59 pr. 22 sec.	Sinus	9,781,093.
				Different.	218,184
				Semis	109,092.

cui numero adjectæ dua Siphra, quæ primo etiam termino accessere, constituunt Secantem 10,909,200 cujus arcus 23 gr. 33 pr. 28 sec. angulus .γα quadrante saltem Unius minuti ab ante invento differens.

Exemplum Secundi casus, in quo primus numerus minor est; Sinu toto, Ultimus vero Sinu toto major.

dantur Trianguli αβγ Sphær. rectang. Crura duo, γβ 80 gr. 38 pr. & αβ 61 gr. 46 pr. Quaritur angulus αγβ per XVI. Prob. Sphær. Nam juxta modum ejus III. sunt Term. proport.

γβ	80 gr. 38 pr.	αβγ	90 gr.	αβ	61 gr. 46 pr.
Sin.	9,866,671	S. t.	10,000,000	Tang.	18,623,894
Quartus 18,875,560. Tangens: Ejus arcus 62 gr. 1 pr. 10 sec. angulus βαγ.

Compendium ϖροσϑαφαιρέσιως (prosthaphairesios) tale est.

Primus termin. Una Siphera auctus suppeditat Secantem 98,666,710 cujus arcus 84 gr. 11 pr. Complem. 5 gr. 49 pr. Ab ultimo 18,623,894 sublatus terminus primus 9,866,671 semel, relinquit 8,757,223, cujus resisui arcus ex Tabula Sinuum est 61 gr. 7 pr. 50 secun.

Arcus major	61 gr. 7 pr. 50 sec.	Compl.	28 gr. 52 pr. 10 sec.
Arcus minor	5 gr. 49 pr. 0 sec.		5 gr. 49 pr. 0 sec.
		Aggreg.	34 gr. 41 pr. 10	Sinus	5,690,802
		Differ.	23 gr. 3 pr. 10	Sinus	3,915,788
				Different.	1,775,014
				Semis	887,507

Huic numero additus integer Sinus semel, propterea quod minor numerus semel a majori fuerat sublatus, componit 1,887,507, cui rursum ad finem apposita Siphra, qua eadem prim 1uoq. termino, utis Secans fieret, accessit, componit Tangentem 18,875,070, cuius arcus 65 gr. 5 pr. 10 sec. angulus βαγ idem qui prius.

Exemplum Tertij Casus, in quo primus terminus est minor tertio, Uterque vero Sinu toto major.

In triang. αβγ Sphær. rectang. dantur, basis αγ 30 gr. 8 pr. 55 sec. & Crus βγ 111 gr. 33 pr. 52 sec. Quæsitur angulus βαγ per XV. Prob. Sphær. Sunt enim per V. eijus modum Term proport.

αγ	30 gr. 8 pr. 55 sec.	αβγ	90 gr.	βγ	11 gr. 33 pr. 52 sec.
Comp.	59 gr. 51 pr. 5 sec.			Comp.	78 gr. 26 pr. 8 sec.
Secant.	19,910,618	S. t.	10,000,000	Sec.	49,882,776.

Quartus 25,053,354. Secans: Ejus arcus 66 gr. 28 pr. 30 sec. Compl. 23 gr. 31 pr. 30 sec. angulus βαγ.

Calculus Prosthaphæreticus talis est.

Primus Terminus utpote Secans habet arcum 59 gr. 51 pr. 5 sec. Copml. 30 gr. 8 pr. 55 sec. Ultimus finali decurtatum est 4,988,277: hujus arcus ex Canone Sinuum 29 gr. 55 pr. 21 sec.

Arcus major	30 gr. 8 pr. 55 sec.	Compl.	59 gr. 51 pr. 5 sec.
Arcus minor	29 gr. 55 pr. 21 sec.		29 gr. 55 pr. 21 sec.
		Aggreg.	89 gr. 46 pr. 26 sec.	Sinus	9,999,921
		Differ.	29 gr. 55 pr. 44 sec.	Sinus	4,989,248
				Differ.	5,010,673
				Semis	2,505,337

Huic apposita siphra ab finalem tertio ademtam, conflatur Secans, 25,053,370: Cujus arcus 66 gr. 28 pr. 30 sec. Compl. 23 gr. 31 pr. 30 sec. ang. βαγ idem qui ante.

SEXTA REGULA.

Si primus terminorum proport. tertio major minorve, uerit quoq; major toto Sinu, atq; idem etiam Secans, ejus arcus utpote dati complementum erit unus arcuum ad xxx requisitorum. Si vero primus non fuerit Secans,sed alius quidam, ejus tanquam Secantis, quæratur arcus ex canone Secantium,cujus complementum dabit in proportione ϖροσϑαφαιρέσιν (prosthaphairesin) medium terminum loco Sinus integri in primum locum jam transferendi, ultimo assignato illi, qui in Vulgari operatione ultimus erat, cujus tanquam Sinus (modo Sinum totum non excesserit) arcus, erit alter ille juxta Primam Regulam cum prius invento arcu usurpandus.

Sin extremus Terminorum Sinu integro itidem major fuerit, quæratur primum Sinus complementi, quod Secanti respondebat: deinde extremus Terminus per Sinum totum devidatur, Quotus autem emergens in Sinum modo inventum multiplicetur, facto servato. Residui autem numeri tanquam Sinus ex Canone Sinuum quæratur arcus, isq; unum arcum in ϖροσϑαφαιρέσιως (prosthaphairesios) negocio exhibebit,alterum complemento Seantis præbente. Peracta juxta Primam Regulam operatione, numero producto addatur factus ante servatus & aggregatum suppedicabit Quartum Terminum quæsitum.

Si deniq; terminorum tertius Sinu toto major hac ratione fuerit, ut abjectus ex eo Sinus totus non relinquat numerum, qui convenienter in Canonem Sinuum immitti, ejusq; arcus excerpiqueat, tollatur ab eo finalis nota, & residui ex Tabula Sinuum arcus quæratur, ac porro cum arcubus procedatur, uti oportet.

Exemplum primi Casus, in quo tertius Sinu toto minor est.

Trianguli αβγ Sphær. rectang. Crus γβ 36 gr. 19 pr. & angulus adjacens αγβ 23 gr. 31 pr. patefaciunt per XII. Prob. Sphær. angulum reliquum γαβ. Nam per III. ejus modum sunt juxta Vulgarem operat. Termin proport.

αβ	36 gr. 19 pr.	αβγ	90 gr.	βαγ	23 gr. 31 pr.
Sec.	12,410,705	S. t.	10,000,000	Si.	3,990,159

Quartus 3,215,095 Sinus: Ejus arcus 18 gr. 45 pr. 15 sec. Compl. 71 gr. 14 pr. 45 sec. ang. γαβ.

Compendium Prosthaphæreticum ita habet.

Secantis arcus 36 gr. 19 pr. Compl. 53 gr. 41 pr. Unus arcuum: alter datur.

Arcus major	53 gr. 41 pr.	Compl.	36 gr. 19 pr.
Arcus minor	23 gr. 31 pr.		23 gr. 31 pr.
		Aggreg.	59 gr. 50 pr.	Sinus	8,645,673
		Differ.	12 gr. 48 pr.	Sinus	2,215,485
				Differ.	6,430,188
				Semis.	3,215,094

Exemplum Secundi casus, in quo Tertius, itidem com primo, Sinu toto major est.

datur Triang. αβγ Sph. rectang. angulus Uterq; obliquus, αγβ 23 gr. 31 pr. & βαγ 66 gr. 38 pr. Quaritur basis αγ per X. Prob. Sphær. Nam per modum ejus III. sunt juxta Vulg. πραξιν (praxin) Ter prop.

βαγ	66 gr. 38 pr.	αβγ	90 gr.	βγα	23 gr. 31 pr.
				Compl.	66 gr. 29 pr
Tang.	23,145,565	S. t.	10,000,000	Tang.	22,980,141
Quartus 9,928,529. Sinus: Cujus arcus 83 gr. 8 pr. 45 sec. Compl. 6 gr. 51 pr. 15 sec. Bas. αγ

προσϑαφαιρέσις (prosthaphairesis) ita procedit.

Primi numeri tanquam Secantis arcus est 64 gr. 24 pr. 52 sec. Compl. 25 gr. 35 pr. 52 sec. Tertius per Sinum totum, qui medius est Terminorum, divisus, producit in Quoto 2, residuis manentib. 2,980,141, cui numero tanquam Sinui respondet arcus 17 gr. 20 pr. 18 sec. Complemento autem Secantis 25 gr. 35 pr. 52 sec. ex Tabula Sinuum excerptus respndet Sinus 4,320,507, qui multiplicatus per Quotum 2, facit 8,641,014 servanda.

Arcus major	25 gr. 35 pr. 52 sec.	Compl.	64 gr. 24 pr. 8 sec.
Arcus minor	17 gr. 20 pr. 18 sec.		17 gr. 20 pr. 18 sec.
		Aggreg.	81 gr. 44 pr. 26 sec.	Sinus	9,896,276
		Differ.	47 gr. 3 pr. 50 sec.	Sinus	7,321,137
				Differ	2,575,139
				Semis	1,287,569

Huic Semissi additus factus ante servatus 8,641,014, componit Sinum 9,928,583, cujus arcus 83 gr. 8 pr. 54 sec. Compl. 6 gr. 51 pr. 6 sec. Basis αγ a prius inventa saltem 9 sec. deficiens.

Exemplum Tertij Casus.

Trianguli αβγ Sph. rect. dantur Crus &947;β 11 gr. 33 pr. 52 sec. & basis γ͍ 30 gr. 8 pr. 55 sec. Quaritur Crus reliquum αβ per III. Prob. Sphær. Nam per Ult. ejus modum sunt juxta Vulgar. operat. Term. proport.

γα	30 gr. 8 pr. 55 sec.	γβα	90 gr.	γβ	11 gr. 33 pr. 52 sec.
Sec.	11,564,362	S. t.	10,000,000	Sec.	10,207,383
Quartus 8,826,585, Sinus: Ejus arcus 28 gr. 2 pr. 13 sec. Crus βα

Calculus Prosthaphæreticus ita perficitur.

Notandum hic; quod onmia Exempla, quæ in alterum hujus Regulæ membrum cadunt per Tertiæ præceptum pari dexteritate, minori opera supputari possunt.

SEPTIMA REGULA.

Si deniq; contigerit, ut nullus termin. proportionalium sit Sinus totus, duplici xxx labore opus erit, ut nimirum juxta ea, quæ in proxime præcedentibus tribus Regulis fuerunt exposita, primum Termin. efficias secantem cujus arcus complementum,aruum ad ϖροσϑαφαιρέσιως (prosthaphairesios) pertinentium Unus erit; alterum suppeditabit ex Canone Sinuum Terminus tertius, ad formam Sinus, si eam non habuerit, redactus: Et sic juxta Regularum trium priorum aliquam exihibit numerus, cujus tanquam Sinus quæratur conveniens arcus, isq; in altera ϖροσϑαφαιρέσει (prosthaphairesei) arcuum Unus erit, reliquum subministrante itidem ex Tabula Sinuum termino medio primitus dato, Sinus speciem, si eam non habuerit, induente: & sic quoq; stabunt ad hanc alteram ϖροσϑαφαιρέσιν (prosthaphairesin) requisita. Producto adnectantur tot Siphræ, tum quod ad formandam Secantem primi termini ante fuerunt adhibitæ, tum quot figuræ a fine tertij medijq; terminorum primum datorum fuerant abjectæ, ut sinus forma relinquereretur. Hujus ultima Regulæ Usus tam Patet, ut non ad Sphærica solum Triangula, sed plana etiam sese extendat, quando nimirum ex datis lateribus angulum datum comprehendentibus anguli reliqui juxta præscriptum DECIMI SEXT Prob. sunt determinandi.

Exemplum ex classe Triangulorum planorum desumtum.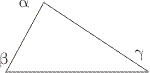

In Triang. βαγ plano obliquangulo vario dantur Latera duo, βγ 980,635, αγ 193,490, & angulus per ista comprehensus αγβ 222 gr. 47 pr. 58 sec: ex quibus per XVI. Prob. Plan. invenitur angulus αβγ Vulgaris operatione per hosce Term. proport.

587,063		393,572		Tang.	49,595,714
Quartus 33,249,386. Tang. Cujus arcus 73 gr. 15 pr. 39 sec.

Prior ϖροσϑαφαιρέσις (prosthaphairesis) ita perficitur.

Primo terminorum 587,063 addita dua Siphra effeciunt Secantem 58,706,300, eijus arcus 80 gr. 11 pr. 33 sec. Compl. 9 gr. 48 pr. 27 sec. arcus quæsitorum Unus. A tertio termino, qui Sinu tot major est, 49,494,714 dextrosum ablata una figura, relinquit Sinum 4,959,517, cujus arcus 29 gr. 42 pr. 58 sec. ad ϖροσϑαφαιρέσιν (prosthaphairesin) perinentium alter.

Arcus major	29 gr. 53 pr. 58 sec.	Comp.	60 gr. 16 pr. 2 sec.
Arcus minor	9 gr. 48 pr. 27 sec.		9 gr. 48 pr. 27 sec.
		Aggreg.	70 gr. 4 pr. 29 sec	Sinus	9,401,378
		Differ.	50 gr. 27 pr. 35 sec	Sinus	7,711,772
				Differ.	1,689,606
				Semis	844,803

hujus tanquam Sinus arcus est 4 gr. 50 pr. 46 sec. arcuum Unus ad alteram ϖροσϑαφαιρέσιν (prosthaphairesin) requisitus. Terminorum autem primitus datorum medio 393,572 tanquanm Sinui, competit arcus 2 gr. 15 pr. 20 sec.

Jam altera ϖροσϑαφαιρέσισ (prosthaphairesis) ita peragitur.

huic adfigenda sunt tres Siphra, dua quidem ob totidem primo termino, ut is fieret Secand, additus; & Una propter figuram tertio termino addendam, ut is fieret Sinus; & emergit quasitus numerus 33,249,000 Tangens, cujus arcus 73 gr. 15 pr. 39 sec. idem cum eo, quem Vulgaris operatio producebat.

Exemplum aliud ex Sphæricis petitum.

In Triang. αβγ Sphær. rectang. dantur, basis αγ 30 gr. 8 pr. 55 sec. & crus αβ 11 gr. 33 pr. 52 sec. Quæritur angulus αγβ per XV. Prob. Sphær. nam per X. ejus modum sunt juxta consvetam operationem Term. prop.

αγ	30 gr. 8 pr. 55 sec.	αγ	30 gr. 8 pr. 55 sec.	βγ	11 gr. 33 pr. 52 sec.
Compl.	59 gr. 51 pr. 5 sec.	Compl.	59 gr. 51 pr. 5 sec.	Compl.	78 gr. 26 pr. 8 sec.
Tangens	17,217,222	Sinus	8,647,256	Secans	49,882,776
Quartum 25,053,352. Secans: Ejus arcus 66 gr. 28 pr. 20 sec.. Comp. 23 gr. 31 pr. 30 sec. angulus βαγ.

Compendium ϖροσϑαφαιρέσιντικὀν (prosthaphairetikon) ita habet.

Primo termin. 17,217,222 in Tab. Secantium immisso respondet arcus 54 gr. 29 pr. 32 sec. Comp. 35 gr. 30 pr. 28 sec. Ultimo finali Charactere imminuto 4,988,277 cers Sinui debetur arcus 29 gr. 55 pr. 21 sec.

Arcus major	35 gr. 30 pr. 28 sec.	Compl.	54 gr. 29 pr. 32 sec.
Arcus minor	29 gr. 55 pr. 22 sec.		29 gr. 55 pr. 22 sec.
		Aggreg.	84 gr. 24 pr. 53 sec.	Sin.	9,952,524
		Differ.	24 gr. 34 pr. 11 sec.	Sin.	4,158,002
				Differ.	5,794,522
				Semis	2,897,261

Ejus arcus ex Canone Sinuum petitus 16 gr. 50 pr. 30 sec. Medius Term. utpote Sinus exhibet arcus 59 gr. 51 pr. 5 sec.

Arcus major	59 gr. 51 pr. 5 sec.	Compl.	30 gr. 8 pr. 55 sec.
Arcus minor	16 gr. 50 pr. 30 sec.		16 gr. 50 pr. 30 sec.
		Aggreg.	46 gr. 59 pr. 25 sec.	Sinus	7,312,379
		Differ.	13 gr. 18 pr. 25 sec.	Sinus	2,302,677
				Differ.	5,010,702
				Semis	2,505,351

Huic numero adnexa Una Siphra, ob eam, quæ Tertio termino ablata fuit, componit Secantem 25,053,510: Ejus arcus 66 gr. 28 pr. 30 sec. Compl. 23 gr. 31 pr. 30 sec. angulus βαγ, idem cum Vulgariter quæsito.

Et hactenus doctrina ϖροσϑαφαιρέσεων (prosthaphaireseon) Trigonometricaru sit exposita: de quibus tamen minus in pulvere hoc versacos serio monco, parce provideq; ijs ututantur compendijs, præsertim ubi vel primus Terminorum, vel reliqui in Universum Sinus integri nulli fuerint, cum & magnam ista curam ac circumspectionem, & frequentem ad Tabulas Sinuum ac Secantium recursum, paremq; fere in maxima exemplorum turba temporis ac laboris impensam cum Usitata suppurandi forma requirant: nisi forte examinis aut voluptatis gracia hujus modi exercitiorum variationes instituere voluerint: Siquidem prosperato temporis operæq; compendio utriusq; dispendium, ob hallucinationis facilitatem hauc raro experientur; inprimis quando animus non fuerit serenus ac præsens, sed in diversa ob curarum aliaru nubila ac ventos distractus. Potius itaq; tum aut Vulgarem operandi modum evidenti faciliq; demonstrationi innitentem sequamur; aut quæ eundem ad scopum, pari semitæ rectitudine, admiranda calculi facilitate deducunt, Logarithmorum compendia,vera temporis ac laborum compendia, amplectamur.

Ut jam integra, de triangulis a nobis instituta tractatio, Lectori uno in conspectus sit, sequentibus duabus Tabellis eam exhibemus.

Die Quelle ist als PDF-Datei bei der Elektronischen Bibliothek Schweiz hinterlegt.