Lehrsätze im rechtwinkligen Dreieck
Im rechtwinkligen Dreieck gibt es drei für die Navigation wichtige Sätze über die Verhältnisse der Seiten. Sie sind deshalb wichtig. Weil man durch das Fällen einer Höhe jedes beliebige Dreieck in zwei rechtwinklige teilen kann. Die Höhe ist eine Strecke, die auf einer Seite senkrecht steht und durch die gegenüberliegende Ecke geht.
Der Satz des Pythagoras
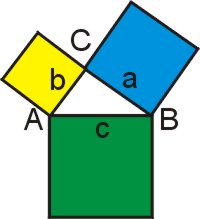Der Satz des Pythagoras besagt, dass in einem rechtwinkligen Dreick die Summe der Quadrate der Kathetenlängen gleich der Summe des Quadrats der Hypotenusenlänge ist.
a2 + b2 = c2
Dieser Satz gibt den Einstieg in die Berechnung von beliebigen Dreiecken, wenn man die Länge zweier Seiten kennt. Mit dem Rechenschieber lassen sich diese Art Aufgaben schnell lösen.
Der Satz des Thales
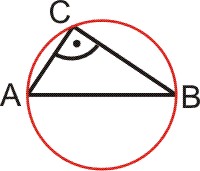Ist AB der Durchmesser eines Kreises, so ist jedes Dreieck, dessen dritte Ecke auf dem Kreis liegt rechtwinklig.
Der Satz des Euklid
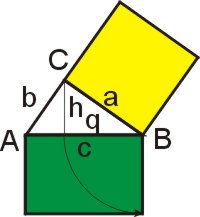Euklid setzte die Hypotenuse des rechtwinkligen Dreiecks ins Verhältnis zur Kathete und dem Hypotenusenabschnitt, den die Höhe auf die Hypotenuse erzeugt. Das Quadrat der Kathete ist gleich dem Produkt aus Hypotenusenlänge und Länge des Hypotenusenabschnitts unter der Kathete.
- a2 = c · q
Der Höhensatz im rechtwinkligen Dreieck
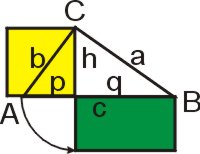Dieser Satz im Zusammenhang mit dem Satz von Euklid ist wichtig, denn er gibt den Einstieg in die Sätze über Winkel im schiefwinkligen Dreieck.
Das Quadrat der Länge der Höhe h auf die Hypotenuse ist gleich dem Prokukt der beiden durch die Höhe erzeugten Hypotenusenabschnitten p und q.
- h2 = p · q
Der Höhensatz ist eine Sonderform des Sehnensatzes. Der Kreis über AB als Durchmesser ist ein Thales-Kreis!
Der Höhensatz im allgemeinen Dreieck (Projektionssatz)
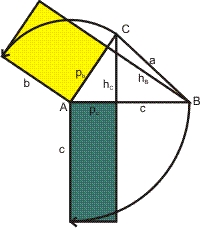In einem beliebigen Dreieck sind die Rechtecke, die aus einer Seite und der orthogonalen Projektion der anderen gebildet werden, flächengleich.
- c · pc = b · pb
Den Höhensatz kann man im allgemeinen, schiefwinkligen Dreieck formulieren. Er ist die Verallgemeinerung des Satzes des Euklids für das rechtwinklige Dreieck. (Systematisch passt er daher zu den hier aufgeführten Sätzen.)
Eine andere Formulierung:
- c = pc + qc = a · cos β + b · cos α
