Die Deklination der Sonne

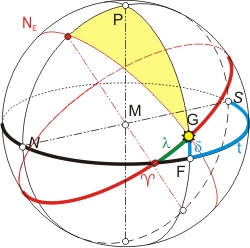Skizze Zur Berechnung der Deklination δ der Sonne muß ein weiteres Koordinatensystem eingeführt werden: das Ekliptikale System. Die Ekliptik ist die Ebene, auf der die Planeten auf Ellipsen um die Sonne kreisen. Die Ebene ist gegenüber dem Himmelsäquator um ε = 23° 27′ geneigt. Ihre Achse durchstößt die Himmelskugel im ekliptikalen Nordpol NE. (Der Himmelsäquator fällt ja mit dem der Erde zusammen, ebenso die Erdachse mit der Weltachse, die die Himmelskugel im (Nord-)Pol P durch­stößt.) Da auch die Mittelpunkte des Äqua­tor­sys­tems und des Ekliptiksystems zusammen fallen, schnei­den sich die beiden Ebenen (die Schnitt­linie geht durch den gemeinsamen Mittelpunkt M). Und da die Kugel ja den "Einheitsradius 1" hat, gibt es zwei Schnittpunkte der Schnittlinie mit der Himmelskugel: den Früh­lings­punkt ♈ und den Herbstpunkt ♎. Vereinbarungsgemäß zählt man den Winkel auf der Ekliptik von Früh­lings­punkt aus entgegen dem Uhrzeigersinn.

Da sich die Sonne ☉ in der Ebene der Ekliptik bewegt, braucht es nur eine Koordinate: die ekliptische Länge λ. Und die ist die Hypotenuse im Dreieck ♈FG, in dem auch der Winkel G♈F = ε bekannt, gesucht ist die Seite FG = δ. Wir können also die Nepersche Regel anwenden: F♈* ∠♈ λ ∠G δ* ergibt: cos δ* = sin ε · sin λ = sin δ.

Oben wurde erwähnt, dass sich die Deklination der Sonne täglich ändert. Das wird an der Abbildung verständlich. Am Frühlingspunkt ♈ ist δ = 0 und die Mittagshöhe der Sonne h☉ = ε und der Tag hat 12 Stunden. (Ist leicht mit den oben abgeleiteten Formeln für δ = 0 zu berechnen.) Nun werden die Tage länger, bis die Sonne den oberen Punkt ihrer Bahn erreicht hat; δ = ε. Dieser Punkt liegt 90° vom ♈-Punkt entfernt. Da die Sonne den ♈-Punkt nach einem vollen Umlauf von 360° wieder erreicht und dabei ein Jahr (zu 365,25 Tagen) vergangen ist, ist das ¼ Jahr nach dem Frühlingspunktdurchgang. Es entspricht also ein Tag einem Fortschreiten der Sonne auf ihrer ekliptischen Bahn um 1,015° Mit diesem Wert kann man die Deklination δ für jedes Datum berechnen, wenn man weiss, wann der Durchgang durch den Frühlingspunkt war.

Leider ist die Wirklichkeit nicht so ideal. Man muss den ♈-Punkt jährlich bestimmen. Im Jahr 2014 war der Zeitpunkt am 20. März um 17:57 h MEZ. Die Gründe werden auf Astronomie-Sites ausführlich erklärt.

Kann man herausfinden, auf welcher Insel im Ozean man gestrandet ist, wenn man nur einen Rechenschieber dabei hat und das Datum weiss? Mit diesen Formeln und der Messung der Schattenlänge zu Mittag kann man!
Valid HTML 4.01 © Rainer Stumpe URL: http://www.rainerstumpe.de