Konstruktive Lösung der Aufgaben im sphärischen Dreieck

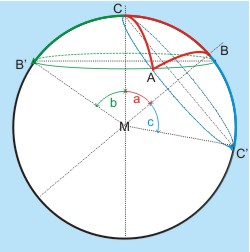Die Aufgaben im sphärischen Pol-Dreieck ABC kann man grafisch durch Konstruktion der senkrechten Paral­lelprojektion der Kugel und des sphärischen Dreiecks in die Ebene lösen. Dazu legt man die Ebene (blau), in die die Punkte auf der Kugel projiziert werden sollen, durch den Mittelpunkt M der Kugel und durch zwei Punkte B, C des sphä­rischen Dreiecks (die ja auf einem Groß­kreis liegen). Durch den Punkt A des sphä­rischen Drei­ecks legt man zwei Kleinkreise ABB′ und ACC′, die je­weils die Verbindungslinie des Kugelmittelpunktes M mit einer der beiden anderen Ecken als Achse haben. Wegen der Kugelsymmetrie bleiben die Groß­kreis­bo­gen­längen AB und AC gleich, wenn man um die Ach­sen MB bzw. MC "dreht". Man kann also die Groß­kreis­bögen in die Projektionsebene drehen. Das sphä­rische Dreieck ABC ist nun unter Beibehaltung der Sei­ten­län­gen "eingegebnet". Auch die sphärischen Winkel des Poldreiecks kann man in die Ebene projizieren.

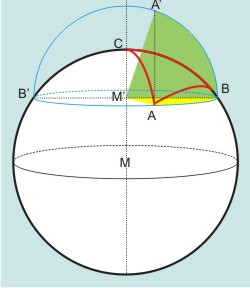Dazu dreht man den Kleinkreis ABB′ durch A um seine Achse BB′ in die blaue Ebene. Dabei bleibt der Winkel ∠AMB erhalten und kann in der Ebene als Winkel ∠A′MB abgelesen werden.
Praktisch schlägt man einen Kreis mit dem Durch­mes­ser BB′ um den Mittelpunkt M′ des Kleinkreises, er­rich­tet dann auf BB′ das Lot durch A und findet im Schnitt­punkt des Lots mit dem Projektionskreis A′.
Der Winkel γ = ∠AM′B (gelb) ist gleich dem Winkel γ = ∠A′M′B (grün), den man in der Projektionsebene leicht ablesen kann. In der Navigation entspräche dieser Winkel der geografischen Länge, mit B als Mittagspunkt.

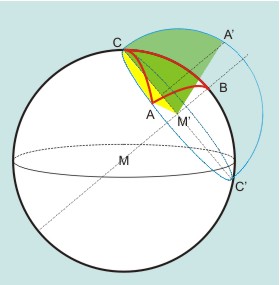In analoger Weise erhält man den ∠AMC = β durch Umklappen des Kleinkreises CAC′ durch A, dessen Achse durch B geht: β = CMA′.

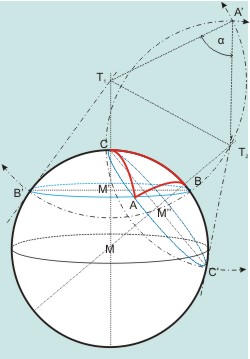Etwas aufwändiger ist die Projektion des Winkels α = ∠CAB zu konstruieren. Er wird durch die beiden Tangenten an die Großkreise AC und AB in A ein­ge­schlos­sen. Diese beiden Tangenten AT₁ und AT₂ schneiden die Achsen der Kleinkreise ABB′ und ABB′ in den Punkten T₁ bzw. T₂. Man dreht sie um die Achsen MC bzw. MB in die Projektionsebene: AT₁ ⇒ B′T₁ und AT₂ ⇒ C′T₂. Damit erhält man die Punkte T₁ und T₂ durch die Tangente an den Großkreis in den Punkten B′ und C′. Das Dreieck AT₁T₂ wird nun in die Pro­jek­tions­ebene gedreht, indem man um T₁, T₂ die Kreise mit den Radien AT₁ = B′T₁ bzw. AT₂ = C′T₂ schlägt. Am Schnitt­punkt A′ in der Projektionsebene wird der Winkel α gefunden.

Konstruktionsbeispiel

Gegeben sind die Seiten a = 60,4° und b = 54,4° und der Winkel γ = 51° eines sphärischen Dreiecks. 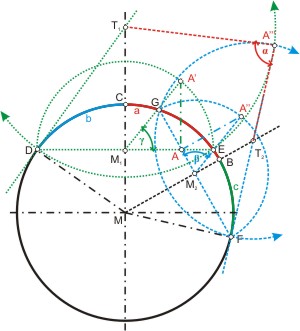Als erstes zeichnet man einen (Rand-)Kreis, mar­kiert dessen Mittelpunkt M und zieht das Ach­sen­kreuz durch den Mittelpunkt. Auf dem Rand­kreis trägt man die Kreissegmente a und b ab, die der Länge (d. i. dem Winkel am Mit­tel­punkt M) der gegebenen Dreiecksseiten entsprechen. Die Spur des Kleinkreises durch die Ecke A des Dreiecks parallel zur x-Achse schneidet den Kreis in einer der Drei­ecks­seiten (hier D). Die Projektion des Mit­tel­punk­tes M₁ findet man als Schnittpunkt mit der Achse des Kreises. Über der Spur des Klein­kreises mit dem Mittelpunkt M₁ zeichnet man den Thales-Kreis. Am Mittelpunkt M₁ trägt man den gegebenen Winkel γ an, und ver­län­gert den Schenkel bis zum Schnittpunkt A′ mit dem Thales-Kreis. Von A′ fällt man das Lot suf die Spur des Kleinkreises und erhält die Projektion der dritten Drei­ecks­ecke A auf die Zeichenebene.
Nun verbindet man den Mittelpunkt des Krei­ses mit der zweiten gegebenen Ecke des sphärischen Dreiecks (hier B) und verschiebt das Lot auf diese Strecke bis es A und den Kreis in F und G schneidet. Die Strecke zwi­schen den Kreisschnittpunkten ist die Spur des zweiten Kleinkreises mit dem Mittelpunkt M₂, über der man einen Thales-Kreis mit M₂ als Mittelpunkt errichtet. In A errichtet man ein zweites Lot auf diesen Kleinkreis, und verbindet dessen Schnittpunkt A″ mit dem Thales-Kreis mit dem Mittelpunkt des Kleinkreises. Hier liest man den gesuchten Winkel β = 68,1° ab. Gleichzeitig hat man die Länge der dritten Seite c = 42,2° des sphärischen Dreiecks gefunden: es ist der Kreisbogen zwischen B und dem Be­rüh­rungs­punkt F des zweiten Kleinkreises mit dem Kreis.
Die beiden Tangenten an die beiden Kleinkreise, die den Winkel α einschließen, konstruiert man als Senk­rechte zum Kreisradius in den Ecken des sphärischen Dreiecks D und F. Ihre Schnittpunkte T₁ und T₂ mit den Achsen der Kleinkreise sind die Mittelpunkte zweier Kreise, deren Schnittpunkt A′″ die Projektion der Dreiecksecke A ist. Der Winkel zwichen den Ver­bin­dungs­gera­den ist der gesuchte Winkel α = 84,6°.

Das Ergebnis hängt überwiegend von der Zeichengenauigkeit ab — wie man durch Nachrechnen dieser III. Hauptaufgabe im schiefwinkligen sphärischen Dreieck leicht feststellen kann, ist es nicht bahnbrechend.

• Zum Thema gehörende Seiten:
• [sphärische Trigonometrie - Grundlagen]
• [Das rechtwinklige sphärische Dreieck]
• [Das schiefwinklige sphärische Dreieck]
• [Anwendungen der sphärische Trigonometrie] (Orthodrome, Tageslänge, Deklination der Sonne)
• [Anwendungen der sphärische Trigonometrie] (Sonnenhöhe, indischer Kreis)
• [Die Nepersche Regel]
• [Beispielrechnung]
• [Konstruktion mit Projektion der Kugel]