Sphärische Trigonometrie

Das schiefwinklige sphärische Dreieck

Das schiefwinklige sphärische Dreieck, in dem kein Winkel größer ist als 180° (Eulersches Dreieck), wird von Navigatoren gerne vermieden, denn die Formeln verursachen einen größeren Rechenaufwand als das rechtwinklige. (In der Astronavigation ist das leider nicht zu vermeiden, denn die grafische Lösung der Auf­gaben durch Konstruktion der Projektion in die Ebene ist nicht genau genug.) Auch gibt es — bis auf den Sei­ten­sinus­satz im schiefwinkligen sphärischen Dreieck — keinen einfachen Merk­satz. Wir wollen aber den For­mel­satz ableiten, vielleicht hilft es ja beim Erinnern — außerdem ist es nicht so schwer, denn die Her­lei­tung folgt im Prinzip der für das rechtwinklige sphärische Dreieck.

Der Seitensinussatz

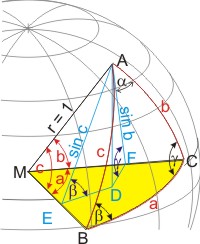
Es sei M der Mittelpunkt auf einer Kugel mit dem Radius r = 1, und das Dreieck ABC ein sphärisches auf der Kugekoberfläche, d. h. die Seiten a, b und c des Dreiecks liegen auf Großkreisen der Kugel. Man fällt das Lot mit dem Fußpunkt D von der Dreiecksecke A auf die Fläche des Kreissegments MBC, das Lot mit dem Fuß­punkt F von A auf den Radius MC, und das Lot (Fußpunkt E) auf MB. Dann verbindet man die Fußpunkte D, E, F in der Seg­ment­ebe­ne (blaue Linien). Man erhält so zwei ebene rechtwinklige Hilfs­dreiecke ADF und ADE (der rechte Winkel ist jeweils am Punkt D).

Da wir uns mit der Einheitskugel beschäftigen, entsprechen die Seitenlängen des sphärischen Dreiecks den Winkeln, die am Mit­tel­punkt von den (punktierten) Verbindungslinien zu den Drei­ecks­ecken eingeschlossen wird. Damit ist im ebenen rechtwinkligen Dreieck AFM die Länge der Kathete AF bekannt: AF = sin b (die Hypothenuse AM = 1!). Und im ebenen Dreieck AEM gilt ebenso: AE = sin c. Diese beiden Seiten sind aber die Hypothenusen in den ebenen blauen Dreiecken. In diesen Dreiecken sind auch die Winkel ∠AED = β und ∠AFD = γ bekannt. Also ist die gemeinsame Kathete AD = sin c · sin β = AD = sin b · sin γ.

In dieser Gleichung bingt man die Sinusse der Seiten b und c auf die eine Seite, und die Sinusse der Winkel β und γ auf die andere: (sin c) ⁄ (sin b) = (sin γ) ⁄ (sin β). Den selben Formalismus kann man auch mit den anderen Ecken des sphärischen Dreiecks durchspielen. Am Ende erhält man:

oder in Worten:

Dem aufmerksamen Besucher dieser Website wird dir Ähnlichkeit zum Sinussatz in der ebenen Tri­go­no­me­trie auffallen. Statt der Seiten im ebenen Dreieck stehen beim sphärischen die Sinusse der Seiten im Verhältnis zu den Sinussen der Winkel.

Der Seitencosinussatz

Analog zur ebenen Trigonometrie gibt es auch einen Seitencosinussatz für das sphärische Dreieck.

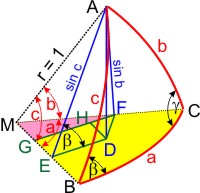
Wir müssen zur Herleitung noch ein paar Hilfsdreiecke in die Ab­bil­dung einzeichnen. Durch das Lot von G auf MB mit dem Fußpunkt G entsteht das ebene Dreieck MFG, und mit dem Lot von D auf FG mit dem Fußpunkt H entsteht das Dreieck HFD. Im Dreieck AEM ist die Strecke EM die Ankathete des Winkels ∠AME = c, die Hy­po­te­nuse MA = r = 1. Also ist EM = cos c. Im Dreieck AMF führt die analoge Überlegung zu MF = cos b. MF ist aber die Hypothenuse im Dreieck FGM, in dem der Winkel ∠FMG = a. Also ist die An­ka­the­te MG = cos a · cos b.
Im Dreieck FDH ist der Winkel ∠DFH = a (weil die Schenkel paarweise aufeinander senkrecht stehen: FG ⊥ BM und FD ⊥ CM). In diesem Dreieck brauchen wir noch die Hypothenuse DF, die wir aus dem Dreieck ADF erhalten: AF = sin b und der Winkel ∠AFD = γ, also ist DF = sin b · cos γ.
Die Strecke ME ist die Ankathete zu ∠c im Dreieck AEM, also ME = cos c (die Hypothenuse AM = r = 1!).

Gleichzeitig ist ME = MG + EG. MG kennen wir schon, und EG = DH (weil FG und DE parallel sind). Im Dreieck DFH kennen wir die Hypothenuse DF = sin b · cos γ und den Winkel ∠DFH = a, also ist die Ge­gen­ka­thete EG = DH = sin a · sin b · cos γ. Aus dem Ausdruck ME = MG + EG erhalten wir durch Ein­set­zen: ME = cos a · cos b + sin a · sin b · cos γ = cos c. Die analoge Argumentation für die anderen Seiten führt zum Seitencosinussatz:

Der Winkelcosinussatz

Der Winkelcosinussatz kann auf ähnliche Weise wie der Seitencosinussatz abgeleitet werden (unter Ver­wen­dung des Polardreiecks). Wir verzichten hier allerdings auf die Herleitung.

Die Hauptaufgaben im schiefwinkligen sphärischen Dreieck

Im Abschnitt "ebene Trigonometrie" hatten wir die Berechnungsmethoden für alle Kombinationen von ge­ge­be­nen und gesuchten Stücken des schiefwinkligen Dreiecks ausgeführt. Die Aufgaben kommen in der Praxis des Navigators eigentlich nur bei der Astronavigation vor.

1. Gegeben sind die drei Seiten a, b, c eines sphärischen Dreiecks, gesucht sind die drei Winkel α, β und γ.
   Zur Lösung werden die Formeln der Seitencosinussatzes nach den Cosinussen der Winkel aufgelöst:
   
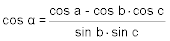
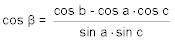
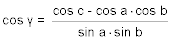
   Die Lösungen sind immer eindeutig.
2. Gegeben sind die drei Winkel α, β und γ eines sphärischen Dreiecks, gesucht sind die drei Seiten a, b, c.
   Die Aufgabe wird mit dem Winkelcosinussatz gelöst und liefert eine eindeutige Lösung, wenn jede Seite kleiner ist als die Summe der beiden anderen und die Summe der Winkel zwichen 180° und 540° liegt. Wir lösen die drei Gleichungen des Winkelcosinussatzes nach den Cosinussen der Sei­ten a, b, c auf, und erhalten drei Formeln, die als Variablen nur die drei Winkel enthalten.
   
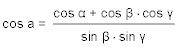
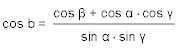
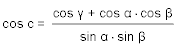
3. Gegeben sind zwei Seiten a und b und der dazwischen liegende Winkel γ, gesucht sind c, α und β.
   Die Aufgabe wird mit dem Seiten­co­sinus­satz und dem Sinussatz gelöst. Hier wird nur die Seite c mit dem Seiten­co­sinus­satz eindeutig berechnet. Die Winkel ergeben nach dem Sinussatz eine oder zwei Lösungen.
   1. Nach dem Seitencosinussatz gilt:
      cos c = cos a · cos b + sin a · sin b · cos γ
   2. Aus dem Sinussatz ergeben sich durch Umformen:
      sin α = (sin a · sin γ) ⁄ sin c
   3. und
      sin β = (sin b · sin γ) ⁄ sin c
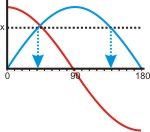   Da die Sinusfunktion (blau) im Bereich bis 180° für zwei ver­schie­dene Winkel den gleichen Funktionswert liefert, gibt es je zwei Lösungen für α und β. Die Cosinusfunktion wechselt im Bereich das Vorzeichen. Daraus folgt: man muss das Vorzeichen beachten und erhält dann eindeutige Lösungen.
4. Gegeben sind 2 Winkel α, β und und die eingeschlossene Seite c, gesucht sind a, b, γ.
   Der Winkel γ ergibt sich nach dem Winkelcosinussatz eindeutig:
   1. cos γ = - cos α · cos β + sin α · sin β · cos c
   2. Die beiden Seiten berechnet man mit dem Sinussatz:
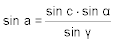
   3. und
      
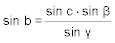
5. Gegeben sind zwei Seiten a, b und ein Gegenwinkel α, gesucht sind c. β, γ.
   
   1. Der Winkel β wird mit dem Sinussatz berechnet: sin β = (sin b · sin α) ⁄ sin a.
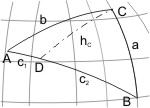   2. Um die Seite c und den Winkel γ zu berechnen, muss das schief­wink­lige sphärische Dreieck ABC durch die sphä­ri­sche Höhe h_C (die liegt auf einem Großkreis durch die Ecke C) in zwei recht­wink­lige Dreiecke ACD und DCB zer­legt werden (die Seite c wird in zwei Teile c₁ und c₂, der Winkel γ in γ₁ und γ₂ geteilt). Man erhält im Dreieck ACD aus den gegebenen Stücken b und α:
      1. tan c₁ = tan b · cos α
      2. cot γ = tan α · cos b
      und im Dreieck DCB:
      3. tan c₂ = tan a · cos β
      4. cot γ₂ = tan β · cos a
      Damit kann man c = c₁ + c₂ und γ = γ₁ + γ₁ berechnen, wenn nicht sin b · sin α > sin a ist: dann hat die Aufgabe keine Lösung! Wenn sin b · sin α = sin a ist das Dreieck ABC recht­wink­lig. Und wenn sin b · sin α < sin a, dann hat sie keine, eine oder zwei Lösungen.
6. Gegeben sind zwei Winkel α, β und eine Gegenseite a, gesucht werden b, c, γ.
   Die Lösung erfolgt nach dem Sinussatz mit der sphärischen Höhe wie die Aufgabe V. Man erhält die Gleichungen:
   1. sin b = (sin a · sin β) ⁄ sin α
   2. tan c₁ = tan b · cos α
   3. cot γ₁ = tan α · cos b
   4. tan c₂ = tan a · cos β
   5. cot γ₂ = tan β · cos a
   6. c = c₁ + c₂
   7. γ = γ₁ + γ₂
   Die Aufgabe hat in der Regel 2 Lösungen.

• Zum Thema gehörende Seiten:
• [sphärische Trigonometrie - Grundlagen]
• [Das rechtwinklige sphärische Dreieck]
• [Das schiefwinklige sphärische Dreieck]
• [Anwendungen der sphärische Trigonometrie] (Orthodrome, Tageslänge, Deklination der Sonne)
• [Anwendungen der sphärische Trigonometrie] (Sonnenhöhe, indischer Kreis)
• [Die Nepersche Regel]
• [Beispielrechnung]
• [Konstruktion mit Projektion der Kugel]