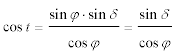Beispielrechnungen zum nautischen Dreieck
Berechnung der Tageslänge
Am 1. Mai 2014 beträgt die Deklination der Sonne δ = 15° 8′ 48,7″ = 15,15°. Für Leipzig (φ = 51° 20′ = 51,33°) sollen die Länge des Tages und die Richtung der Aus- und Untergänge berechnet werden.
Die Formeln wurden bereits abgeleitet. Zunächst wird der Stundenwinkel im Äquatorsystem berechnet nach der Formel:
Mit dem Rechenschieber geht das besonders einfach.
Man stellt den Strich des Läufers über den Wert φ = 51,33° auf der Tangensskala T2 (die beginnt bei 45° und endet bei 84,3 ) und verschiebt die "1" der Zungenskala C unter den Läuferstrich. Nebenbei erfährt man, dass tan 51,33° = 1,25. (Das braucht man nicht zu merken!)
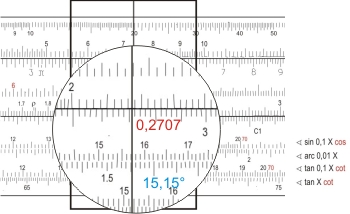 Nun verschiebt man den Läufer über den Wert δ = 15,15° auf der Skala T1 (von 5,5° bis 45°) und liest auf der Körperskala D tan δ = 0,271. Diese Zahl merkt man sich und stellt den Läufer über 0,271 auf der Zungenskala C.
Nun verschiebt man den Läufer über den Wert δ = 15,15° auf der Skala T1 (von 5,5° bis 45°) und liest auf der Körperskala D tan δ = 0,271. Diese Zahl merkt man sich und stellt den Läufer über 0,271 auf der Zungenskala C.
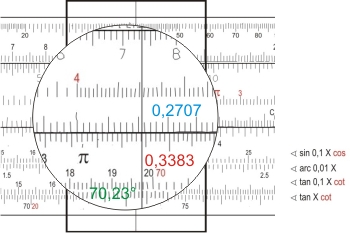 Das Produkt tan φ · tan δ = 0,3383 kann man auf der Körperskala D ablesen, braucht es aber nicht! Denn der Läufer steht ja schon richtig, um auf der Skala "S" den zum cos t gehörenden Winkel (von rechts nach links!) abzulesen: t = 70,23°. Da der Wert des cos t negativ war, ist der gefundene Wert der Ergänzungswinkel des gesuchten. Also: t = 180° - 70,23° = 109,77°.
Das Produkt tan φ · tan δ = 0,3383 kann man auf der Körperskala D ablesen, braucht es aber nicht! Denn der Läufer steht ja schon richtig, um auf der Skala "S" den zum cos t gehörenden Winkel (von rechts nach links!) abzulesen: t = 70,23°. Da der Wert des cos t negativ war, ist der gefundene Wert der Ergänzungswinkel des gesuchten. Also: t = 180° - 70,23° = 109,77°.
Diesen Winkel dividieren wir durch 15 °⁄h und erhalten für die halbe Tageslänge: 7,318 Std. Der Tag am 1. Mai 2014 in Leipzig ist also 14 h 38 m 9,6 s lang.
Schneller geht es nicht — jedenfalls wenn man keine allzu große Genauigkeit braucht.
Mit der halben Tageslänge kann man auch den Zeitpunkt des Sonnenauf- und untergangs angeben. Da die Sonne zu Mittag (= 12 h Ortszeit) kulminiert, liegt der Sonnenaufgang 7 h 19 m vorher, also um 4:41 h (=5:41 h MESZ), und der Untergang um den gleichen Betrag später um 19 h 38 m (20:38 h MESZ).
Die Website APPER.de bietet — neben anderen — den Service der interaktiven Tageslängenberechnung. Das Ergebnis dort für den gleichen Ort und Tag: 14 h 50 m. Der Unterschied dürfte darin beründet sein, dass hier von der Kreisbahn um die Sonne ausgegangen wird, auf der sich die Erde gleichmäßig bewegt. Das ist nicht so. Vielmehr ist die Erdbahn eine Ellipse und die Bahngeschwindigkeit hängt von der Stellung zur Sonne ab — wie Johannes Kepler beweisen konnte. Außerdem geht die hier dargestellte Berechnung davon aus, dass zwischen zwei Sonnenkulminationen genau 24 h vergehen. Auch das ist nicht so. (Ausführliche Erklärungen findet man auf beliebigen Astronomie-Sites.)
Richtung des Sonnenauf- und untergangs
Mit der zweiten Formel findet man die Himmelsrichtung des Sonnenauf- und -untergangs.
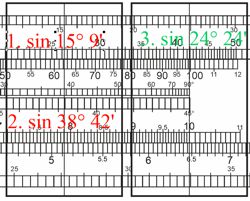 Diese Aufgabe löst man am Bestem mit dem Navigator-Rechenschieber von Unique, da man mit dem Winkelfunktionen dividieren kann. Man stellt den Läuferstrich auf der S1-Skala auf dem Körper über δ = 15,15° = 15° 09′, und mit der Zungenskala S2 den Wert φ = (90° - 51,33°) = 38,7° = 38° 42′ unter den Läuferstrich: dann liest man über "100" auf der Körperskala S1 direkt den Winkel (90° - t) = 24° 24′ = 24,4° ab. Also t = 65,6°.
Diese Aufgabe löst man am Bestem mit dem Navigator-Rechenschieber von Unique, da man mit dem Winkelfunktionen dividieren kann. Man stellt den Läuferstrich auf der S1-Skala auf dem Körper über δ = 15,15° = 15° 09′, und mit der Zungenskala S2 den Wert φ = (90° - 51,33°) = 38,7° = 38° 42′ unter den Läuferstrich: dann liest man über "100" auf der Körperskala S1 direkt den Winkel (90° - t) = 24° 24′ = 24,4° ab. Also t = 65,6°.
Die Sonne geht also bei 65,6° auf (etwas nördlicher als Ost), und sie geht bei (360° - 65,6°) = 294,4° unter (etwas nördlicher als West).
Berechnung der Deklination der Sonne
Zur Berechnung der Deklination der Sonne reicht die Genauigkeit des Rechenschiebers leider nicht aus: man kann ja auf maximal 4 signifikante Stellen rechnen. Das entspräche etwa 10 Bogenminuten. Wir setzen den "Navigator" von Unique ein. (Achtung; die Winkelskalen sind in Grad und Minuten eingeteilt!)
- sin δ = sin λ · sin ε
- ε = 23,5° = 23° 30′
- λ = 136,2869°
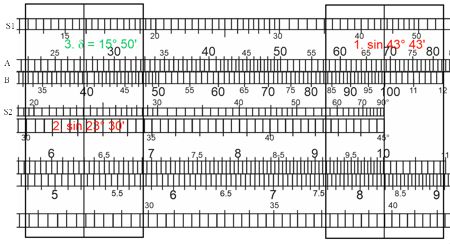
Da die Sinusskala des Rechenschiebers nur bis 90° anzeigt, wenden wir die Phasenregel an: sin (180° ± α) = sin α, und stellen mit dem Läufer den Wert 180° - 136,2869 = 43,7131 = 43° 43′ auf der S1-Skala ein. Unter den Läuferstrich schieben wir die 10 der Zunge, und verschieben den Läufer auf 23° 30′ auf der Skala S2. Auf S1 lesen wir den Wert der Deklination δ = 15° 50′ für den 05.08.2016 ab. Der wahre Wert dürfte bei 16° ± 30′ liegen.
- Zum Thema gehörende Seiten:
- [sphärische Trigonometrie - Grundlagen]
- [Das rechtwinklige sphärische Dreieck]
- [Das schiefwinklige sphärische Dreieck]
- [Anwendungen der sphärische Trigonometrie] (Orthodrome, Tageslänge, Deklination der Sonne)
- [Anwendungen der sphärische Trigonometrie] (Sonnenhöhe, indischer Kreis)
- [Die Nepersche Regel]
- [Beispielrechnung]
- [Konstruktion mit Projektion der Kugel]