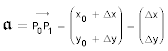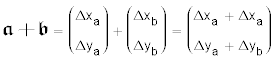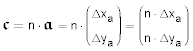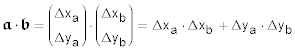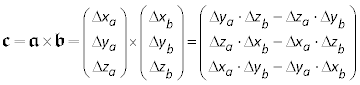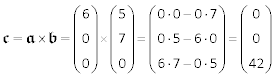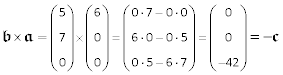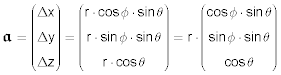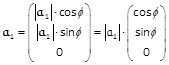Vektoren werden auf dieser Seite mit fetten Buchstaben in der Frakturschrift bezeichnet. Die Kodierung erfolgt mit Unicode-Glyphen 1D565 bis 1D59F. Diese werden mit aktuellen Versionen vieler Browser dargestellt. Nicht dargestellt werden sie mit Windows^® und iOS^® Versionen von Safari^®.

Vektoren

Zur mathematischen Formulierung und Lösung physikalischer Probleme wurden gerichtete Größen ent­wickelt. Die "Vektor Analysis" wurde axiomatisch von Josuah Willard Gibbs im dreidimensionalen Raum formuliert. In der Ana­ly­ti­schen Geometrie werden Vektoren in einem karthesischen Ko­or­di­na­ten­sy­stem als Pfeile repräsentiert. Der Betrag a eines Vektors 𝖆 ist die Läge des Pfeils a = |𝖆|, also eine Strecke.

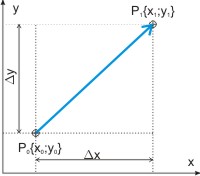Geht man in einem karthesischen Koordinatensystem von einm Punkt P₀ mit den Koordinaten x₀ und y₀ aus und verschiebt ihn um Δx und Δy zu einem Punkt P₁ mit den Koordinaten x₁ = x₀ + Δx und y₁ = y₀ + Δy so ist diese Verschiebung ein Vektor. P₀P₁ = 𝖆 = {x₀ + Δx; y₀ + Δy} ist also auch eine Repräsentation des Vektors im kathesischen Koordinatensystem.

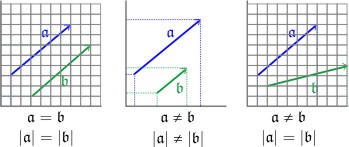
Zwei Vektoren 𝖆 und 𝖇 sind genau dann gleich, wenn ihre Repräsentanten (Pfeile) in Betrag und Richtung über­ein­stimmen. Eine zu den Achsen pa­ral­lele Verschiebung im Koordinatensystem, also die Änderung der Ko­or­di­na­ten x₀ und y₀ von P₀, verändert die Vektoren nicht. Der Vektor 𝖆 ist also unabhägig von seiner Lage im Koordinatensystem, und er ist nur mit Δx und Δy eindeutig beschrieben. Zieht man immer die Koordinate des Anfangs von der der Spitze ab, ist auch die Richtung des Vektors in der Angabe enthalten. Den Winkel α, den der Vektor mit der positiven x-Achse einschließt erhält man dann mit:

• tan α = Δy ⁄ Δx (Definition der Winkelfunktion)

• (|𝖆|)² = (Δx)² + (Δy)² (Satz des Pythagoras)

Vektoraddition

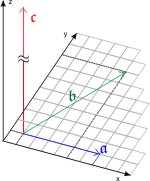
Man kann Vektoren addieren, in dem man die sie so anordnet, dass das stumpfe Ende des einen an der Spitze des anderen hängt. Das Additionsergebnis ist der Vektor, der vom stumpfen Ende des ersten zum Spitze des zweiten reicht. Dabei ist das Ergebnis unabhängig von der Reihenfolge: 𝖈 = 𝖆 + 𝖇 = 𝖇 + 𝖆. In Matrixschreibweise:

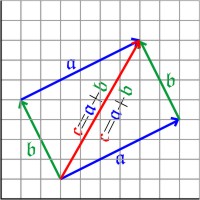In der rechten Abbildung ist:

• Δx_𝖆 = 6,
• Δy_𝖆 = 3,
• Δx_𝖇 = -2,
• Δy_𝖇 = 4,
• Δx_𝖈 = 4,
• Δy_𝖈 = 7,
• 

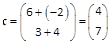
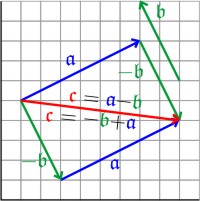Zur Subtraktion addiert man einfach den Vektor, der die umgekehrte Richtung hat, also -𝖇 = {2; -4}:
𝖈 = {6; 3} + {2; -4} = {6 + 2; 3 - 4} = {8; -1}.

Aus der Umkehrung der Vektoraddition leitet man die Vektorzerlegung ab. Man kann jeden Vektor in zwei vektorielle Komponenten zerlegen, die parallel zu jeweils einer der Ko­or­di­na­ten­sy­stem­ach­sen liegen. Das kann zu übersichtlicheren Be­rech­nun­gen führen, wie z. B. beim Drehimpuls oder bei der Zusammensetzung des Win­des beim Se­geln aus den zwei Komponenten Fahrtwind und wahrer Wind.

Multiplikationen von Vektoren

Multiplikation mit einer Zahl

Multipliziert man einen Vektor 𝖆 mit einer Zahl n, so entspricht das Ergebnis der n-fachen Addition des Vektors: 𝖈 = 𝖆 + 𝖆 + 𝖆 + 𝖆 + … = n · 𝖆. Das Ergebnis ist wieder ein Vektor.

Skalarprodukt von Vektoren

Die Multiplikation zweier Vektoren zu einem Skalar wird häufig in der Physik benötigt. Die ungerichtete Größe (Skalar) "Arbeit A" ist Produkt der Vektoren Kraft 𝕶 und Weg 𝖘: A = 𝕶 · 𝖘.

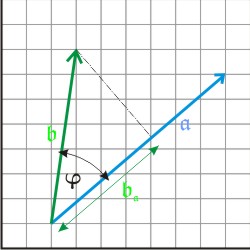Geometrisch ist das Skalarprodukt die Fläche des Rechtecks, aus einem Vektor und der Projektion des zweiten Vektors auf den ersten. Diese Fläche errechnet sich aus dem Betrag des Vektors 𝖆 und dem Betrag der Projektion 𝖇_𝖆 des Vektors 𝖇 auf 𝖆.

Die Projektion 𝖇_𝖆 ist nach der Definition der Winkelfunktionen:

• 𝖇_𝖆 = 𝖇 · cos φ

Gibbs definiert das Skalarprodukt als:

• 13. Def. — The direct product of α and β (written α · β ) is the scalar quantity obtained by multiplying the product of their magnitudes by the cosine of the angle made by their directions. [1]
• 𝖆 · 𝖇 = |𝖆| · |𝖇| · cos φ.

Die Formel des Skalarprodukts in Matrixschreibweise lautet:

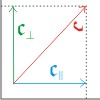
Hier führen wir den Einheitsvektor 𝖆⁰ ein: 𝖆⁰ = 𝖆 ⁄ |𝖆|. Seine Länge wird ge­schick­ter­wei­se den Ein­hei­ten auf den Koordinatenachsen gleichgesetzt, also 𝖆⁰_∥ der Einheit auf der x-Achse und  𝖆⁰_⊥ der auf der y-Achse.

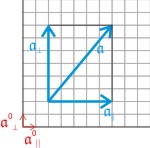Da man jeden Vektor in zwei Komponenten zerlegen kann, die jeweils parallel zu den Achsen des Koordinatensytems sind, kann man jede der Komponeten als Skalarprodukt aus einer (reelen) Zahl i, j und dem Einheitsvektor darstellen.

• 𝖆 = 𝖆_∥ + 𝖆_⊥
• 𝖆_∥ = i · 𝖆⁰_∥
• 𝖆_⊥ = j · 𝖆⁰_⊥

Vektormultiplikation

Gibbs definiert das Vektorprodukt als:

• 14. Def. —The skew product of α and β (written α × β) is a vector function of α and β. Its magnitude is obtained by multiplying the product of the magnitudes of α and β by the sine of the angle made by their directions. Its direction is at right angles to α and β, and on that side of the plane containing α and β (supposed drawn from a common origin) on which a rotation from α to β through an arc of less than 180° appears counter-clockwise.
  The direction of α × β may also be defined as that in which an ordinary screw advances as it turns so as to carry α toward β.
  Again, if α be directed toward the east, and β lie in the same horizontal plane and on the north side of α, α × β will be directed upward. [1]

Das Produkt zweier Vektoren 𝖆 × 𝖇 ist ein Vektor 𝖈, der senkrecht steht auf der von den beiden Mul­tip­li­kan­ten aufgespannten Ebene. Seine Länge entspricht zah­len­mäßig der Fläche des Parallelogramms zwischen den Mul­ti­pli­kan­ten (|𝖆| · |𝖇| · sin φ)

Die Richtung des Produktvektors 𝖈 ist durch ein orientiertes Rechts­sys­tem gegeben. Anschaulich macht man es sich mit den Fingern der rech­ten Hand. Hinweis: Der Daumen deutet in die Richtung des ersten Glie­des des Vektorproduktes, der Zeigefinger in Richtung des zweiten; dann zeigt der Mittelfinger die Richtung des Vektorproduktes an.

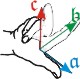
Interessanterweise hängt die Richtung des Vektorprodukts von der Reihenfolge der Multiplikanten ab!

• 𝖈 = 𝖆 × 𝖇
• − 𝖈 = 𝖇 × 𝖆

Das Vektorprodukt von parallelen (oder antiparallelen) Vektoren ist Null, denn es wird keine Fläche zwi­schen ihnen aufgespannt:

• 𝖆 × 𝖆 = 𝖆 × (− 𝖆) = 0.

Mit 𝖆 {6;0;0} und 𝖇 {5;7;0} ergibt sich für 𝖈:

Vektoren im Kugelkoordinatensystem

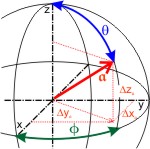Für die Betrachtung von Drehbewegungen ist es vorteilshaft, die Vektoren in räumlichen Polarkoordinaten darzustellen. Um einen Punkt auf der Kugeloberfläche eindeutig zu beschreiben, braucht man neben dem Kugelradius r zwei Winkel Φ und θ, die am Mittelpunkt der Kugel aus gemessen werden. (Der Segler kennt das von den Ortskoordinaten!) Der Ortsvektor 𝖆 {Δx;Δy;Δz} muss also mit seiner Länge r = |𝖆| und zwei Winkeln angegeben werden. Es bieten sich die Winkelfunktionen an:

• Δx ⁄ r = cos Φ · sin θ ⇒ Δx = r · cos Φ · sin θ
• Δy ⁄ r = sin Φ · sin θ ⇒ Δy = r · sin Φ · sin θ
• Δz ⁄ r = cos θ ⇒ Δz = r · cos θ

• sin (90° - θ) ⁄ r = Δz ⁄ r  = cos θ ⇒ Δz = r · cos θ

• cos (90° - θ) ⁄ r = a′ ⁄ r  = sin θ ⇒ a′ = r · sin θ

• cos Φ = Δx ⁄ a′ = Δx ⁄ (r · sin θ) ⇒ Δx = r · cos Φ · sin θ
• sin Φ = Δy ⁄ a′ = Δy ⁄ (r · sin θ) ⇒ Δy = r ·sin Φ · sin θ

Differenzieren von Vektoren

Das Differenzieren von Vektoren beruht im Grunde auf der Zerlegung eines Vektors in seine drei kar­the­si­schen Komponenten und dem Differenzieren der Komponenten, die man dann durch Vektoraddition wieder zum Ergebnisvektor zusammensetzt.

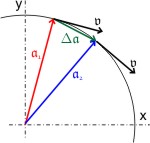Ein Punkt bewege sich mit konstanter Geschwindigkeit 𝖛 auf einem Kreis um den Ursprung eines karthesischen Koordinatensystems. Sein Ort wird durch Vektor 𝖆 im Ursprung beschrieben. Zum Zeitpunkt t₁ sei sein Ort die Spitze des Vektors 𝖆₁ (rot) und zum Zeitpunkt t₂ stehe er bei 𝖆₂ (blau). Er hat sich also in der Zeit Δt = t₂ - t₁ um den Kreisbogen über der Kreissehne, die die Spitzen von 𝖆₁ und 𝖆₂ verbindet, bewegt. Für kleine Winkeländerungen kann man den Unterschied der Längen der Sehne und des Kreisbogens vernachlässigen: Δ𝖆 = 𝖆₂ - 𝖆₁. Die Geschwindigkeit des Punktes ist definiert als 𝖛 = Δ𝖆 ⁄ Δt. Läßt man den Weg nahe Null zu, schreibt man das Differenzial 𝖛 = d𝖆 ⁄ dt: der Geschwindigkeitsvektor ist die zeitliche Ableitung des Ortsvektors 𝖆 eines Punktes auf der Kreisbahn. Der Geschwindigkeitsvektor steht senkrecht auf dem Ortsvektor, da er tangential zur Kreisbahn liegt.

Die polaren Koordinaten des Vektors 𝖆₁ sind Δx = |𝖆₁| · cos Φ und Δy = |𝖆₁| · sin Φ.

Quellen

1. Josiah Willard Gibbs: Elements of Vector Analysis, (Eigenverlag) New Haven 1881-1884.
2. Edwin Bidwell Wilson: Vector Analysis, Founded upon the Lectures of J. Willard Gibbs, New York, London, 1902.
3. A. Föppl: Rechnen mit Vectorgrössen in der Physik; in: Einführung in die Maxwell′sche Theorie der Elektricität, Leipzig 1894.