Vektoren
Vektoren sind mathematische Elemente, für die Rechenregeln der Vektoralgebra gelten. Diese Rechenregeln kann man verstehen, wenn man die üblichen Regeln des täglichen Lebens mit einer Richtung der Elemente verknüpft. Eine gute Assoziation für Vektoren - und die grafische Repräsentation - sind Pfeile. (Die üblichen) ganzen Zahlen sind dann analog Strecken.)
|
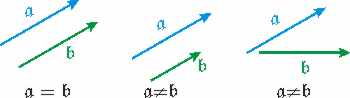
Zwei Vektoren (Pfeile) a und b sind nur dann gleich, wenn sie in Richtung und Länge gleich sind. |
|
Vektoraddition |
|
|
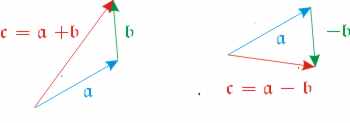
Man kann Vektoren addieren, in dem man die sie so anordnet, dass das stumpfe Ende des einen an der Spitze des anderen hängt. Das Additionsergebnis ist der Vektor, der vom stumpfen Ende des ersten zum Spitze des zweiten reicht. Zur Subtraktion addiert man einfach den Vektor, der die umgekehrte Richtung hat. |
|
|
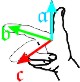
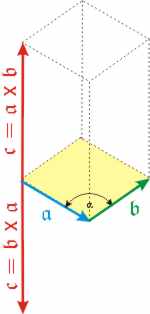
Das Produkt zweier Vektoren steht senkrecht auf der von den beiden Multiplikanten aufgespannten Ebene. Seine Länge entspricht zahlenmäßig der Fläche des Parallelogramms zwischen den Multiplikanten (a·b·sinα) Die Richtung des Produktvektors ist durch ein orientiertes Rechtssystem gegeben. Anschaulich macht man es sich mit den Fingern der rechten Hand. Hinweis: Der Zeigefinger deutet in die Richtung des ersten Gliedes des Vektorproduktes.
Interessanterweise hängt die Richtung des Vektorprodukts von der Reihenfolge der Multiplikanten ab. Das Vektorprodukt von parallelen (oder antiparallelen) Vektoren ist Null, denn es wird keine Fläche zwischen ihnen aufgespannt. |
|
© Rainer Stumpe, URL: http://www.rainerstumpe.de/