Gezeitenvorhersage

Grundlegendes Modell

Im "Lehrbuch der Navigation", herausgegeben vom Reichs-Marine-Amt, 2. Auflage Berlin 1906, fand ich eine interessante Anleitung zur Vorausberechnung der Gezeiten. Der Anfrage eines Besuchers meiner Website entnehme ich, dass diese Berechnungsmethode gelegentlich in Segelschein-Prüfungen gefragt wird.

Das zugrundeliegende Modell geht — physikalisch unrichtig — davon aus, dass die Gezeiten durch die Anziehung von Sonne und Mond bestimmt wird. Da die Anziehungskraft der Sonne nur ¹/_2,17 der des Mondes beträgt, beschränkt man sich auf den Einfluss des Mondes.

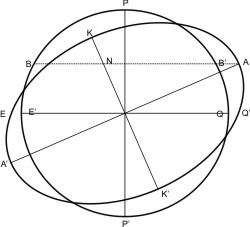
Nach dieser Vorstellung bilden die Wassermassen der Ozeane ein Ellipsoid AKA'K', das zum Mond bzw. zur Sonne ausgerichtet ist. EQ sei der Äquator, PP' die Erdachse. Die große Achse AA' des Ellipsoid ist zum Mond bzw. zur Sonne gerichtet, die kleine KK' schließt mit der Erdachse einen Winkel von 23½° ein. Auf allen Meridianpunkten, die über der Linie AA' liegen, ist Hochwasser, auf dem Großkreis über KK' ist Niedrigwasser.

Ein Punkt Q auf dem Äquator hat zweimal am Tag Hochwasser: einmal in Q und dann wenn der Punkt durch die Drehung der Erde nach E gewandert ist. Ein Punkt zwischen Pol P und Äquator, z. B. B, hat zwei verschieden hohe Hochwasser, denn der Abstand zum Ellipsoid ist in den Positionen B und B' unterschiedlich. Am Pol P ändert sich der Wasserstand nicht (da ist das Wasser ja auch gefroren ;)).

In diesem Modell der "Mondtide" ist es möglich, die Gezeitenvorhersage auf die Kenntnis der Mond­phase zu reduzieren. Allerdings nicht ganz: man braucht noch ein paar empirische Daten, z. B. die "Springverspätung" am Ort, für den man die Gezeit berechnen will. Und die findet man in den "Gezeitentafeln". die das Bundesamt für Seeschifffahrt und Hydrographie (BSH) jährlich herausgibt.

Schauen wir uns zunächst das Modell etwas näher an.

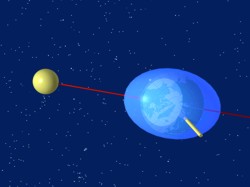
Die lange Achse des Rotationsellipsoids (hier rot gezeichnet) weist immer auf den Mond zu. Wegen der Neigung der Erdachse zur Mondbahn (näherungsweise identisch zur Ekliptik) hat auch diese Achse des Ellipsoids eine im Verlauf eines Mondumlaufes veränderliche Neigung zur Erdachse. So entstehen unterschiedlich hohe Tiden während des Mondumlaufes.

Wenn man also die Stellung der Erdachse kennt (aus dem Tagesdatum) und weiß, wieviel Zeit seit der letzten Springtide vergangen ist, kann man die Höhe des Hochwassers berechnen.

Allerdings tritt die Springtide in der Realität nicht zum Zeitpunkt des Meridiandurchganges von Voll- bzw. Neumond ein, sondern zu einer von der geografischen Lage abhängigen späteren Zeit, der "Springverspätung". Diese "Springverspätung" wird empirisch ermittelt und für das jeweilige Jahr vom BSH veröffentlicht.

Man muss nur herausfinden, wann Voll- oder Neumond ist. Da auch der Mond den Keplerschen Gesetzen unterliegt, und seine Bahngeschwindigkeit schwankt, benötigt man Näherungen. Genaueres im Abschnitt "Berechnung der Gezeit nach RMA" weiter unten.

Die Gezeitentafeln des BSH

Die Gezeitetafeln haben drei Teile: "Teil I: Ausführliche Vorausberechnung für europäische Bezugsorte", "Teil II: Gezeitenunterschiede für die europäischen Anschlussorte" und "Teil III: Hilfs-Tafeln, Grafik und Flusspläne".

Wie die Tafeln des ersten Teils aussehen und wie man sie zur Berechnung von Wasserständen zu beliebigen Zeiten verwendet, wurde bereits erläutert. Wenden wir uns also dem Teil 3 zu. Hier werden die (empirischen) Grunddaten zur Berechnung der Tafeln in den Teilen 1 und 2 gelistet. Gelegentlich wird die Berechnung auf dieser Basis in Segelscheinprüfungen gefragt.

Der Teil III der Gezeitentafeln enthält folgende Tabellen:

1. Gezeitengrundwerte europäischer Bezugsorte.
   Die Angeben sind:
   • Bezugsort
   • Springverspätung
   • Mittlere Steigdauer
   • Mittlere Falldauer
   • MSpHW
   • MNpHW
   • MSpNW
   • MNpNW
   • Angaben über die Berechnungsart (harmonisches bzw. nichtharmonisches Verfahren) und die Organisation, die die Berechnung durchgeührt hat.
2. Spring-, Mitt- und Nipp-Zeiten für jeden Tag des Jahres.
3. Mondphasen. (Datum und Uhrzeit: Erstes Viertel, Vollmond, Letztes Viertel, Neumond)
4. Zeit des Durchganges des Mondes durch den Nullmeridian.
5. Tafel zur Verbesserung der Hoch- und Niedrigwasserstände.
6. wegen halbmonatlicher Ungleichheit.

Die Rechenbeispiele in den Gezeitentafeln des BSH gehen nicht wesentlich über das auf dieser Website dargestellte hinaus.

Berechnung der Gezeit nach RMA

Um die Gezeit mit nicht zu großem Fehler vorausberechen zu können, braucht man folgende Angaben:

1. Die mittlere Sonnenzeit der Mondkulmination am Vorhersageort.
2. Das mittlere Mondflutintervall.
3. Die halbmonatliche Ungleichheit in Zeit und Höhe.

Die mittlere Sonnenzeit der Mondkulmination berechnet man aus der Tabelle "Zeit des Durchganges des Mondes durch den Nullmeridian" (Tabelle 4, BSH Teil III, s. o.) nach der Formel:

m.O.Zt. ☾ Kulm. = m.Zt. ☾ Kulm.i.Gr. ± λ · Änderung.f.1°

λ steht für die geographische Länge des Vorhersageortes. Die täglich unterschiedliche Änderung der Kulminationszeit entnimmt man dem Nautischen Jahrbuch. Sie hängt mit der - im Vergleich zur Sonne - schnelleren Bewegung des Modes und der Schwankung seiner Umlaufgeschwindigkeit zusammen.

Die mittlere Sonnenzeit der Mondkulmination muß man noch in (Zeitzonen-) Uhrzeit umrechnen!

Das mittlere Mondflutintervall ist das (Zeit-) Intervall der mittleren wahren Hoch- und Niedrig­wasser­zeiten und der wahren Zeit der Mondkulmination. Es wird durch Messungen mindestens einer halben Lunation (=14 3/4 Tage) oder ihrer Vielfachen bestimmt. Auch die Springhochwasser tritt um einen Zeitraum, das Alter der Gezeit, nach Voll- bzw. Neumondes ein.

Da man in diesem Modell das Eintreten des Springhochwassers mit dem Meridiandurchgang des Voll- bzw. Neumondes in Beziehung setzt, muss man eine Zuordung eines der beiden täglichen Hochwasser zur Kulmination treffen. Man wählt es so, dass das mittlere Mondflutintervall und die halbmonatliche Ungleichheit möglichst nahe am Alter der Gezeit ist. Wenn man die Vorausberechnung nach diesem Prinzip macht, ist der Fehler der Flutvorhersage sehr gering.

Der mittlere Wasserstand ergibt sich aus dem Mittelwert der Hoch- und Niedrigwasserstände, die zur Ermittlung des mittleren Mondflutintervalls herangezogen worden sind.

Zur Bestimmung der halbmonatliche Ungleichheit in Zeit und Höhe teilt man die Mondflutintervalle und die Höhen der Hoch- und Niedrigwasser einer möglichst großen Anzahl halber Mondmonate in 12 Gruppen, die den Mondkulminationszeitbereichen 00:00h bis 00:59h, 01:00 bis 01:59h, usw. entsprechen. In jeder Gruppe bildet man den Mittelwert der Daten, und erhält so die mittleren Mondflutintervalle und Höhen der Kulminationszeiten 00:30h, 01:30h, usw.. Die Unterschiede dieser Mittelwerte von den allgemeinen Mittelwerten der Mondflutintervalle und Höhen ergeben die mittlere halbmonatliche Ungleichheit in Zeit und Höhe. Diese Werte werden in ein Diagramm eingetragen (x-Achse: Kulminationszeit, y-Achse: mittlere halbmonatliche Ungleichheit), dem man die halbmonatliche Ungleichheit für die Kulminationszeit entnimmt, die zum mittleren Mondflutintervall gehört.

Es ist möglich, die Werte noch um die tatsächlichen Entfernungen Erde-Mond zu verbessern (im RMA "Parallaxe" genannt). Dazu braucht es aber viele Meßwerte, die dann in jahreszeitliche Gruppen zusammengefaßt werden aus denen man einen Mittelwert nimmt. Außerdem kann man noch die tägliche Ungleichheit (d. i. der Unterschied der Höhen der beiden täglichen Tiden) berücksichtigen. Dazu verbessert man die beobachteten Mondflutintervalle und Höhen mit der halbmonatlichen Ungleichheit und der Parallaxe. Die Werte enthalten dann nur noch eine Abhängigkeit vom mittleren Mondflutintervall und der täglichen Ungleichheit. Die halbe Differenz der zur oberen und unteren Kulmination gehörenden Mondflutintervalle und Höhen ist die tägliche Ungleichheit.

Rechenbeispiel

Da die erforderlichen Gezeitenwerte heute nicht mehr verfügbar sind, ist dieses Beispiel dem Buch direkt entnommen.

1. Gesucht wird die Zeit des Hochwassers in Cuxhaven am 17. Juli 1904 (λ = 8° 42' O).

   				Untere Kulm.	Obere Kulm.
   m. Zt.	☾ Kulm. in Gr.	17. VII	=	3 h 38 m	16 h 5 m
   	Änd. f. -9°		=	-1	-1
   m. O. Zt.	☾ Kulm. a. O		=	3 h 37 m	16 h 4 m
   	(Ztgl.)		=	(+6)	(+6)
   (w. O. Zt	☾ Kulm. a. O)		=	(3 31)	(15 58)
   Hafenzeit von Cuxhaven			=	0 49	0 49
   halbmonatl Ungleichheit			=	-49	-55
   m. O. Zt. d.	Hochwassers	17. VII	=	3 37	15 58

   Ab 1906 werden die Werte des Meridiandurchganges des Mondes im Nautischen Jahrbuch für europäische Küstenorte um die halbmonatliche Ungleichheit korrigiert. Das vereinfacht die Rechnung.

2. 			Untere Kulm.	Obere Kulm.
   m. Zt. ☾ Kulm. in Gr. verb. f. halbmon. Ungl.	17. VII.	=	2h 52m	15h 14m
   Änd. f. -9°		=	-1	-1
   m. O. Zt. ☾ Kulm. a. O. verb. f. halbmon. Ungl.		=	2 51	15 13
   Hafenzeit von Cuxhaven		=	0 49	0 49
   m. O. Zt. d. Hochwassers in Cuxhaven	17. VII.	=	3 40	15 02

   Der Zeitunterschied des Eintretens des Hochwassers in Cuxhaven beruht auf der Korrektur der Werte im Nautischen Jahrbuch, wodurch Ungenauigkeiten entstehen, wenn sich die halbmonatliche Ungleichheit rasch ändert.

3. Gesucht werden Zeit und Höhe des Hochwassers.

   Das mittlere Mondflutintervall, bezogen auf die fünfte vorhergehende Kulmination, beträgt für Cuxhaven 2d 1h 55m, die mittlere Höhe von Hochwasser für Juli ist 3,17 m über dem Niveau des mittleren Springniedrigwasser.

   Aus dem Kalender der Gezeitentafeln:

   Mittl. Zeit d. ☾ Kulm. I. Gr.	15.VII.	=	1h 47m	und	14h 16m
   ☾ δ	15.VII.	=	12,9° N		11,0° N
   ☾ Parallaxe	15.VII.	=	60,5'	60,5'
   ☾ δ 10.VII. 21h 53m		=	17,6°
   ☾ δ 11.VII. 10h 21m		=	18,2°

   Änd. d. m. O. Zt. d. ☾ Kulm. f. -9° Lg. = -1m, Zeitgleichung = + 6m.

   m.Zt. ☾ Kulm. i. Gr. 15.VII.	=	1h 47m	unt. Kulm.	14h 16m	ob. Kulm.
   Änd. f. -9°	=	- 1		- 1
   m.O.Zt. ☾ Kulm. a. O. 15.VII.	=	1h 46m		14h 15m
   Zeitgleichung	=	+6		+6
   w. O.Zt. ☾ Kulm. a. O. 15.VII.	=	1h 40m		14h 9m

   Mittl. Mondflutint. u. mittl. Höhe	=	2d 1h 55m	3,17 m	2d 1h 55m	3,17 m
   halbmonatl. Ungleichheit	=	-14	+0,12	-22	+0,08
   Verbesserung für Parallaxe	=	+4	+0,08	+6	+0,08
   Verbesserung für Abweichung	=	+1	+0,01	+2	+0,01
   tägliche Ungleichheit	=	+7	-0,14	-7	+0,14
   Zeitgleichung	=	+6		+6
   Hochwasser: m. O.Zt. 17:VII.	=	3h 39m	3,24 m	3h 48m	3,48 m

   Die Werte der halbmonatl. Ungleichheit, der Verbesserungen für Parallaxe und Abweichung, und die tägliche Ungleichheit entnimmt man Tabellen im Nautischen Jahrbuch.