Ioannis Verneri: De Triangulis Sphæricis, Liber QuatuorLiber QuartusPropositio prima.In dato sphærico triangulo duobus segmentis, quorum utrumque fuerit quadrante minus, propositum aliquem comprehendentibus angulum, si super unius eorundem segmentorum tanquam polo magnus scribatur circulus, et super altero quidem eiusdem segmenti termino, spatio autem alterius duorum iuxta eundem angulum segmentorum parvus describatur circulus, ex quo circumferentia proposito angulo similis auferatur, et a termino sinus versi eandem subtendentis circumferentiam perpendicularis ad magni circuli planum deducatur, erit eadem perpendicularis æqualis sinui recto complementi eius segmenti, quod in dato triangulo eundem propositum subtendit angulum.
Coniunctis itaque CI, LK rectis, et quia planum quadrantis ACE erectum est ad planimi circuli DEF, igitur rectus sinus CL ad idem planum circuli DEF erigitur; nam rectus sinus CL perpendicularis est ad communem sectionem duorum planorum, quadrantis videlicet ACE et magni circuli DEF. Est autem IK per constructionem ad idem planum DEF perpendicularis; ergo perpendicularis IK et sinus rectus CL sunt paralleli per propositionem sextam libri undecima elementorum Euclidis. Et quia per diffinitionem CI rectus est sinus segmenti HC, et planum parvi circuli GCH erectum est plano circuli ABD, igitur duorum angulorum CIK et IKL uterque rectus per tertiam diffinitionem eiusdem libri undecimi; nam HI pars est communis sectionis duorum planorum circuli magni ABD et circuli parvi GCH. Et quia utraque rectarum linearum CI, KL in eodem sunt plano IK, CL rectarum linearum per septimam propositionem eiusdem libri undecimi, igitur per XXVIII libri primi eorundem elementorum duæ rectæ CI, KL sunt parallelæ. Igitur quadrilaterum CIKL est paralleogrammum. Ergo IK perpendicularis æqualis est sinui recto CL; nam per XXXIV propositionem primi libri eorundem elementarum "parallelogramorum locorum latera, quæ ex opposito, et anguli, æqualia sunt adinvicem". Igitur in dato sphærico triangulo duobus segmentis, etc.; quod oportuit demonstrare. Propositio secunda.Datis tribus lateribus propositi trianguli sphærici angulum datum efficere duobus contentum segmentis, quorum utrumque quadrante minus extiterit. Sit ergo alterum segmentorum, quæ propositum continent angulum, AB; atque maximus circulus, cuius segmentum AB portio existit, sit ABCDEF. Et descripti super A polo maximi circuli dimetiens sit CE, atque super B polo maximi descripti circuli dimetiens sit DF. Hi duo dimetientes se invicem secabunt in centro sphæræ, quod sit G. Sit autem reliquum segmentorum, a quibus propositus angulus continetur, æquale segmento BH, quod subiiciatur esse maius circumferentia AB, minus autem complemento eiusdem circumferentiæ AB. Igitur punctus H necessario cadet inter B, C signa. Et a puncto H ipsi DGF dimetienti parallela agatur HI. Atque segmenti IFE sinus rectus sit IK; et ipsius parallela sit acta LM æqualis sinui recto complementi tertii lateris, quod in proposito triangulo sphærico subtenditur ei angulo, quem datum oportet efficere. Deinde CGE diametro parallelus agatur HNO, secans LM super N et IK super O signo.
Datis igitur tribus lateribus propositi trianguli sphærici, etc.; quod oportuit demonstrare. Lemma sive assumptam.Quod autem IO et LN rectæ lineæ datæ sint, sic perspicuum fiet. Nam IOK datur; est enim IOK sinus IEF segmenti per constructionem quoque dati; nam ipsum componitur ex segmento EF æquali ipsi AB segmento, et FI segmento, quod æquale est DH complemento segmenti BH, quod ex hypothesi æquatur alteri laterum angulum subiectum ad B continentium. Et LM quoque datur; nam ipsa æqualis est sinui recto complementi circumferentiæ propositum ad B angulum subtendentis. Sunt autem et OK, NM rectæ datæ; utraque enim æqualis est sinui recto circumferentiæ HC, quæ complementum existit per constructionem ABH segmenti. Igitur ex IOK et LNM sublatis OK, NM erunt reliquæ IO, LN datæ; quod oportebat manifestum perspicuumque efficere. Correlarium.Hinc etiam erit perspicuum, in subiecto triangulo sphærico trium datorum segmentorum, quorum duo propositum angulum, quem datum efficere oportet, continentia utraque sint quadrante minora, propositus ad B angulus unica fiet perspicuus proportione, in qua primus terminus sit dimidium ipsius IO, secundus terminus LN, tertius terminus FG semidiameter sphæræ sive sinus totus, quartus ipsius DGF dimetientis particola DP existens sinus versus circumferentiæ maximi circuli, cuius dimetiens DGF, quæ quidem circumferentia similis est in parallelo IH circumferentiæ, cuius versus sinus est HL, qua quidem circumferentia ex semicirculo dempta remanebit segmentum maximi circuli æquale proposito ad B angulo sphærico. Et ut liquidius fiat, quod illatum fuit correlarium, sit igitur IO ad NL, seu sicut IH ad HL, sic etiam fiat DF ad DP; et dimidium ipsius IO sit IQ; et quia IQ ad IO est sicut GF ad FB, et IO ad LN sicut FD ad DP, igitur ex æquali IQ ad LN erit sicut FG semidiameter sphæræ, seu sinus rectus integer, ad DP, Sed DP sinus versus est circumferentiæ, qua maximo semicirculo sublata relinquitur circumferentia æqualis sphærico angulo ad B proposito. Igitur in triangulo sphærico trium datorum segmentorum, quorum duo propositum angulum includant, et cetera; quod est correlarium inferendum. Propositio tertia.Si autem in dato triangulo sphærico trium datorum segmentorum duo segmenta propositum continentia fuerint æqualia, idem propositus angulus datus angulus erit. Hæc propositio per præmissam et subsequentes quoque ostendi poterit. Nam si uniuscuiusque æqualium segmentorum complementum maius fuerit octava parte circui magni, id est maius gradibus XLV, ipsa propositio fiet per præcedentem propositionem; sin autem æcquale, per sequentem propositionem; aut [si] minus octava parte maximi circuli, sive gradibus XLV, problema fiet per quintam propositionem. Propositio quarta.At si alterum duorum segmentorum, quæ propositum ad B angulum comprehendunt, æquale fuerit complemento circumferentiæ AB, id est segmento BC.
Et quia, velut prius ostenditur, triangulus CKL similis triangulo CHI, ergo per propositionem quartam libri sexti elementorum ratio HI ad KL erit sicut ratio ipsius HC ad CK. Et ex dimetiente FD auferatur DM secundum rationem HI ad KL. Igitur HI ad KL est sicut FD ad DM, Et dimidia ipsius HI sit HN. Et quia per constructionem FG dimidium est ipsius DGF dimetientis, ergo HN ad HI est sicut FG ad FGD. Igitur ex æquali HN ad KL est sicut FG ad DM. In hac autem proportione tres priores termini dati sunt. Nam HN dimidium est ipsius HI, quæ rectus est sinus circumferentiæ EFH per constructionem quoque datæ; nam ipsa componitur ex duplo circumferentiæ EF, id est ex duplo ipsius circumferentiæ AB, Et KL æqualis est sinui recto complementi circumferentiæ per hypothesim datæ et subtendentis angulum ad B propositum. Et FG sinus totus. Ergo et quartus terminus DM datus est. Et quoniam per constructionem ratio FD ad DM est sicut ratio ipsius HO CK — est autem GK sinus versus circumferentiæ in parallelo HC similis segmento magni circuli, relinquitur circumferentia æqualis angulo ad B proposito —, igitur FM sinus versus est propositi anguli ad B. Ergo angulus ad B propositus est datus; quod oportuit demonstrare. Correlarium.Inde perspicuum fit, quod hoc modo propositus ad B angulus dabitur una proportione, cuius primus terminus est dimidium recti sinus duplæ circumferentiæ minoris duorum laterum propositum angulum comprehendentium. Secundus terminus est sinus rectus complementi circumferentiæ propositum subtendentis angulum. Tertius terminus est sinus totus, id est dimidium dimetientis maximi circuli. Quartus terminus est versus sinus circumferentiæ, qua sublata ex semicirculo propositus relinquitur angulus. Prioribus autem terminis per prius ostensa datis, et quartus terminus datur, videlicet versus sinus circumferentiæ, qua ex semicirculo dempta propositus relinquitur angulus. Aliter propositio hæc ostenditur.
Igitur per propositionem libri III elementorum Euclidis AC segmentum angulo ABC subtensum bifariam secetur in puncto D; et per B, D signa magni orbis sectio BD describatur. Et quia duo maximorum in sphæra orbium segmenta AB, BC ex hypothesi sunt æqualia, et duobus partilibus triangulis ABD, CBD commune existit segmentum BD et AD basis basi CD æqualis, igitur per primum Menelai de sphæricis duo anguli ADB, BDC sunt æquales, et uterque eorum per definitionem rectus. Eodem quoque modo patet, duos angulos ABD, DBC esse æquales. Et quia, ut in libro secundo fuerat ostensum, ratio recti sinus segmenti BC ad segmenti CD rectum sinum est, sicut ratio sinus totius ad rectum sinum anguli CBD seu æqualis ABD, et per hypothesim in hac proportione priores termini dantur, ergo et quartus, rectus videlicet sinus anguli CBD, datur. Quare per tabulas rectorum sinuum angulus CBD datur; ex hipothesi igitur totus ABC angulus datus est. Dati ergo trianguli sphærici trium datorum laterum, et reliqua ut supra; quod oportuit demonstrare. Propositio quinta.Si vero alterum duorum segmentorum, quæ propositum ad B continent angulum, maius fuerit complemento circumferentiæ AB.
His itaque dispositis, si circumferentia propositum ad B angulum subtendens quadrante minor extiterit, ergo parallela ipsius IM sinus recti æqualis recto sinui complementi circumferentiæ ad B propositum angulum subtendentis cadet inter K signum et IM rectum sinum segmenti EFI. Sitque talis parallela NO; et productis IM et NO in partes M, O, donec occurrant ipsi HL, IM quidem in P, NO autem super Q. Igitur, ut prius, erit ratio ipsius INH ad HN sicut IMP ad NOQ. Et sicut est IH ad HN, sic fiat FD ad DR, Et dimidia ipsius IMP sit IS. Igitur, ut prius ostensum fuit, ex æquali erit ratio ipsius IS ad NOQ sicut ratio ipsius FG ad DR. In hac autem proportione priores tres termini dati sunt; ergo et quartus terminus DB datus erit. Nam IS dimidium est ipsius IMP datæ, quæ componitur ex recto sinu IM segmenti EFI dati per constructionem et MP æquali recto sinui segmenti CH similiter dati. Pari ratione NOQ recta probatur esse data. Et FG datur; est enim totus sinus ex hypothesi. Igitur BR recta datur, quæ est sinus versus seu sagitta propositi ad B anguli. Propositus ergo ad B angulus datur; quod oportuit demonstrare. Circumferentia deinde, quæ propositum ad B angulum subtendit, æquante quadrantem, igitur HK erit sinus versus circumferentiæ in parallelo HI, qua sublata ex semicirculo relinquitur circumferentia in eodem parallelo ad B angulo. Et super HL perpendicularis KA agatur; ergo iterum ratio ipsius IMP ad KA erit sicut IH ad HK. Et sicut IH ad HK sic fiat FB ad BT. Igitur, ut prius, ex æquali IS ad KA erit sicut FG ad DT. Est autem KA data; æqualis enim existit recto sinui segmenti CH per constructionem. In eadem ergo proportione datis tribus prioribus terminis et quartus terminus BT datur, sinus scilicet versus circumferentiæ circuli magni, qua sublata ex semicirculo relinquitur circumferentia æqualis ad B angulo proposito. Igitur propositus idem ad B angulus erit iterum datus. At circumferentia, quæ propositum ad B angulum subtendit, quadrantem superante, igitur per superius ostensa sinus versus subtendentis in parallelo HI circumferentiæ, qua dempta semicirculo eiusdem paralleli relinquitur circuinferentia similis proposito ad B angulo, erit minor quam HK recta. Sit itaque talis sinus versus HV; et per V ipsi IMP parallelus agatur XVY, secans dimetientem CGE super Z, et HL super Y. Et quia ratio ipsius IMP ad VY est sicut IH ad HV, sit igitur FD ad DZ sicut IH ad HV; ergo ex æquali IS ad VY erit sicut FG ad DZ. At huius proportionis tres termini priores dati sunt; ergo et quartus terminus videlicet DZ datus erit. Nam YV reliqua est, si VX detrahatur sinui recto segmenti GH. Est autem XV æqualis sinui recto circumferentiæ remanentis, si circumferentiæ ad B angulo subtensæ quadrans auferatur; ergo et VX datur; quare etiam VY dabitur. Et quoniam ratio ipsius IH ad HV est sicut FD ad DZ, ergo DZ datur, et erit sinus versus circumferentiæ magni circuli, qua dempta ex semicirculo eiusdem circuli magni relinquitur circumferentia æqualis proposito ad B angulo. Igitur idem propositus ad B angulus iterum datus erit; quod oportuit, ostendere.
Ex primo videlicet signo si dimetienti CGE parallelus agatur IBC, atque ad eam actis perpendicularibus duabus VXB, HC. Harum autem perpendicularium utraque datur. Nam VXB componitur ex VX per hypothesim data ex XB æquali recto sinui circumferentiæ EFI datæ. Et HC componitur ex eodem sinu circumferentiæ EFI recto et recto sinu segmenti HC. Igitur ut ante DZ versus sinus datus esse concluditur. Correlarium.Hinc etiam manifestum fit, quod in triangulo sphærico trium notorum laterum si propositimi angulum, quem datum efficere oporteat, duo continent segmenta, quorum utrumque quadrante minus, et maius borum duorum laterum excedat complementum minoris, et circumferentia eidem proposito angulo subtensa quadrante inferior extiterit, propositus angulus dabitur una proportione, habente in primo termino dimidium aggregati ex sinu recto segmenti compositi ex minore circa propositum angulum circumferentia cum complemento maioris circumferentiæ circa angulum eundem, atque eo segmento, quod relinquitur complemento eiusdem minoris circumferentiæ detracto maiori circumferentiæ circa eundem angulum, quod quidem segmentum discretionis et brevitatis gratia propositi anguli argumentum appellare duxi, atque eiusdem argumenti sinu recto; secundum terminum compositum ex sinu recto complementi circumferentiæ propositum subtendentis angulum atque sinu recto eiusdem argumenti; tertium terminum sinum totum; et quartum terminum sinum versum eius circumferentiæ, qua dempta ex semicirculo relinquitur circumferentia æqualis proposito angulo. Sin autem subtensa proposito angulo circumferentia quadrans extiterit, ergo propositus angulus rursum dabitur una proportione, quæ habet in primo dictum dimidium, secundum terminum sinum rectum eiusdem argumenti, tertium terminum sinum totum, et quartum terminum sinum versum eius circumferentiæ, qua detracta ex semicirculo circumferentia iterum relinquitur æqualis proposito angulo. Si vero circumferentia proposito subtensa angulo quadrante maior fuerit, idem angulus iterum dabitur unica proportione, quæ habeat eosdem terminos præter tertium, qui reliquus est, si quadrans subtensæ dicto angulo circumferentiæ detrahatur, et residui sinus rectus ex sinu recto memorati argumenti dematur, quod itaque hac sublatione remanserit tertius proportionis terminus erit. Propositio sexta.In sphærico triangulo trium datorum segmentorum propositum angulum circumferentia quadrante minore atque quadrante contentum datum efficere.
At circumferentia proposito subtensa ad B angulo quadrantem æquante, quod accidit, si quadrans circa B propositum angulum in communem G sectionem duorum CGE et DGF circulorum inciderit, et quia duæ AG, BG circumferentiæ quadrantes existunt, ergo in triangolo per librum primum ABG uterque duorum AB angulorum rectus est. Datus igitur est propositus ad B angulus.
Ergo in sphærico triangulo trium datorum segmentorum, et reliqua ut supra; quod oportuit demonstrare. Propositio septima.In sphærico triangulo trium datorum segmentorum angulum duobus contentum segmentis, quorum unum quadrante minus alterum quadrante maius, datum efficere.
Igitur segmenti AB circulus compleatur, sitque ille ABDE; punctumque D sit e diametro A signi, et E ex diametro signi B. Et per polos A, D descriptus sit circulus ACD; et per B, E polos circulus BCE. Et quia DE circumferentia æqualis est AB segmento, igitur DE circumferenlia minor est quadrante. Et quia BC segmentum per constructionem maius est quadrante, igitur reliquum de semicirculo CE segmentum quadrante inferius est. Esto deinde AC circumferentia angulo ABC subtensa quadrante minor, ergo et reliqua CD de semicirculo ACD quadrante maior est. In triangulo itaque sphærico CDE trium per constructionem datorum segmentorum, quorum duo DE, CE quadrante sunt minora, et tertium CD quadrante maius et subtensum angulo CED, idem angulus CED per prius ostensa dabitur; ergo de duobus rectis reliquus AEC datur. Igitiir suus æqualis ABC datus erit. Præterea ex ACD semicirculo quadrans auferatur ACF. Sitque per B, F, E semicirculus descriptus BFE. Et propositum esto in triangulo ABF trium datorum segmentorum AB, AF, BF angulum ABF datum efficere. Et quia in triangulo EFB per prius ostensa angulus DEF datur contentus duobus per constructionem datis segmentis BE, EF, cui quidam angulo quadrans BF subtenditur, ergo de duobus rectis reliquus ABF dabitur. Rursus ex semicirculo ACFD auferatur datum segmentum ACFG quadrante maius. Et per B, G, E signa semicirculus scribatur BGE; et sit BG segmentum quoque datum et quadrans maius. Propositumque sit angulum ABG notum datumque efficere. Et quoniam in triangulo ABG tria segmenta AB, AG et BG data sunt, et tria segmenta DE, DG et EG trianguli DEG data, et quodlibet eorum quadrante minus, ergo per prius ostensa angulus DEG datus erit; ergo et reliquus de duobus rectis ABG datus erit. In sphærico igitur triangulo trium datorum segmentorum angulum duobus contentum segmentis, quorum unum quadrante minus alterum quadrante maius, datum fecimus; quod oportuit efficere. Propositio octava.In sphærico triangulo trium datorum segmentorum angulum duobus contentum segmentis, quorum alterum quadrans alterum quadrante maius extiterit, datum constituere.
Duo igitur segmenta AB, BC agantur, donec in oppositum partem concurrant super D signo. Et quia utraque duarum circumferentiarum BAD et BCD semicirculus est, igitur segmentum AD quadrans erit, DC segmentum quadrante minus. Ergo per prius ostensa in triangulo ADC trium per hipothesim datorum segmentorum angulus ADC dabitur; ergo et suus æqualis ABC datus erit. Igitur in sphærico triangulo trium datorum segmentorum, et reliqua ut supra; quod oportuit efficere. Propositio nona.In sphærico triangulo trium datorum segmentorum angulum duobus contentum segmentis, utrisque quadrantem superantibus, datum notumque constituere.
Ergo per prius ostensa angulus ADC dabitur duobus AD, DC segmentis contentus, quorum utrumque quadrante inferius est; ergo et suus æqualis angulus ABC datur. In sphærico igitur triangulo, et reliqua ut supra; quod oportuit efficere. Propositio decima.In dato triangulo sphærico datis duobus segmentis datum angulum continentibus, quorum utrumque quadrante minus existat, maius quoque horum segmentorum inferius complemento alterius segmenti, tertium eiusdem trianguli segmentum, dato videlicet angulo subtensum, datum erit.
Igitur in sphærico triangulo datis duobus segmentis atque angulo ab eis contento, quorum quidem segmentorum utrumque quadrante inferius existat, atque longius eorundem segmentorum minus complemento brevioris segmenti, tertium eiusdem trianguli segmentum dato subtensum angulo dabitur; quod oportuit demonstrare. Lemma sive assumptum.At IQ dimidiam ipsius IK datam esse sic patet. Nam per constructionem tota IKL sinus rectus est segmenti EFI, quod datum est; nam ipsum componitur ex segmento EF æquali ipsi AB et FI complemento segmenti BH ex hipothesi dati. Est autem CH reliquum longiore circa datum ad B angulum segmento detracto ex complemento BC ipsius AB brevioris circa eundem ad B angulum segmenti. Igitur et sinus rectus IKL dato eidem subtensus segmento EFI datus est. Sed KL data est; æqualis enim recto sinui CH segmenti; igitur et reliqua IK recta datur; ergo et dimidia IQ data erit; quod oportuit perspicuum facere. Correlarium.Hinc manifestum erit, quod in triangulo sphærico, qualis proponitur, circumferentia dato subtensa angulo dabitur una proportione, quæ pro primo termino habeat sinum totum, pro secundo termino sinum versum eius circumferentiæ, qua ex semicirculo dempta relinquitur segmentum dato angulo æquale. Tertius terminus constituetur, si complementum longioris circa datum angulum segmenti breviori circa eundem angulum segmento adiiciatur; huius itaque aggregati sinui recto si sinus rectus differentiæ longioris segmenti et complementi brevioris iuxta eundem angulum segmenti dematur, remanentis rectæ dimidium tertius erit terminus. Quartus autem terminus erit quædam recta, cui si componatur eiusdem sinus rectus differentiæ, rectum conflabimus sinum complementi quæsitæ circumferentiæ, quæ dato subtenditur angulo. Propositio undecima.Si duo circa datum segmenta angulum æqualia fuerint, et utriusque complementum minus existat octava circuli magni, id est gradibus XLV minus, propositio hæc per præmissam fiet. Si vero idem complementum octavam magni partem circuli, id est gradus XLV, æquaverit aut superaverit, propositio hæc fit per sequentes propositiones. Aliter propositio hæc ostenditur.
Intelligatur itaque idem angulus ABC segmento BD bifariam divisus. Igitur uterque ad D angulus rectus est. Et quia in partili triangulo DBC habente duos datos angulos, videlicet CBD per constructionem acutum et BDC rectum, et oppositum eidem recto angulo segmentum BC quoque datum, igitur per secundum librum de triangulis sphæricis CD segmentum dato et acuto angulo CBD oppositum erit datum. Per præsentes autem hypotheses et primum librum Menelai in sphæricis CD segmentum æquale est ipsi AB segmento. Igitur totum segmentum AC dato ABC angulo subtensum datum erit. Ergo si in sphærico triangulo duo data et æqualis segmenta datum comprehendentia angulum, segmentum eidem dato subtensum angulo datum erit. Propositio XII.Si vero circa datum angulum B longius segmentum æquale fuerit complemento brevioris AB segmenti. Longius igitur idem segmentum, uti in subiecta figura, æquale erit BC segmento. Ergo a puncto C ipsi DGF parallelus agatur CH. Et segmenti EFH rectus sinus sit HI. Dato deinde ad B in parallelo per CH scripto similis circumferentiæ versus sinus sit HK. Et a puncto K ipsi HI recto sinui parallelus agatur KL. Et secundum rationem ipsius HK ad KC secetur BGF dimetiens in puncto M.
Ergo si circa datum angulum longius segmentum fuerit æquale complemento brevioris segmenti, circumferentia dato subtensa angulo data erit; quod oportuit demonstrare. Ista denique propositione propositio generaliter conficitur, quando alterum segmentum circa datum angulum æquale fuerit complemento alterius segmenti circa eundem angulum, si AB segmentum brevius extiterit sive longius altero. Correlarium.Inde etiam perspicuum fit, quod si datis duobus segmentis, quorum utrumque quadrante inferius extiterit, datum continentibus angulum alterum eorundem segmentorum æquale fuerit complemento alterius segmenti, datum eundem circumferentia subtendens angulum unica dabitur proportione, in qua primus terminus est sinus totus; secundus terminus sinus versus eius segmenti, quod detractum semicirculo relinquit segmentum æquale dato ad B angulo; tertius est dimidium sinus recti dupli alterius segmenti circa datum angulum, cuius quidem segmenti complementum æquale fuerit alteri segmento circa eundem angulum; quartus denique terminus sinus rectus complementi circumferentiæ, quæ datum subtendit angulum. Propositio XIII.Si denique circa datum angulum B longius segmentum exsuperaverit complementum alterius circa eundem angulum segmenti.
Sit autem primum angulus ad B datus quadrante inferior. Ergo signum O cadit inter I, K signa; et a signo ipsi KMN recto sinui parallelus agatur OPQ, secans dimetientem CGE super signo P et parallelam HL super Q signo. Et quia ex hypothesi ratio ipsius KH ad HO data est, igitur propter similes triangulos KHN, OHQ ratio KMN ad OPQ data erit. Est enim ratio ipsius KMN ad OPQ sicut ipsius KH ad HO. Et secundum rationem ipsius KO ad OH secetur DGF dimetiens super signo R. Erit igitur per constructionem FD ad DR sicut KMN ad OPQ. Secetur deinde KMN bifariam super S signo. Ex æquali igitur erit sicut FG ad DR sic KS ad OPQ. In hac autem proportione priores termini tres dati sunt. Est enim per constructionem FG sinus totus; DR sinus versus circumferentiæ, qua semicirculo sublata relinquitur circumferentia æqualis dato ad B angulo; KS quoque data; nam dimidium est ipsius rectæ KMN quæ componitur ex KM sinu recto dati segmenti EFK et sinu recto segmenti CH per constructionem quoque dati; ergo et KS data; igitur et quartus terminus, videlicet OPQ recta, datur. Et quia per constructionem PQ datur, ergo et reliqua OP data erit. Est autem OP sinus rectus complementi circumferentiæ, quæ dato ad B angulo subtenditur. Sin autem præmissæ proportionis quartus terminus æqualis fuerit sinui recto segmenti CH quemadmodum est ipsa IT, igitur circumferentia ad B angulo subtensa quadrans est. At ubi idem quartus terminus minor extiterit sinu recto eiusdem segmenti CH, velut est XY, erit itaque punctus X inter H, I puncta; et secundum rationem ipsius KH ad HX sit FGD ad DV. Et XY in partem X agatur, secans CGE dimetientem super puncto Z. Erit itaque perspicuum, circumferentiam dato ad B angulo subtensam maiorem esse quadrante, atque datam fieri unica proportione, in qua primus terminus est FG sinus totus; secundus terminus DV, sinus videlicet versus eius segmenti, quo ex semicirculo magni circuli sublato segmentum relinquitur æquale dato ad B angulo; tertius terminus KS per prius ostensa datus; et quartus terminus XY per eandem proportionem datus, quo dempto ex recta YZ, seu ex sinu recto segmenti CH, relinquitur XZ data, quæ æqualis est per constructionem sinui recto cuiusdam segmenti, quo addito ad quadrantem circumferentia magni conflabitur circuli, quæ datum ad B angulum subtendit. In spbærico igitur triangulo datis duobus segmentis datum continentibus angulum, quorum utrumque quadrante minus, longius vero exsuperet complementum alterius circa eundem angulum segmenti, tertium quoque in eodem triangulo segmentum datum erit. Correlarium.Hinc perspicuum est, quod in triangulo spbærico, qualis proponitur, dato angulo duobus contento datis segmentis, qualia proponuntur, subtensum segmentum unica datum sit proportione, in qua primus terminus est sinus totus; secundus terminus sinus versus eius circumferentiæ, qua semicirculo detracta segmentum relinquitur dato æquale angulo; tertius terminus efficietur, si circumferentiæ conflateæ ex breviore circa datum angulum segmento atque ex complemento longioris iuxta eundem angulum segmenti rectus sinus addatur recto sinui differentiæ eiusdem longioris et complementi brevioris circa eundem datum segmenti; nam horum sinuum aggregati dimidium tertins erit terminus; quartus terminus erit recta qnædam, qua superante rectum sinum prædictæ differentiæ, eodem sinu ex ea dempto relinquitur sinus rectus complementi circumferentiæ dato angulo subtensæ, quæ ex consequenti data erit. Si vero idem quartus terminus æquaverit prædictæ sinum rectum differentiæ, igitur circumferentia dato subtensa angulo quadrans erit. At eodem quarto termino existente minore quam sit rectus sinus eiusdem differentiæ, igitur idem quartus terminus, sublatus ex sæpius memoratæ differentiæ recto sinu, relinquit rectum sinum cuiusdam segmenti, quo ad quadrantem congregato circumferentia constituetur datum subtendens angulum. Propositio XIV.Dato angulo duobus datis comprehenso segmentis, quorum alterum quadrans sit, alterum vero minus quadrante, subtensum segmentum esse datum estendere.
Sit denique ABK datus angulus, quem segmentrun AB quadrante minus atque quadrans BK comprehendant, subtensumque ei segmentum AK, secans CGE magnum circulum super L signo. Et quia eiusdem magni circuli CGE polus est A signum, ergo in triangulo GKL angulus GLK rectus est, atque angulus KGL datus — æqualis enim per constructionem dato AB segmento —, atque segmentum GK etiam datum, quia subtractum ex segmento dato KF seu angulo ABK relinquit quadrantem; igitur segmentum KL eidem acuto angulo KGL obtensum datum existit. Datur autem segmentum ALK nam per constructionem quadrans est. Ergo totum segmentum ALK datum erit, quod dato ABK angulo subtenditur. Ergo dato angulo duobus datis comprehenso segmentis, quorum alterum quadrans alterum quadrante minus existat, subtensum quoque eidem angulo segmentum datum est; q. o. d. Propositio XV.In sphærico triangulo duobus datis segmentis datum continentibus angulum, quorum alterum quadrante minus, alterum quadrante maius, circumferentia eidem dato subtensa angulo data erit. Sit ergo super sphærica superficie datus triangulus ABC duo data possidens segmenta AB, BC datum angulum ABC continentia, quorum alterum AB sit quadrante minus, alterum vero BC quadrante maius. Et propositum esto circumferentiam AC dato angulo ABC subtensam datam ostendere.
Ergo in sphærico triangulo, etc.; q. o. d. Propositio XVI.In sphærica superficie duobus datis segmentis datum continentibus angulum, quorum alterum quadrans alterum quadrante maius extiterit, circumferentia eidem dato subtensa angulo dabitur.
Producantur duo segmenta AB, BC, donec in partem A, C concurrant super D puncto. Et quoniam BAD circumferentia semicirculus est, et AB segmentum quadrans, ergo et reliquum segmentum AD quadrans erit. Rursus quia circumferentia BCD semicirculus est, et BC segmentum quadrante maius atque datum, ergo reliquum segmentum CD quadrante minus erit atque datum. Est autem angulus ADC æqualis angulo ABC dato per constructionem. Ergo per decimam quartam propositionem circumferentia AC dato angulo ADC subtensa data erit. In sphærica igitur superficie duobus datis segmentis AB, BC datum angulum ABC continentibus, quorum alterum quadrans alterum quadrante maius existat, circumferentia AC eundem subtendens angulum ABC data est; q. o. d. Propositio XVII.In sphærica quapiam superficie datis duobus segmentis datum continentibus angulum, quorum utrumque quadrante maius existat, circumferentia eidem dato subtensa angulo data erit.
Et quoniam manente proxima figura utraque duarum circumferentiarum BAD et BCD semicirculus est, et utrumque duorum segmentorum AB, BC quadrante maius atque datum ex hipothesi, ergo reliqua duo segmenta AD, DC data sunt, et utrumque minus quadrante; et angulus ab eis comprehensus ADC datus — æqualis enim per constructionem ABC dato angulo —, igitur aut per X vel XI aut XII vel etiam XIII propositionem circumferentia AC dato subtensa angulo ABC data erit. In sphærica igitur quapiam superficie duobus datis, etc.; quod o. ostendere. Correlarium generale cuilibet propositioni huius libri serviens.Perspicuum etiam est, quodlibet præceptum huius libri confici posse unica tantum vel divisionis aut multiplicationis operatione, floccipensis numerorum additionibus et subtractionnibus, quibus in eisdem propositionibus nonnunquam opus erit, quoniam ipsæ additiones et subtractiones nullo pæne fiunt negotio, tabulis videlicet rectorum habitis sinuum, in quibus maximus sinus rectus subiicitur partium 10000000. | |||||
|
|||||
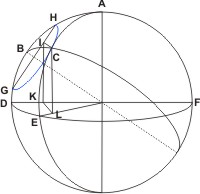 In dato igitur sphærico triangulo ABC duo segmenta AB, BC, quorum utrumque quadrante sit minus, propositum angulum ABC comprehendant; et circulus ipsius AB segmenti sit ABD; atque complementum AC segmenti angulum ABC subtendentis sit CE. Et super A quidem polo spatio autem AE magnus describatur circulus DEF, secans circulum ABD super D, F signis. Rursus super B polo intervallo autem BC parvus scribatur circulus GCH, secans eundem circulum ABD super G, H signis. Per constructionem autem CH circumferentia similis est angulo ABC proposito, cuius quidem circumferentiæ sinus versus sit HI, a cuius termino I perpendicularis IK ad planum circuli DEF agatur; et sinus rectus ipsius CE segmenti sit CL. Dico, quod perpendicularis IK sit æqualis recto sinui CL.
In dato igitur sphærico triangulo ABC duo segmenta AB, BC, quorum utrumque quadrante sit minus, propositum angulum ABC comprehendant; et circulus ipsius AB segmenti sit ABD; atque complementum AC segmenti angulum ABC subtendentis sit CE. Et super A quidem polo spatio autem AE magnus describatur circulus DEF, secans circulum ABD super D, F signis. Rursus super B polo intervallo autem BC parvus scribatur circulus GCH, secans eundem circulum ABD super G, H signis. Per constructionem autem CH circumferentia similis est angulo ABC proposito, cuius quidem circumferentiæ sinus versus sit HI, a cuius termino I perpendicularis IK ad planum circuli DEF agatur; et sinus rectus ipsius CE segmenti sit CL. Dico, quod perpendicularis IK sit æqualis recto sinui CL.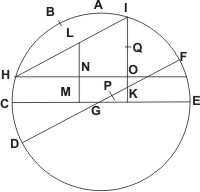 Et quia per constructionem duæ rectæ lineæ IK et LM sunt parallelæ, igitur per XXIX propositionem libri primi elementorum anguli ad N, O signa sunt æquales, videlicet angulus HNL æqualis angulo NOI; uterque enim rectus. Et quoniam duobus triangulis IHO, LHN communis angulus est NHL, igitur duo trianguli IHO, LHN sunt æquianguli et similes. Ergo per propositionem quartam libri sexti elementorum ratio ipsius ILH ad HL datur; est enim sicut IO ad LN ratio data. Et quia IH magnitudine datur — est enim dimetiens paralleli super B polo et secundum BH datam sectionem descripti —, igitur et HL, item et reliqua IL magnitudine datur. Est autem IL per ea, quæ prius ostensa sunt, sinus versus circumferentiæ in parallelo IH similis angulo proposito, quem datum oportebat efficere.
Et quia per constructionem duæ rectæ lineæ IK et LM sunt parallelæ, igitur per XXIX propositionem libri primi elementorum anguli ad N, O signa sunt æquales, videlicet angulus HNL æqualis angulo NOI; uterque enim rectus. Et quoniam duobus triangulis IHO, LHN communis angulus est NHL, igitur duo trianguli IHO, LHN sunt æquianguli et similes. Ergo per propositionem quartam libri sexti elementorum ratio ipsius ILH ad HL datur; est enim sicut IO ad LN ratio data. Et quia IH magnitudine datur — est enim dimetiens paralleli super B polo et secundum BH datam sectionem descripti —, igitur et HL, item et reliqua IL magnitudine datur. Est autem IL per ea, quæ prius ostensa sunt, sinus versus circumferentiæ in parallelo IH similis angulo proposito, quem datum oportebat efficere.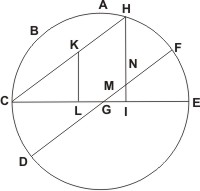 Igitur ex C puncto ipsi DGF parallelus agatur CH, secans circulum ABCDE ad H signum. Et super CGE dimetientem perpendicularis agatur HI. Et complementi circumferentiæ subtendentis ad B angulum propositum sit KL sinus.
Igitur ex C puncto ipsi DGF parallelus agatur CH, secans circulum ABCDE ad H signum. Et super CGE dimetientem perpendicularis agatur HI. Et complementi circumferentiæ subtendentis ad B angulum propositum sit KL sinus.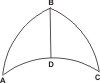 In dato igitur sphærico triangulo ABC trium datorum laterum, habente duo latera AB, BC æqualia, propositum sit angulum ABC datum efficere.
In dato igitur sphærico triangulo ABC trium datorum laterum, habente duo latera AB, BC æqualia, propositum sit angulum ABC datum efficere.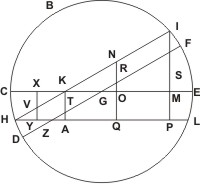 Quod quidem complementum existit BC circumferentia, sitque illud æquale BCH segmento; itaque H punctus cadet inter C, D signa. Et ab H signo ipsi DGF dimetienti parallelus HKI agatur, secans dimetientem CGE super K signo. Rursus ipsi CGE dimetienti parallelus agatur HL. Et circumferentiæ EFI sinus rectus sit IM.
Quod quidem complementum existit BC circumferentia, sitque illud æquale BCH segmento; itaque H punctus cadet inter C, D signa. Et ab H signo ipsi DGF dimetienti parallelus HKI agatur, secans dimetientem CGE super K signo. Rursus ipsi CGE dimetienti parallelus agatur HL. Et circumferentiæ EFI sinus rectus sit IM.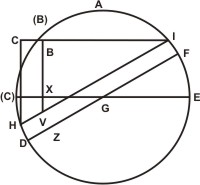 Hæc tertia particula huius quintæ propositionis aliter fieri poterit,
Hæc tertia particula huius quintæ propositionis aliter fieri poterit,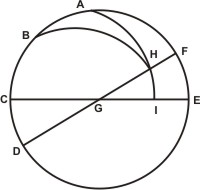 Sit igitur eadem circumferentia minor quadrante AB, cuius circulus ABCBEF. Et supra A polo circulus magnus descriptus sit CGE. Rursus super polo B descriptus magnus circulus sit DGF. Et esto inprimis circumferentia proposito ad B angulo subtensa AH quadrante minor, quæ agatur in partem H, donec secat circulum CGE super I signo.
Sit igitur eadem circumferentia minor quadrante AB, cuius circulus ABCBEF. Et supra A polo circulus magnus descriptus sit CGE. Rursus super polo B descriptus magnus circulus sit DGF. Et esto inprimis circumferentia proposito ad B angulo subtensa AH quadrante minor, quæ agatur in partem H, donec secat circulum CGE super I signo.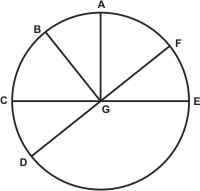 Et quia circuli CGE per constructionem polus est A signum, igitur anguli ad I recti sunt. Et quia in sphærico triangulo GHI rectangulo angulus HGI datus est — eius enim magnitudo circumferential FE data, æqualis namque ipsi AB segmento —, igitur per secundum librum HG segmentum recto angulo GIH oppositum datur; ergo et eius complementum FH datur, quod magnitudo existit propositi ABH anguli. Datus igitur est propositus ad B angulus.
Et quia circuli CGE per constructionem polus est A signum, igitur anguli ad I recti sunt. Et quia in sphærico triangulo GHI rectangulo angulus HGI datus est — eius enim magnitudo circumferential FE data, æqualis namque ipsi AB segmento —, igitur per secundum librum HG segmentum recto angulo GIH oppositum datur; ergo et eius complementum FH datur, quod magnitudo existit propositi ABH anguli. Datus igitur est propositus ad B angulus.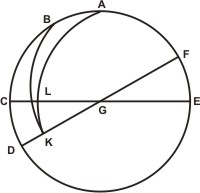 Sit denique circumferentia ad B subtensa angulo maior quadrante. Sitque ipsa AK secans circulum CGE super L signo. Rursus quia in triangulo GKL angulus ad L rectus est, et acutus angulus KGL datus — æqualis enim circumferentiæ CD datæ, quæ æqualis est ipsi AB segmento —, et LK segmentum dato angulo KGL subtensum datus — relinquitur enim, si quadrans AL dematur dato segmento ALK —, igitur per ea, quæ ostensa fuerunt in libro secundo, segmentum GK datum, quod cum quadrante FG æquale est proposito ad B angulo. Igitur idem ad B angulus datur.
Sit denique circumferentia ad B subtensa angulo maior quadrante. Sitque ipsa AK secans circulum CGE super L signo. Rursus quia in triangulo GKL angulus ad L rectus est, et acutus angulus KGL datus — æqualis enim circumferentiæ CD datæ, quæ æqualis est ipsi AB segmento —, et LK segmentum dato angulo KGL subtensum datus — relinquitur enim, si quadrans AL dematur dato segmento ALK —, igitur per ea, quæ ostensa fuerunt in libro secundo, segmentum GK datum, quod cum quadrante FG æquale est proposito ad B angulo. Igitur idem ad B angulus datur.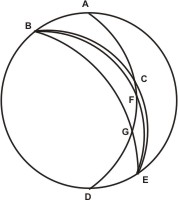 Sit ergo sphæricus triangulus ABC trium datorum segmentorum AB, BC, CA; et esto propositum angulum ABC datum efficere contentum duobus segmentis AB et BC datis, AB quidem minore quam sit quadrans, BC vero quadrantem superante.
Sit ergo sphæricus triangulus ABC trium datorum segmentorum AB, BC, CA; et esto propositum angulum ABC datum efficere contentum duobus segmentis AB et BC datis, AB quidem minore quam sit quadrans, BC vero quadrantem superante.
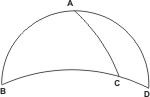 In triangulo itaque ABC trium datorum segmentorum propositum sit angulum ABC datum efficere, AB quadrante, et BC segmento quadrantem superante.
In triangulo itaque ABC trium datorum segmentorum propositum sit angulum ABC datum efficere, AB quadrante, et BC segmento quadrantem superante.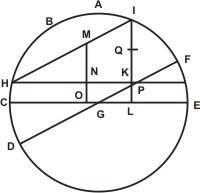 Sit itaque in dato triangulo minus duorum segmentorum AB, datusque angulus ad B signum, perficiaturque ipsius AB segmenti circulus, qui sit ABCBEF. Et super A polo magni circuli scripti sit dimetiens CGE; et super B polo circuli magni diameter sit DGF; et maius segmentum circa datum angulum sit minus complemento segmenti AB, æquale videlicet segmento BH. Et a puncto H ipsis CGE et DGF diametris duæ parallelæ agantur HI, HK, HI quidem ipsi BF, HK vero ipsi CGE dimetienti. Atque segmenti EFI rectus sinus sit IKL, secans parallelam HK in puncto K, Et in parallelo per IH scripto sit IM sinus versus eius segmenti, quod simile est dato ad B angulo; atque ab M signo super CGE dimetientem perpendicularis agatur MNO, secans parallelam HK super N signo. Erit itaque per ea, quæ prius ostensa fuerunt, MNO perpendicularis æqualis recto sinui complementi circumferentiæ dato ad B angulo subtensæ. Et quia duo triangula IHK et MHN sunt similis, igitur ratio ipsius IK ad MN est sicut IH ad HM. Est autem ratio ipsius IH ad HM data; ex hipothesi namque est sicut dimetiens magni circuli ad sinum versum eius circumferentiæ eiusdem magni circuli, qua quidem circumferentia deducta semicirculo relinquitur segmentum dato ad B angulo subtensum. Fiat igitur FD dimetiens ad DP sicut IH ad HM aut sicut IK ad MN; et divisa IK bifariam in puncto Q erit igitur ex æquali ratio ipsius GF semidiametri orbis AB ad DP sicut IQ ad MN. In hac autem proportione prioribus terminis tribus datis dabitur et quartus terminus MN. Data quoque existit NO; nam ipsa æqualis est recto sinui dati segmenti HC quod ex hipothesi differentia est Inter maius ad B angulum segmentum et inter complementum segmenti AB. Et quia tota MNO datur, ergo et reliqua MN; quia per constructionem recta MNO æqualis est recto sinui complementi circumferentiæ dato subtensæ ad B angulo.
Sit itaque in dato triangulo minus duorum segmentorum AB, datusque angulus ad B signum, perficiaturque ipsius AB segmenti circulus, qui sit ABCBEF. Et super A polo magni circuli scripti sit dimetiens CGE; et super B polo circuli magni diameter sit DGF; et maius segmentum circa datum angulum sit minus complemento segmenti AB, æquale videlicet segmento BH. Et a puncto H ipsis CGE et DGF diametris duæ parallelæ agantur HI, HK, HI quidem ipsi BF, HK vero ipsi CGE dimetienti. Atque segmenti EFI rectus sinus sit IKL, secans parallelam HK in puncto K, Et in parallelo per IH scripto sit IM sinus versus eius segmenti, quod simile est dato ad B angulo; atque ab M signo super CGE dimetientem perpendicularis agatur MNO, secans parallelam HK super N signo. Erit itaque per ea, quæ prius ostensa fuerunt, MNO perpendicularis æqualis recto sinui complementi circumferentiæ dato ad B angulo subtensæ. Et quia duo triangula IHK et MHN sunt similis, igitur ratio ipsius IK ad MN est sicut IH ad HM. Est autem ratio ipsius IH ad HM data; ex hipothesi namque est sicut dimetiens magni circuli ad sinum versum eius circumferentiæ eiusdem magni circuli, qua quidem circumferentia deducta semicirculo relinquitur segmentum dato ad B angulo subtensum. Fiat igitur FD dimetiens ad DP sicut IH ad HM aut sicut IK ad MN; et divisa IK bifariam in puncto Q erit igitur ex æquali ratio ipsius GF semidiametri orbis AB ad DP sicut IQ ad MN. In hac autem proportione prioribus terminis tribus datis dabitur et quartus terminus MN. Data quoque existit NO; nam ipsa æqualis est recto sinui dati segmenti HC quod ex hipothesi differentia est Inter maius ad B angulum segmentum et inter complementum segmenti AB. Et quia tota MNO datur, ergo et reliqua MN; quia per constructionem recta MNO æqualis est recto sinui complementi circumferentiæ dato subtensæ ad B angulo.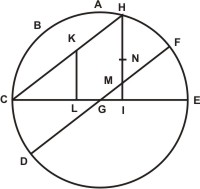 Et quia duo trianguK HCI et CKL similes sunt, ergo ratio ipsius HC ad CK, seu ipsius FD ad DM, est sicut HI ad KL. Ipsa deinde HI bifariam secetur super N signo; igitur ex æquali ratio ipsius FG ad DM erit sicut HN ad KL. In hac autem proportione priores termini tres dantur. Est enim FG sinus totus per diffinitionem; DM vero versus sinus eius segmenti, quo dempto ex semicirculo segmentum relinquitur æquale dato ad B angulo; HN denique dimidium ipsius HI recti sinus segmenti EFH per constructionem similiter dati — nam ipsum duplum AB dati segmenti —, ergo et quartus terminus KL datur. Est autem KL æqualis recto sinui complementi circumferentiæ, quæ in subiecto triangulo datum ad B angulum subtenditur.
Et quia duo trianguK HCI et CKL similes sunt, ergo ratio ipsius HC ad CK, seu ipsius FD ad DM, est sicut HI ad KL. Ipsa deinde HI bifariam secetur super N signo; igitur ex æquali ratio ipsius FG ad DM erit sicut HN ad KL. In hac autem proportione priores termini tres dantur. Est enim FG sinus totus per diffinitionem; DM vero versus sinus eius segmenti, quo dempto ex semicirculo segmentum relinquitur æquale dato ad B angulo; HN denique dimidium ipsius HI recti sinus segmenti EFH per constructionem similiter dati — nam ipsum duplum AB dati segmenti —, ergo et quartus terminus KL datur. Est autem KL æqualis recto sinui complementi circumferentiæ, quæ in subiecto triangulo datum ad B angulum subtenditur.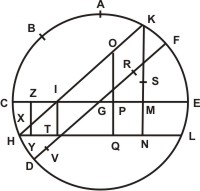 Igitur, ut prius, descriptus esto circulus ABCDEF duoque dimetientes CGE et DGF. Et longius duorum segmentorum datum ad B angulum comprehendentium sit æquale BH segmento; et quia ex hypothesi idem segmen|tum exsuperat complementum segmenti AB, ideo H punctus cadit inter C, D signa. Deinde a signo H dimetienti DGF parallelus agatur HIK, secans CGE dimetientem super I signo et circumferentiam ABCDEF super K puncto. Rursus ipsi CGE dimetienti ab eodem signo H parallelus agatur HL. Et circumferentiæ EFK sinus rectus sit KM, qui producatur in partem M, donec secet HL super N signo. Et sit KO sinus versus circumferentiæ in parallelo HK similis angulo ad B signum dato.
Igitur, ut prius, descriptus esto circulus ABCDEF duoque dimetientes CGE et DGF. Et longius duorum segmentorum datum ad B angulum comprehendentium sit æquale BH segmento; et quia ex hypothesi idem segmen|tum exsuperat complementum segmenti AB, ideo H punctus cadit inter C, D signa. Deinde a signo H dimetienti DGF parallelus agatur HIK, secans CGE dimetientem super I signo et circumferentiam ABCDEF super K puncto. Rursus ipsi CGE dimetienti ab eodem signo H parallelus agatur HL. Et circumferentiæ EFK sinus rectus sit KM, qui producatur in partem M, donec secet HL super N signo. Et sit KO sinus versus circumferentiæ in parallelo HK similis angulo ad B signum dato.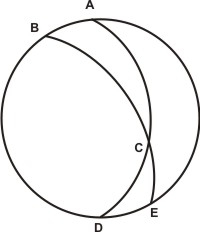 Segmenti igitur AB drculus sit ABDE; et producatur circumferentia AC in partem C, donec eundem circulum ABDE secet super D. Similiter BC in partem C producatur, quousque circulum ABDE etiam secet super E signo. Et quia per constructionem BCE semicirculus est, et per hipothesim BC segmentum quadrante maius atque magnitudine datum, igitur reliquum segmentum CE quadrante minus erit atque magnitudine datum. Et quia DE segmentum per constructionem æquale est ipsi AB segmento, quod ex hipothesi quadrante minus atque datum est, ergo æquale segmentum DE quadrante minus atque datum existit. Et quoniam per constructionem angulus AEC datus existit — æqualis enim dato angulo ABC —, igitur de duobus rectis angulis reliquus CED datus. Et quia, velut patuit, duo segmenta DE, CE circa eundem datum angulum CED data sunt, atque utrumque quadrante minus, ergo per præcedentes propositiones segmentum CD dato CED angolo subtensum datum erit, quo ex semicirculo ACD sublato segmentum AC dato subtensum angulo ABC datum quoque relinquitur.
Segmenti igitur AB drculus sit ABDE; et producatur circumferentia AC in partem C, donec eundem circulum ABDE secet super D. Similiter BC in partem C producatur, quousque circulum ABDE etiam secet super E signo. Et quia per constructionem BCE semicirculus est, et per hipothesim BC segmentum quadrante maius atque magnitudine datum, igitur reliquum segmentum CE quadrante minus erit atque magnitudine datum. Et quia DE segmentum per constructionem æquale est ipsi AB segmento, quod ex hipothesi quadrante minus atque datum est, ergo æquale segmentum DE quadrante minus atque datum existit. Et quoniam per constructionem angulus AEC datus existit — æqualis enim dato angulo ABC —, igitur de duobus rectis angulis reliquus CED datus. Et quia, velut patuit, duo segmenta DE, CE circa eundem datum angulum CED data sunt, atque utrumque quadrante minus, ergo per præcedentes propositiones segmentum CD dato CED angolo subtensum datum erit, quo ex semicirculo ACD sublato segmentum AC dato subtensum angulo ABC datum quoque relinquitur.