Wie kam der Nürnberger Johannis Werner auf die Prosthaphaerese?

Axel Anthon Björnbo führt die Prosthapaerese auf Johannes Werner zurück. Die erste pro­stha­phae­retische Gleichung soll implizit in den Lehrsätzen 2 bis 5 des 4. Buches De Triangulis Sphæricis ent­halten sein.

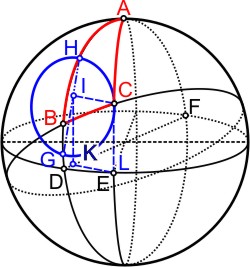Die Abbildung des ersten Lehrsatzes habe ich um­ge­zeichnet um die räumlichen Verhältnisse etwas klarer zu machen. Werner gibt ein sphärisches Dreieck ABC vor. Die Ecken liegen auf Großkreisen innerhalb eines Quadranten der Kugel. Um die Ecke B schlägt er einen Kleinkreis der durch die Ecke C geht (Radius r = BC). Damit bereitet er die Projektion des sphärischen Drei­ecks in die Ebene des Großkreises ABDG vor (siehe auch grafische Lösung der Aufgaben im sphärischen Dreieck), die er im zweiten und den fol­gen­den Lehr­sät­zen verwendet.

Nun konstruiert Werner das Rechteck CIKL und be­gründet seine Argumente mit den Lehrsätzen aus Euklids Elementa. In der Ebene des blauen Klein­kreises liegt der Durchmesser GH, der die Schnitt­punkte mit dem Groß­kreis ABD verbindet, auf dem die eine Seite des sphärischen Dreiecks ABC liegt. Die Ver­bin­dungs­linie CI steht senkrecht auf dem Durch­mes­ser GH. Und da die Dreiecksecke B der Pol zum blauen Kleinkreis ist (sie liegt senkrecht über dem Mit­tel­punkt), bildet sich der sphärische Winkel ∠ABC auch in der Kreisebene ab. Damit ist CI der Sinus und HI der Sinus versus des Winkels ∠ABC (zur Nomenklatur siehe Sinustabellen). Das Lot CL ist der Sinus des Großkreisbogens CE, und CE das Komplement zur Dreiecksseite AC.

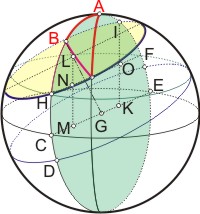Im zweiten Lehrsatz verwendet Werner die Projektion des sphärischen Dreiecks in die Ebene eines Großkreises, auf dem eine der Dreiecksseiten liegt. (Leider wechselt er auch die Be­zeich­nung der Punkte. In der perspektivischen Ansicht liegen alle mit Buchstaben benannten Punkte in der grünen Groß­kreis­ebene.) Dieser Großkreis der Seite AB (rot) ist die Pro­jek­tions­fläche, und BH (lila) ist die Dreiecksseite BC aus der ersten Ab­bil­dung. Der blaue Kleinkreis aus der ersten Ab­bil­dung ist nun HLI. Der Mittelpunkt des Kleinkreises ist nun der Punkt L, von dem aus das Lot LNM auf den Durchmesser CGE gefällt wird. Von I, dem Schnittpunkt des Kleinkreises mit den pro­ji­zierten Groß­kreis, wird ebenfalls ein Lot IOK gefällt. Die Spur der Ebene des Großkreises, auf dem die Seite BC liegt ist der Durch­messer DGF. Er schneidet den Großkreis CE im Punkte P, der gleich­zeitig der Mittelpunkt der Kugel ist, und das Lot IOK in K. Dessen Abschnitt IK ist der Sinus des Kreisbogens IFE. Das Lot LM ist der Sinus des Komplements der dritten Dreiecksseite AC (s. Lehrsatz 1).

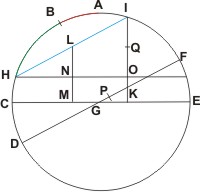Durch die beiden Lote entstehen zwei rechtwinklige Dreiecke LHN und IHO, die den Winel ∠LHN gemeinsam haben. Sie sind damit ähnlich sind (sie stimmen in zwei Winkeln, dem ∠LHN und dem rechten ∠LNH, überein). Nun verhalten sich die Strecken HI zu HL wie IO zu LN nach dem Strahlensatz des Euclid (Ele­men­ta, Liber VI, Propositio 2). Die Strecke HI ist der Sinus versus des Winkels ∠ABC im gegebenen sphärischen Dreieck (s. o.) und HL ist der Sinus des Bogens BH. Damit kann man IL = HI - HL = sin versus IBH berechnen.

Im Hilfssatz (Lemma) ergänzt er dass IO und LN parallel sind. Weil IK der Sinus des Bogens IEF ist, ist der Bogen EF gleich dem Bo­gen AB, und FI gleich DH, dem Komplement von BH (B ist der Pol des Groß­kreises DFG!). Damit kann man die Strecke IK be­rech­nen, und mit dem Strahlensatz auch LM. Außerdem sind OK und NM bekannt: sie sind der Sinus rectus des Bogens HC, der wie­derum das Komplement des Bogens ABH ist. Wenn man von IK und LM jeweils OK oder MN abzieht, er­hält man die verbleibenden Strecken IO und LN.

Damit folgt (Correlarium):

Quellen

1. Axel Anthon Björnbo (Herausg.), Ioannis Verneri De Triangulis Sphæricis, Libri Quatuor. Abhandlungen zur Geschichte der Mathematischen Wissenschaften, Heft XXIV. Leipzig 1907.
2. Dr. A. von Braunmühl: Vorleseungen über die Geschichte der Trigonometrie. Erster Teil. Leipzig 1900.