Joannis Verneri Norimbergensis
De Triangulis Sphaericis

Die Prosthaphaerese wird Johannes Werner aus Nürnberg zugeschrieben. Er soll sie um 1510 in einer Handschrift dargestellt haben. Da aber keine Druckwerke von ihm überliefert sind, ist die Quellenlage dürftig.

Eine Ausgabe der vier Bücher über sphärische Dreiecke ist in der kommentierten Ausgabe von Axel Anthon Björnbo enthalten Teubner Verlag Leipzig 1907). Björbo schreibt zur Herkunft der Texte im Anhang:

3. Herausgeberbemerkungen.

Die vorliegende Textausgabe beruht auf einer einzigen Handschrift, dem Codex Reginensis latinus 1259, d. h. Nr. 1259 der Regina Sveciae-Sammlung der Vatikanischen Bibliothek zu Rom. In dem handschriftlichen Katalog über diese von Gustaf Adolfs Tochter, Königin Christina von Schweden, der pästlichen Bibliothek geschenkte Sammlung hat die Handschrift folgende Bezeichnung: "Nr. 1259. Joannis Verneri Norimbergensis de triangulis sphaericis libri IV. Cod. ex papyro 4to, anno 1495." Die Handschrift ist aus Papier von einer recht dünnen und durchsichtigen Qualität; sie ist in klein Quarto mit ca. 21x16 cm Blattfläche und besteht aus 495 oben rechts numerierten und mehreren (leeren) unnumerierten Blättern. Der ganze Text ist von einer Hand geschrieben, dem Anschein nach der eines professionellen Schönschreibers aus dem Anfang des 16. Jahrhunderts. Die von dieser Hand angebrachten Kustoden und Bogennummem (Buchstaben) zeigen, daß die Handschrift vollständig ist, und daß die leeren unnumerierten Blätter für spätere Eintragungen bestimmt waren und also Textlücken bedeuten. Damit paßt es auch, daß die Foliierung von neuerer Hand herstammt. Am breiten Rande kommen außer Textkorrekturen der ersten Hand kritische Randnoten einer zweiten gleichzeitigen Hand vor, die offenbar keinem Schönschreiber gehört. Randnoten und Textkorrekturen von ein paar jüngeren Händen findet man auch; sie sind aber sehr selten. Figuren fehlen ganz und ebenso Datierungen, so daß die in dem alten handschriftlichen Katalog angeführte Jahreszahl 1495 keinen Anknüpfungspunkt im Texte hat.

Björbo bezieht sich auf die Propositiones 2 bis 5 aus werners viertem Buch. Die sind hier zitiert:

Liber Quartus.

Propositio prima.

In dato sphaerico triangulo duobus segmentis, quorum utrumque fuerit quadrante minus, propositum aliquem comprehendentibus angulum, si super [termino] unius eorundem segmentorum tanquam polo magnus scribatur circulus, et super altero quidem eiusdem segmenti termino, spatio autem alterius duorum iuxta eundem angulum segmentorum parvus describatur circulus, ex quo circumferentia proposito angulo similis auferatur, et a termino sinus versi eandem subtendentis circumferentiam perpendicularis ad magni circuli planum deducatur, erit eadem perpendicularis aequalis sinui recto complementi eius segmenti, quod in dato triangulo eundem propositum subtendit angulum.

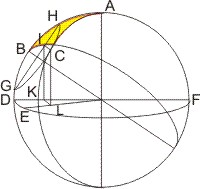Skizze In dato igitur sphaerico triangulo ABC duo segmenta AB, BC, quorum utrumque quadrante sit minus, propositum angulum ABC comprehendant; et circulus ipsius AB segmenti sit ABD; atque complementum AC segmenti angulum ABC subtendentis sit CE. Et super A quidem polo spatio autem AE magnus describatur circulus DEF, secans circulum ABD super D, F signis. Rursus super B polo intervallo autem BC parvus scribatur circulus GCH, secans eundem circulum ABD super G, H signis. Per constructionem autem CH circumferentia similis est angulo ABC proposito, cuius quidem circumferentiae sinus versus sit HI, a cuius termino I perpendicularis IK ad planum circuli DEF agatur; et sinus rectus ipsius CE segmenti sit CL. Dico, quod perpendicularis IK sit aequalis recto sinui CL.

Coniunctis itaque CI, LK rectis, et quia planum quadrantis ACE erectum est ad planum circuli DEF, igitur rectus sinus CL ad idem planum circuli DEF erigitur; nam rectus sinus CL perpendicularis est ad communem sectionem duorum planorum, quadrantis videlicet ACE et magni circuli DEF. Est autem IK per constructionem ad idem planum DEF perpendicularis; ergo perpendicularis IK et sinus rectus CL sunt paralleli per propositionem sextam libri undecima elementorum Euclidis. Et quia per diffinitionem [II, def. 2] CI rectus est sinus segmenti HC, et planum parvi circuli GCH erectum est plano circuli ABD, igitur duorum angulorum CIK et IKL uterque rectus per tertiam diffinitionem eiusdem libri undecimi; nam HI pars est communis sectionis duorum planorum circuli magni ABD et circuli parvi GCH. Et quia utraque rectarum linearum CI, KL in eodem sunt plano IK, CL rectarum linearum per septimam propositionem eiusdem libri undecimi, igitur per XXVIII libri primi eorundem elementorum duse rectae CI, KL sunt parallelae. Igitur quadrilaterum CIKL est parallelogrammum. Ergo IK perpendicularis aequalis est sinui recto CL; nam per XXXIV propositionem primi libri eorundem elementarum "parallelogramorum locorum latera, quae ex opposito, et anguli, aequalia sunt adinvicem".

Igitur in dato sphaerico triangulo duobus segmentis, etc.; quod oportuit demonstrare.

Propositio secunda.

Datis tribus lateribus propositi trianguli sphaerici angulum datum efficere duobus contentum segmentis, quorum utrumque quadrante minus extiterit.

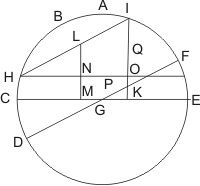Skizze Sit ergo alterum segmentorum, quae propositum continent angulum, AB; atque maximus circulus, cuius segmentum AB portio existit, sit ABCDEF. Et descripti super B polo maximi circuli dimetiens sit DF, atque super B polo maximi descripti circuli dimetiens sit DF. Hi duo dimetientes se invicem secabunt in centro sphaerae, quod sit G. Sit autem reliquum segmentorum, a quibus propositus angulus continetur, aequale segmento BH, quod subiiciatur esse maius circumferentia AB, minus autem complemento eiusdem circumferentiae AB. Igitur punctus H necessario cadet inter B, C signa. Et a puncto H ipsi DGF dimetienti parallela agatur HI. Atque segmenti IFE sinus rectus sit IK; et ipsius parallela sit acta LM aequalis sinui recto complementi tertii lateris, quod in proposito triangulo sphaerico subtenditur ei angulo, quem datum oportet efficere. Deinde CGE diametro parallelus agatur HNO, secans LM super N et IK super signo.

Et quia per constructionein duae rectae lineae IK et LM sunt parallelae, igitur per XXTX propositionem libri primi elementarum anguli ad N, O signa sunt aequales, videlicet angulus HNL aequalis angulo NOI; uterque enim rectus. Et quoniam duobus triangulis IHO, LHN communis angulus est NHL, igitur duo trianguli IHO, LHN sunt aequianguli et similes. Ergo per propositionem quartam libri sexti élementamm ratio ipsius ILH ad HL datur; est enim sicut IO ad LN ratio data. Et quia IH magnitudine datur - est enim dimetiens paralleli super B polo et secundum BH datam sectionem descripti -, igitur et HL, item et reliqua IL magnitudine datur. Est autem IL per ea, quae prius [IV, 1] ostensa sunt, sinus versus circumferentiae in parallelo IH similis angulo proposito, quem datum oportebat efficere.

Datis igitur tribus lateribus propositi trianguli sphaerici, etc.; quod oportuit demonstrare.

Propositio tertia.

Si autem in dato triangulo sphaerico trium datorum segmentorum duo segmenta propositum [angulum] continentia fuerint aequalia, idem propositus angulus datus angulus erit.

Haec propositio per praemissam et subsequentes quoque ostendi poterit. Nam si uniuscuiusque aequalium segmentorum complementum maius fuerit octava parte circui magni, id est maius gradibus XLV, ipsa propositio fiet per praecedentem propositionem; sin autem aecquale, per sequentem propositionem; aut [si] minus octava parte maximi circuli, sive grad[ibus] XLY, problema fiet per quintam propositionem.

Propositio quarta.

At si alterum duorum segmentorum, quae propositum ad B angulum comprehendunt, aequale fuerit complemento circumferentiae AB, id est segmento BC.

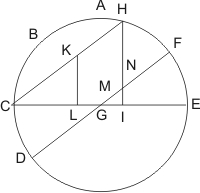Skizze Igitur ex C puncto ipsi DGF parallelus agatur CH, secans circulum ABCDE ad H signum. Et super CGE dimetientem perpendicularis agatur HI. Et complementi circumferentiae subtendentis ad B angulum propositum sit KL sinus.

Et quia, velut prius ostenditur, triangulus CKL similis triangulo CHI, ergo per propositionem quartam libri sexti eiementorum ratio HI ad KL erit sicut ratio ipsius HC ad CK. Et ex dimetiente FD auferatur DM secundum rationem HI ad KL. Igitur HI ad KL est sicut FD ad DM, Et dimidia ipsius HI sit HN. Et quia per constructionem FG dimidium est ipsius DGF dimetientis, ergo HN ad HI est sicut FG ad FGD. Igitur ex aequali HN ad KL est sicut FG ad DM. In hac autem proportione tres priores termini dati sunt. Nam HN dimidium est ipsius HI, quae rectus est sinus circumferentiae EFH per constructionem quoque datae; nam ipsa componitur ex duplo circumferentiae EF, id est ex duplo ipsius circumferentiae AB, Et KL aequalis est sinui recto complementi circumferentiae per hypothesim datae et subtendentis angulum ad B propositum. Et FG sinus totus. Ergo et quartus terminus DM datus est. Et quoniam per constructionem ratio FD ad DM est sicut ratio ipsius HO [ad] CK - est autem GK sinus versus circumferentiae in parallelo HC similis segmento magni circuli, [quo maximo semicirculo sublato] relinquitur circumferentia aequalis angulo ad B proposito [IV, 1] - , igitur FM sinus versus est propositi anguli ad B.

Ergo angulus ad B propositus est datus; quod oportuit demonstrare.

Propositio quinta.

Si vero alterum duorum segmentorum, quae propositum ad B continent angulum, maius fuerit complemento circumferentiae AB.

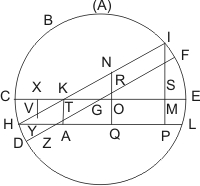Skizze Quod quidem complementum existit BC circumferentia, sitque illud aequale BCH segmento; itaque H punctus cadet inter C, D signa. Et ab H signo ipsi DGF dimetienti parallelus HKI agatur, secans dimetientem CGE super K signo. Rursus ipsi CGE dimetienti parallelus agatur HL. Et circumferentiae EFI sinus rectus sit IM.

His itaque dispositis, si circumferentia propositum ad B angulum subtendens quadrante minor extiterit, ergo parallela ipsius IM sinus recti aequalis recto sinui complementi circumferentiae ad B propositum angulum subtendentis cadet inter K signum et IM rectum sinum segmenti EFI. Sitque talis parallela NO; et productis IM et NO in partes M, O, donec occurrant ipsi HL, IM quidem in P, NO autem super Q.

Igitur, ut prius, erit ratio ipsius INH ad HN sicut IMP ad NOQ. Et sicut est IH ad HN, sic fiat FD ad DR, Et dimidia ipsius IMP sit IS. Igitur, ut prius ostensum fuit, ex aequali erit ratio ipsius IS ad NOQ sicut ratio ipsius FG ad DR. In hac autem proportione priores tres termini dati sunt; ergo et quartus terminus DB datus erit. Nam IS dimidium est ipsius IMP datae, quae componitur ex recto sinu IM segmenti EFI dati per constructionem et MP aequali recto sinui segmenti CH similiter dati. Pari ratione NOQ recta probatur esse data. Et FG datur; est enim totus sinus ex hypothesi. Igitur BR recta datur, quae est sinus versus seu sagitta propositi ad B anguH [IV, 1].

Propositus ergo ad B angulus datur; quod oportuit demonstrare.

Circumferentia deinde, quae propositum ad B angulum subtendit, aequante quadrantem, igitur HK erit sinus versus circumferentiae in parallelo HI, qua sublata ex semicirculo relinquitur circumferentia in eodem parallelo ad B angulo [subtensa]. Et super HL perpendicularis KA agatur; ergo iterum ratio ipsius IMP ad KA erit sicut IH ad HK. Et sicut IH ad HK sic fiat FB ad BT. Igitur, ut prius, ex aequaU IS ad KA erit sicut FG ad DT. Est autem KA data; aequalis enim existit recto sinui segmenti CH per constructionem. In eadem ergo proportione datis tribus prioribus terminis et quartus terminus BT datur, sinus scilicet versus circumferentiae circuli magni, qua sublata ex semicirculo relinquitur circumferentia aequalis ad B angulo proposito.

Igitur propositus idem ad B angulus erit iterum datus.

At circumferentia, quae propositum ad B angulum subtendit, quadrantem superante, igitur per superius ostensa sinus versus subtendentis in parallelo HI circumferentiae, qua dempta semicirculo eiusdem paralleli relinquitur circuinferentia similis proposito ad B angulo, erit miaor quam HK recta. Sit itaque talis sinus versus HV; et per V ipsi IMP parallelus agatur XVY, secans dimetientem CGE super Z, et HL super Y. Et quia ratio ipsius IMP ad VY est sicut IH ad HV, sit igitur FD ad DZ sicut IH ad HV; ergo ex aequali IS ad VY erit sicut FG ad DZ. At huius proportionis tres termini priores dati sunt; ergo et quartus terminus videlicet DZ datus erit. Nam YV reliqua est, si VX detrahatur sinui recto segmenti GH. Est autem XV aequalis sinui recto circumferentiae remanentis, si circumferentiae ad B angulo subtensae quadrans auferatur; ergo et VX datur; quare etiam VY dabitur. Et quoniam ratio ipsius IH ad HV est sicut FD ad DZ, ergo DZ datur, et erit sinus versus circumferentiae magni circuli, qua dempta ex semicirculo eiusdem circuli magni relinquitur circumferentia aequalis proposito ad B angulo.

Igitur idem propositus ad B angulus iterum datus erit; quod oportuit, ostendere.
Valid HTML 4.01 © Rainer Stumpe URL: http://www.rainerstumpe.de