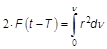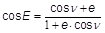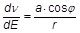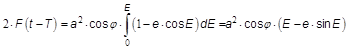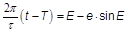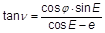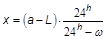Die Zeitgleichung

Beim Beispiel "Berechnung der Tageslänge" wurde eine Korrektur erwähnt, die als Zeitgleichung be­zeich­net wird. Die üblichen Quellen sind recht vage, was die Grundlage für diese Korrektur angeht. Fündig wurde ich in alten Lehrbüchern der Astronomie. Die Notwendigkeit, eine Zeitkorrektur bei der Be­stimmung eines Sternenortes anzubringen, kommt wohl deutliche nach Kepler auf. Zu dessen Zeit gab es noch keine Chronometer (die wurden erst zwischen 1778 und 1780 in England zur Längenbestimmung aus Sternenhöhen für die Navigation entwickelt). In diesem Zusammenhang wurde wohl deutlich, dass die Definition der Zeit eine grundlegende Bedeutung zukam. Denn es zeigte sich, dass die Zeit zwischen zwei Kulminationen der Sonne (Sonnentag) und die zwischen zwei Kulminationen eines Fixsterns (Sterntag) unterschiedlich sind — und sich dieser Unterschied auch noch im Jahresverlaufe ändert.

Als die im Quellenverzeichnis angegebenen Lehrbücher geschrieben wurden, hatten Isaac Newton bereits die Infinitesimalrechnung erfunden, und Carl Friedrich Gauss einen Formelapparat zur Bahn­bestim­mung von Himmelkörpern publiziert. Beides erleichterte die Berechnung, war aber nicht mehr so anschaulich wie Keplers Argumentation auf der Basis der Euklidschen Geometrie.

Zur Beobachtung der Fixsterne wird ein Koordinatensystem verwendet, das dem Äquatorsystem ähnelt, nur die Bezeichnungen sind andere. Entlang der Äquatorebene wird vom Frühlingspunkt aus die Rekt­aszen­sion α gemessen, der Winkel auf dem Meridian durch den Himmelspol ist ebenfalls die Deklination δ. Die Rekaszension wird in Stunden gemessen (Stundenwinkel). Steht die Sonne im Frühlingspunkt (um den 21. März), so geht sie etwa um 0 h Sternzeit durch den Meridian. Im Verlaufe des Jahres bewegt sich die Sonne auf der Ekliptik, und zur Herbst Tag- und Nachtgleiche geht sie um 12 h Sternzeit durch den Meridian. Bei einem jährlichen Umlauf kulminiert sie so zu allen Stunden des Sterntags mit 24 Stunden. Im alltäglichen Leben bezieht man die Zeit auf zwei aufeinanderfolgende Kulminationen der Sonne auf dem Ortsmeridian (wahrer Sonnentag) und der Stundenwinkel des Azimuth a ist die wahre Sonnenzeit.

Man stellt nun fest, dass sich die Rekaszension nicht gleichmäßig ändert. Der Grund liegt in der Form der Umlaufbahn: es ist eine Ellipse, und die Umlaufgeschwindigkeit folgt dem 2. Keplerschen Gesetz: die Fläche des im Zeitinterval vom Radiusvektor überstrichenen Ellipsensegments ist konstant (d. h. die Zeit zum Überstrichen ändert sich).

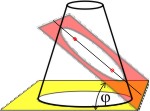Die Fläche der Ellipse ist A = π · a · b (a und b sind die große bzw. die kleine Halbachse). Mit der Definition der linearen Exzentriziät e² = a² - b² erhält man A = π · a² · √(1 - e²). Wenn die Erde die Umlaufzeit τ hat, so ist ihre Flächengeschwindigkeit F = A ⁄ τ = (π · a² · √(1 - e²)) ⁄ τ. Nun brau­chen wir einen Ausdruck für die lineare Exzentrizität und finden den bei den Kegelschnitten: e = sin φ. Setzt man die große Halbachse noch a = 1, so wird die Flächengeschwindigkeit F = (π · cos φ) ⁄ τ.

(Dieser Trick stammt von C. F. Gauss, der ja eine allgemeine, für alle Kegel­schnitte geltende Formel aus den Keplerschen Gesetzen und Newtons Gravitationsgesetzen abgeleitet hat: der Winkel φ im Verhältnis zum Öffnungswinkel bestimmt die Art des Kegelschnitts (Kreis, Ellipse, Hyperbel, Parabel).)

Bezieht man nun auf den Periheldurchgang der Erde zur Zeit T, so ist die Ellipsensektorfläche zum Zeitpunkt t F eine Funktion der Zeitdifferenz t - T. Die ist aber auch das bestimmte Integral
F(t - T) = ½ · ∫r² dν in den Grenzen von 0 und ν, wobei r der Fahrstrahl und ν sein Winkel mit der großen Achse zur Zeit t: die wahre Anomalie.

Bei der Ellipse gilt:

• .

• 
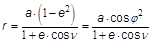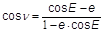
• und
• 

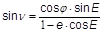
Durch Differenzieren der Formeln für den Fahrstrahl r erhält man:

Man kann aber näherungsweise die Differenz zwischen wahrer und mittlerer Anomalie als Reihe entwickeln. Man differenziert die Gleichung

• 
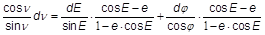
• oder
• 

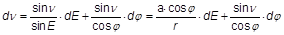
• aus dE = sin ν dφ
• 
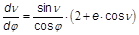
• und
• 

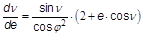
• P₀′ = cos M · ν₀′ = sin 2 · M
• Q₀′ = cos M
• ν₀″ = sin M · Q₀′ + 2 · 2 · P₀′ = ½ · sin 2 · M
• P₀″ = cos M · ν₀″ - sin M · ν₀′² + 2 · sin M = 9 ⁄4 ·sin 3 ·M + 1 ⁄ 4 · sin M
• Q₀″ = -2 · sin M · ν₀′ = -4 · sin M²
• ν₀″′ = sin M · Q₀″ + 2 · Q₀′ · P₀′ + 2 · P₀″ = 13 ⁄ 9 ·sin 3 · M - 3 ⁄2 · sin M

Die scheinbare Winkelbewegung der Sonne ist gleich der Winkelbewegung der Erde und man erhält die wahre Länge λ der Sonne, wenn man zu ν den Wert der Länge der Sonne beim Periheldurchgang der Erde ξ addiert. Die mittlere Länge Λ der Sonne ist M + ξ. Damit berechnet man die wahre Länge der Sonne (in Bogensekunden) mit der Gleichung:
λ = Λ + 6918,37″ ·sin M; + 72,52″ · sin 2 · M + 1,05″ · sin 3 · M
Da M = Λ - ξ ist, erhält man schießlich mit ξ = 280° 21′ 41,0″:

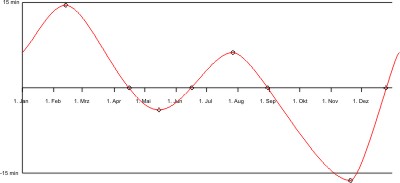
Die mittlere Länge Λ der Sonne berechnet man mit der obigen Formel in Sternzeit. Der Stundenwinkel zum mittleren Mittag der Sonne ergibt sich aus Λ - a daher auch in Sternzeit. Um den wahren Mittag zu erhalten subtrahiert man einen Wert von der mittleren Zeit: die Zeitgleichung x:

Die Funktion x der Zeitgleichung kann man nun differenzieren und eine Kurveninterpretation (wer erinnert sich noch an den Matheunterricht?) machen. Als erstes sucht man die Null-Stellen (a - Λ) = 0:
0 = 86,5″ · sin Λ - 596,6″ · sin 2·Λ + 431,1″ · cos Λ
daraus erhält man Λ₁ = 23° 16′ (15. April), Λ₂ = 83° 26′ (14. Juni), Λ₃ = 116° 15′ (31. August), Λ₄ = 273° 3′ (24. Dezember). Und man findet vier Extrema der Differenzialkurve:

+14 min 31 sec	-3 min 53 sec	+6 min 12 sec	-16 min 18 sec
12. Feb.	14. Mai	26. Jul.	18. Nov.

Da die Berechnung — wie man sehen kann — recht aufwändig ist, trägt man die Nullstellen und Extrema in ein Diagramm ein, und verbindet die Punkte mit einer schlichten Kurve. Die kann man dann durch Addition zweier Funktionen parametrisieren, und so zu einer "Formel" für Berechnungen kommen (siehe z. B. Wikipedia).

Quellen

1. Franz Brünnow: Lehrbuch der sphärischen Astronomie, 3. Auflage, Dümmlers Verlagsbuchhandlung, Berlin, 1871.
2. J. J. Littrow: Vorlesungen über Astronomie, Verlag von J. G. Heubner, Wien, 1830.
3. Carl Friedrich Gauss: Theoria Motus Corporum Coelestium in Sectionibus Conicis Solem Ambientum, Frid. Perthes und I. H. Besser, Hamburg 1809.
4. Carl Friedrich Gauss: Theorie der Bewegung der Himmelskörper welche in Kegelschnitten die Sonne umlaufen. Deutsch von Carl Haase, Carl Meyer Hamburg, 1895.