Erläuterung zum Poldreieck

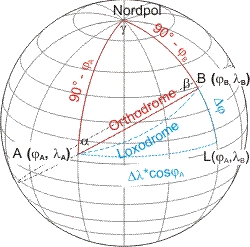Die Anwendung des sphä­rischen Poldreiecks ist etwas verwirrend: im Zusammenhang mit der Orthodrome wird der Seitencosinus-Satz in einer besonderen Form angewendet. Im Bild erkennt man aber auch ein recht­wink­liges sphä­risches Dreieck. Und das ist ja das Dreieck ALB mit den Katheten AL = γ = (λ_A - λ_B) · cos φ_A und LB = (φ_A - φ_B), und der Hypotenuse AB. Deren Länge ist auch die orthodrome Entfernung auf dem Großkreis von A nach B. (Weil alle Meridiane die Breitenkreise im rechten Winkel schnei­den.)

Nennen wir den Punkt des Nordpols im Poldreieck C. Man erkennt drei Dreiecke: ABC, ALC und ALB. Das Dreieck ABC ist nicht rechtwinklig, aber die Dreiecke ALC und ALB sind es jeweils. (ALC hat sogar zwei rechte Winkel: bei A und bei L.) Die gesuchte Drei­ecks­seite AB = c ist in zwei der Dreiecke enthalten: als Hypotenuse in ALB und als eine Seite im schief­wink­ligen sphärischen Dreieck ABC. Es gibt also prinzipiell zwei Möglichkeiten der Berechnung.

1. Im rechtwinkligen Dreieck ALB sind bekannt die Seitenlängen AL = a = cos φ_A ·(λ_A - λ_B) und LB = b = φ_B - φ_A. Zur Berechnung der Länge AB = c kann man nun den sphärischen Pytagoras anwenden: cos c = cot b · cot a.
   Damit ist diese Formel zur Berechnung ungeeignet! Der Cosinus muss zwischen -1 und 1 liegen, d. h. das Produkt aus den Cotangenten muss kleiner ±1 sein; da aber der Tangens und der Cotangens nur in engen Winkelbereichen kleiner ±1 sind, kann man die Formel nicht allgemein anwenden!
2. Im Dreieck ABC — einem schiefwinkligen — sind die beiden Seiten AC = a und BC = b bekannt, sowie der Winkel ∠ACB = γ. (Da die Breite eines Ortes vom Äquator (= 0°) zum Nordpol (= 90°) gezählt wird, sind a und b die Komplemete der Breiten von A bzw. B.) Man wendet daher den Seitencosinus-Satz an: cos c = cos a · cos b + sin a · sin b · cos γ.

Da die Seiten des Poldreiecks, die den Winkel γ am Pol einschließen, die Längen a = 90° - φ_B bzw. b = 90° - φ_A haben, und weil nach der Phasenregel cos α = sin (90° - α) und sin α = cos (90° - α) ist, wird der Seitencosinus-Satz umgeformt zu:

• cos c = sin a · sin b + cos a · cos b · cos γ =  sin φ_B · sin φ_A + cos φ_B · cos φ_A · cos (λ_A - λ_B).