Euclid, Buch VI, Lehrsatz 3
Die Abschnitte auf einer Dreiecksseite, die durch die Winkelhalbierende des der Seite gegenüberliegenden Winkels gebildet werden, verhalten sich wie die dem halbierten Winkel anliegenden Dreiecksseiten.
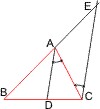 In einem Dreieck ABC halbiert man den Winkel bei A; die Winkelhalbierende schneidet die gegenüberliegende Seite BC im Punkt D. Zu der Winkelhalbierenden zeichnet man eine Parallele durch C und verlängert die Seite AB bis zum Schnittpunkt E. Da die Strecke AC die beiden Parallelen AD und CE schneidet, sind die Winkel CAD und ACE gleich, und die Winkel BAD und AEC ebenfalls (Winkel an Parallelen).
In einem Dreieck ABC halbiert man den Winkel bei A; die Winkelhalbierende schneidet die gegenüberliegende Seite BC im Punkt D. Zu der Winkelhalbierenden zeichnet man eine Parallele durch C und verlängert die Seite AB bis zum Schnittpunkt E. Da die Strecke AC die beiden Parallelen AD und CE schneidet, sind die Winkel CAD und ACE gleich, und die Winkel BAD und AEC ebenfalls (Winkel an Parallelen).
Und da AD die Winkelhalbierende ist, sind auch die Winkel BAD und CAD gleich. Somit sind auch die Winkel ACE und ACE gleich, was bedeutet, das Dreieck ist gleichschenklig und damit AC = AE. Und weil AD parallel zu EC (die einen Seite im Dreieck BCE) ist, ist das Verhältnis der Seiten DB : DC gleich dem Verhältnis AB : AE. Da aber das Dreieck ACE gleichschenklig ist, ist AC = AE (s.o.), somit ist DB : DC = AB : AC.