Die Keildreiecke

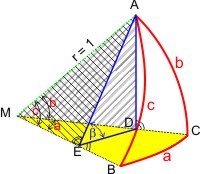Im ebenen Dreieck ADE ist A gleichzeitig eine Ecke des sphä­ri­schen Dreiecks ABC. Daraus folgt AM ist die Hypotenuse der rechtwinkligen Keildreicke ADM und AEM; ihre Länge ist der Ein­heits­radius r = 1 = AM der Kugel. Ein drittes Keildreieck ist DEM, mit DE = sin a und dem rechten Winkel bei E: ∠DEM = 90°, weil DE parallel zur Tangente an die Kugel in B ist, und der Ku­gel­ra­dius per definitionem senkrecht auf der Tangente steht.

1. Das Keildreieck AEM
   Bekannt sind:
   1. der Winkel ∠AME = c
   2. der Winkel ∠AEM = 90°
   3. die Hypotenuse AM = 1
   Damit ist das Dreieck hinreichend bestimmt, und man erhält mit den Definitionen der Winkelfunktionen:
   1. AE = sin c
   2. ME = cos c
   3. ∠EAM = 90° - c
2. Das Keildreieck ADM
   Bekannt sind:
   1. der Winkel ∠AME = b
   2. der Winkel ∠ADM = 90°
   3. die Hypotenuse AM = 1
   Damit ist das Dreieck hinreichend bestimmt, und man erhält mit den Definitionen der Winkelfunktionen:
   1. AD = sin b
   2. MD = cos b
   3. ∠DAM = 90° - b
3. Das Keildreieck DEM
   Bekannt sind:
   1. der Winkel ∠DEM = 90°
   2. der Winkel ∠DME = a
   3. die Hypotenuse MD = cos b
   4. die Kathete EM = cos c
   Damit ist das Dreieck hinreichend bestimmt, und man erhält mit den Definitionen der Winkelfunktionen:
   1. ED = MD · sin a = cos b · sin a
   2. ME = MD · cos a = cos b · cos a
   3. ∠MDE = 90° - a

• 1.b.: ME = cos c
• 3.b.: ME = cos b · cos a

• cos c = cos b · cos a