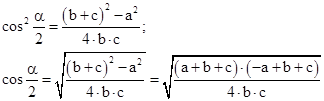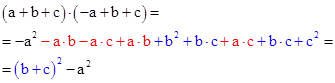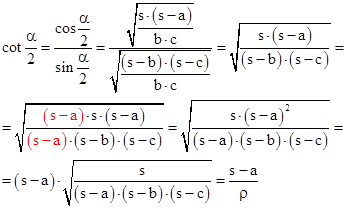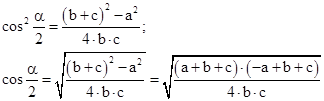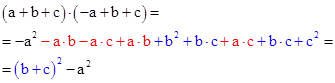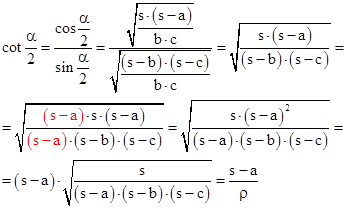Zum Cotangenssatz
|
| In den Gleichungen des Cosinussatzes mit dem halben Winkel: |
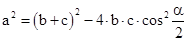 |
| und |
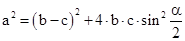 |
| bringt man die Quadrate der Seiten auf die linke Seite: |
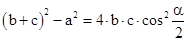 |
| und dividiert durch den Faktor vor dem Cosinus und zieht die Wurzel: |
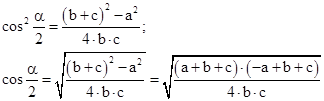 |
| Prüfung der Umformung des Zählers der Wurzelbrüche: |
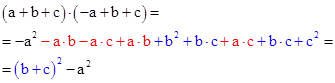 |
| Nun setzt man: |
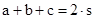 |
| ergänzt den linken Klammerausdruck um -a +a (blau) und faßt zusammen: |
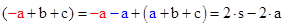 |
| Man erhält also für den Cosinus des halben Winkels: |
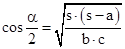 |
| und nach dem analogen Formalismus für den Sinus: |
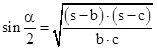 |
| Schließlich dividiert man den Cosinus durch den Sinus, kürzt den Bruch, ergänzt um die rote Differenz und setzt den Ausdruck für den Radius des Inkreises ein: |
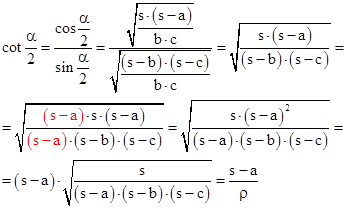 |
|
 |
|
|