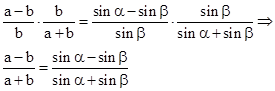
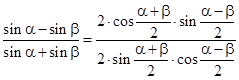
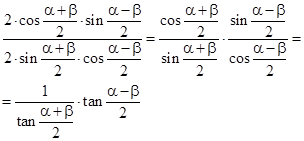
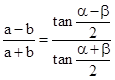
Der Tangenssatz
Eine beliebige Gleichung des Sinussatzes:
wird auf beiden Seiten um ±1 erweitert:
und umgeformt:
nun dividiert man die Gleichung mit "-" durch die mit "+" (bzw. multipliziert mit dem Kehrwert) und kürzt: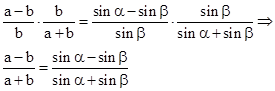
nach dem Additionstheorem erhält man: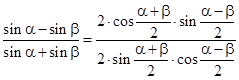
und weil:
ist mit:
 
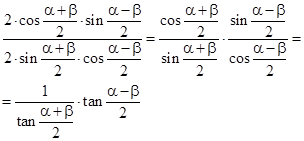aus dem Sinussatz ergibt sich also: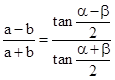