Das hölzerne Rad mit Achse im Stadtmuseum Ljubljana

Im Jahr 2002 wurde in einem Moor östlich von Ljubljana ein hölzernes Rad mit der zugehörigen Achse gefunden. Es ist über 5.100 Jahre alt. In der Nähe wurde eine Pfahlbausiedlung gefunden. Solche Pfahlbausiedlungen sind im ganzen Alpenraum bekannt, auch Fragmente von Holzrädern (z. B. im im Federseemuseum). Das Rad im Stadtmuseum Ljubljana ist fast vollständig erhalten zusammen mit der zugehörigen Achse. Man kann also die Konstruktion analysieren.

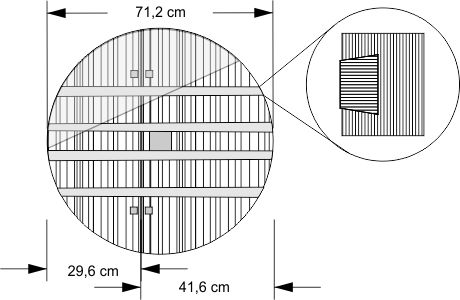
Schema — Abb. 1
Nach der Zeichnung von T. Korošec in Quelle [1]

Das Rad mit einem Durchmesser von 71,2 cm und einer größten Dicke von 6 cm besteht aus 2 verbundenen Planken aus Eschenholz (Brinell-Härte längs: 65, quer: 37-41 N ⁄ mm²) mit 4 Riegeln aus Eichenholz (Brinell-Härte längs: 64, quer: 41 N ⁄ mm²). Der linke obere, grau unterlegte Teil des Rades fehlt. Es gibt eine zentrale quadratische Öffnung zur Befestigung an der Achse, und vier paarweise angeodnete Löcher (graue Füllung) dicht an der Trennlinie der Radteile. Die Öffnung ist etwas vom geometrischen Mittelpunkt des Rads entfernt, was vermuten läßt, dass die Hersteller den Zirkel nicht kannten — wie die Erbauer der Kreisgrabenanlagen. Vermutlich waren Holzpflöcke in die Löcher gesteckt und jeweils auf der Vorder- und der Rückseite zusammengebunden. Die Riegel haben einen trapezförmigen Querschnitt und sind in Nuten der Radplanken eingepaßt. Im Querschnitt ist das Rad konvex, in der Mitte ist es 6 cm dick.

Die wirkenden Kräfte bei der Drehung des Rades

In dem Augenblick der Drehung um α = 10°, zu dem die kleinere linke Radplanke den Boden berührt, lastet das Gewicht der Achslast G auf dem kleineren Radteil, das führt zur Scherkraft S, die von der Haftreibung an der Grenzfläche und den Stabilisierungsriegeln kompensiert werden müssen. Zur Berechnung wird die Gewichtskraft G in eine Komponente parallel S zur Trennlinie und eine senkrecht dazu D nach den Regeln der Vektorgeometrie zerlegt. Dabei ist ein rechter Winkel zwischen D und S (90°) und der Winkel zwischen S und G ist gleich dem Drehwinkel des Rades α.

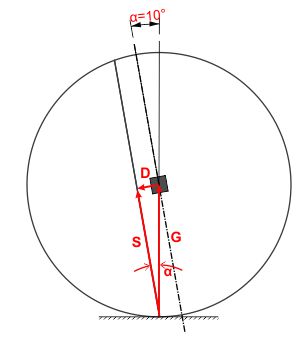
Kräfteverteilung01 — Abb. 3: Drehung um 10°

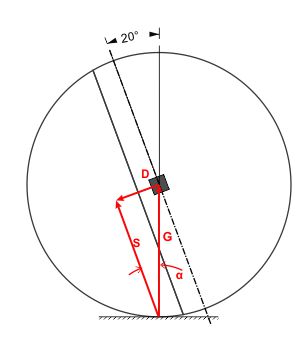
Kräfteverteilung02 — Abb. 3: Drehung um 10°

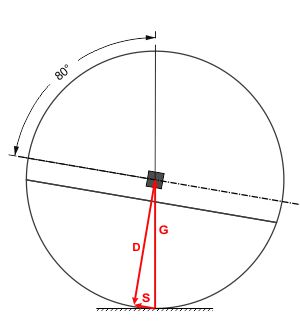
Nach der Definition der Winkelfunktionen erhält man aus dem Winkel α die Schwerkraft S = G · cos α und für die zusätzliche Andruckkraft D = G · sin α. Dreht sich das Rad weiter (Abb. 4), verändern sich S und G.

Die mechanischen Eigenschaften des Holzes

Die Kraft Scherkraft, die der Verschiebung der beiden Holzteile entgegen wikt, ist die Haftreibungskraft F_H. Sie hängt nur von der Anpresskraft D und einer Materialeigenschaft, dem Haftreibungskoeffizienten μ_H, nicht von der Fläche, ab:

-S = F_H = μ_H · D

Für den dimensionslosen Haftreibungskoeffizienten bei Holz auf Holz gilt:

μ_H = 0,5

Bei einer Raddrehung um 10° (Abb. 3) und einer Last von 100 kg beträgt die Scherkraft S = 100 kg · cos α = 98,5 kg. Die Druckkraft D = 100 kg · sin α = 17,3 kg. Der Scherkraft S entgegen wirkt die Haftreibung F_H = 0,5 · 17,3 kg. Die Differenz S - F_H = 81,2 kg muss also von den angebrachten Fixierungen kompensiert werden.

Die Fixierung mit den Pflöcken durch die kleinen Löcher in Abb. i hängt von der Elastizität des Bindematerials ab. In Frage kommen Lederstreifen, Tiersehnen und Pflanzenfasern. Alle diese Materialien sind elastisch und können die auftretenden Kräfte nicht vollständig aufnehmen. Vermutlich wurden sie nur vorübergehend angebracht um die trapezförmigen Nuten für die vier Riegel zu fräsen.

Die Riegel sind aus Eichenholz und so angeordnet, dass ihre Faserrichtung senkrecht zu der der Radteile verläuft. Sie sind an der Schnittstelle der Radteile etwa 20 mm dick und 20 mm breit. Die Druckfestigkeit von Laubholz beträgt senkrecht zur Faser f = 8,0 N ⁄ mm² [2]. Jeder der Riegel kann also etwa 325 kg aufnehmen ohne Festigkeit zu verlieren, vorausdesetzt, der Spalt ist nahe Null, und die Passung in die Nut ist über die gesammte Fläche ohne Lücke. Das Rad ist also mit ausreichender Sicherheit konstruiert, um die durch das Arbeiten des Holzes bei der belasteten Rotation zu berücksichtigen.

Anton Velušček, Katarina Čufar, Martin Zupančič: Prehistoric wooden wheel with an axle from the pile-dwelling Stare Gmaijne at the Ljublansko Barje. in: Anton Velušček (Herausg.): Stare Gmajne pile-dwelling settlement and its era. 2009.
Anton Schweizer: Formelsammlung und Berechnungsprogramme