Io: Keppleri
Harmonices Mundi Liber II.
De Congruentia Figurarum Harmonicarum.
Prooemium.
Essentiam singularum Figurarum Regularium Mentalem seu νοερὴύ hactenus explicavi: sequitur earum junctarum Proprietas, & veluti Effectus intra Geometriam, qui est Congruentia vel Insociabilitas. Non sunt enim ejusdem latitudini, Demonstrabilitas & Congruentia, cum illa singularum fit, & cum ipsa duplicatione continua laterum unius figurae in infinitum excurrat; ista certis coartata Iegibus, quibus plures figurae in unam societatem, vocantur, ob angulorum incrementa seipsam praepediens, cito desinat. Et quamvis delectus sit graduum scientiae demonstrationisque, & plurimum difFerant nobilitate, illae quas nos explicavimus, ab ijs quas dimisimus sine nomine: non tamen ne cum hac quidem demonstrationis nobilitate, Congruentia plane pari passu ambulat adeoque unum alterius causa non est, sed utrumque ex eadem communi causa (quae est angulorum figurae aptitudo) , quodque tamen suis legibus, dependet. Quantopere vero necessaria sit nobis haec quoque speculationis pars, ex ipso totius operis instituto videre est. Cum enim originem Harmonices , eiusque Effectus in toto Mundo praestantissimos, explicandos sumpserimus; quomodo de congruentia figurarum, quae sunt proportionum Harmonicarum scaturigines, verba nulla faciamus? Cum idem sonet Lacinis Congruere & Congruentia; quod Graecis ἁρμὁττειν & ἁρμονια? cum hic figurarum effectus intra Geometriam intraque Architectonices partem illam, quae circa Archetypos versatur, sit quaedam velut imago & praeludium Effectuum extra Geometriam, extraque mentis conceptus, in ipsis rebus naturalibus & coelestibus? cum proprietas haec congruentiae, quae in structuram & corporationem aliquam exit, talis sit, ut vel ipsa Mentem speculatricem invitet ad aliquid etiam foris faciendum, creandum, corporandum: utque latens inde ab aeterno in superbenedicta mente divina, per Idearum ordines, tanquam bonum summum, sui communicativum, continerio in sua abstractione non potuerit quin in Creationis opus prorumperet, Deumque Creatorem efficeret corporum sub jisdem figuris conclusorum. De hac igitur figurarum Congruentia paucis agam, cum demonstrationes difficiles nequaquam sint, nec alio pene apparatu, quam ipsa figurarum pictura indigeant.
De Figurarum Regularium Congruentia.
I. Definitio.
Congruentia alia planitiei est, alia in solido. In Plano Congruentia est, cum anguli figurarum plurium singuli sic ad puncltum unum concurrunt, ut nullus relinquatur hiatus.
II. Definitio.
Haec perfecta dicitur, cum figurae cujusque concurrentis anguli omnes eadem specie concurrunt, ut ita omnes concursus inter se similes sint, & concursuum ordo in infinitum continuari possit.
III. Definitio.
Perfectissima, cum etiam figurae concurrentes in pIano sunt ejusdem speciei.
IV. Definitio.
Imperfecta, cum major quidem figura undique similibus concursibus sepitur, neque tamen datur continuatio in infinitum, aut datur, quidem, sed non sine admixtione diversarum concursus specierum. Imperfecta deterioris gradus, cum major figura non omnibus angulis simili specie concurrere apta est.
V. Definitio.
Solida congruentia est, & figura solida, cum anguli singuli pIurium planarum figurarum, angulum constituunt solidum, aptatisque figuris regularibus vel semiregularibus, nullus restas hiatus inter latera figurarum, obviantia sibi in opposita solidae figurae parte, qui non claudi possit figura speciei unius ex adhibitis, vel saltem Regularibus.
Nota, quod sit alia congruentia, non planarum figurarum ad figuram solidam formandum, sed ipsarum solidarum figurarum inter se, ad locum solidum circa unum punctum explendum: hujusmodi figurae corporae sunt tantum duae, Cubus & Rhombus Dodecahedricus. Nam octo anguli Cubi concurrunt ad unum punctum, & unum undiq locum explent. Rhomhus vero habet duo genera angulorum, trilineares obtusos octo, & quadrilineares acutos sex. Igitur obtusi quatuor, congruunt ad locum explendum, acuti vero sex: quale struunt aedificium Apes, cellis contiguis, ut unam circumstent a fundo tres adversis fundis, a lateribus sex; & possent etiam anterius tres aliae circumstare ad figuram absolvendam, nisi fores oportuisset esse patretes. De hac vero solidarum figurarum congruentia nos hic non agimus.
VI. Definitio.
Perfectissima solida Congruentia, solidaque figura est, cum etiam Plana congruentia sunt ejusdem figura omnia.
VII. Definitio.
Haec vel est regularis rota, cum Plana sunt regularia, habetque omnes angulos in eadem sphaerica superficie, & inter se similes.
VIII. Definitio.
Vel est semiregularis, cum Plana sunt semiregularia (vide libr. I. def. III.) habetque angulos solidos numero linearum distinctos & dissimiles; non tamen plurium, quam duorum generum; nec in pluribusq duabus sphaericis superficibus, uno centro descriptis, ordinatos: & singulorum generum angulos tot numero, quot habet una Regularium.
Non obstat, Congruentiam hanc solidam, perfectissimam dici: nam quae planis ejus inest imperfectio, solidationi non dedet adscribi, sed ei accidit. Dicitur tamen aequivoce perfectissima, haec semiregularis.
IX. Definitio.
Perfecta inferioris gradus est, cum Plana regularia, & anguli omnes in eadem superficie sphaerica, & inter se similes sunt: sed Plana tamen diversarum specierum, singularum quidem tot numero, quot sunt in una perfectissimarum figurarum, se non minus quam 4, quot ad minimum Planitiebus solida figura terminatur.
X. Definitio.
Imperfecta congruentia seu figura est, eum caeteris manentibus, major figura non saepius quam semel aut bis invenitur.
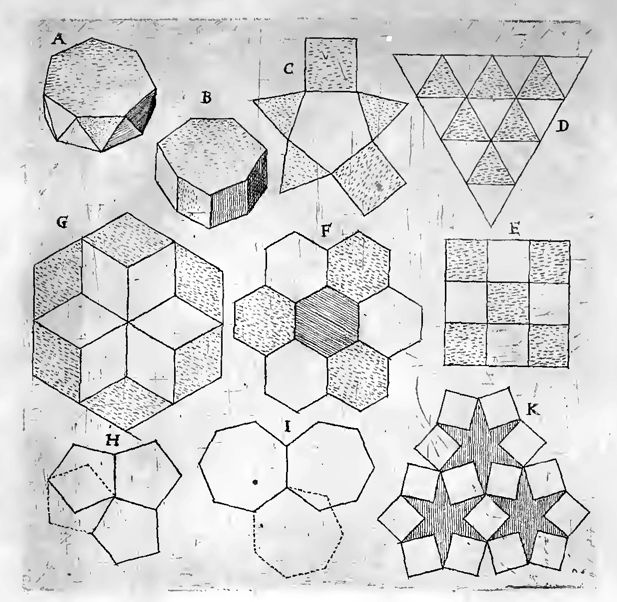
Fit enim figura illic parti quam toti, hic planae quam solide similior; eum omni solida ad minimum 4 superficiebus terminetur. Ut in typis ex aere sequentibus ad literas A, B, ubi major figura est Heptagonus. Classes istae duae cum ipsorum majoris figurae laterum numero excurrunt in infinitum; initio facto a Trigono utrinque quod in classe A, est ex perfectissimis regularibus congruent ii; transitu vero facto per tetragonum; & tunc inclasse B, incidimus iterum in unam perfectissimam regularem congruentiam; ceterae omnes imperfectae sunt.
XI. Definitio.
Semisolida est, quae non sustinet omnes definitionis quintae particulas; ut cum aptatis figuris planis, congruentia non plane in seipsam redit, sed relinquit hiatus; de caetero tueans praescripta Def. VI & VII.
XII. Definitio.
Figura Planae congruae sunt, quae vel solidam figuram concludunt, vel planitiem sine hiacu explent, existentes ipssae figurae Regulares vel semiregulares.
XIII. Definitio.
Incongruae dicantur illae figurae planae ReguIares circuIoque inscriptae (siquidem sunt inscriptiles) quae neque solidam figuram sphaerico inscriptilem secumipsae, aut cum alijs suae vel alterius classis, efformant, nisi imperfectam tantum; neque planum sternunt vel ipsae inter se singulae, vel cum Stellis suae classis, vel cum figuris & stellis classis alterius circumcirca.
Ubi nota excludi septangulum & talia, non obstante, quod bina parallela septangula vel septem quadratis, vel quatuordecim triangulis adjuta regularibus, solidum omnino claudunt,-quia tantum bina septangula concurrunt, fitque figura disciformis & planae similis, nequaquam vero globiformis, sphaeroides. Vide in figura ex aere fol. 53. seq. literas A. B. Sic etiam excluditur Quindecangulum, non obstante, quod aliquibus angulis cum figuris cognatis locum in plano explet; quia hoc non facit circumcirca omnibus angulis.
XIV. Propositio.
Angulorum planorum non pauciores quam terni in plano congruut.
Nam circa quodlibet concursus punctum est summa quatuor Rectorum angulorum: at nullius figurae angulus aequat summam duorum Rectorum, igitur duo quanticunque anguli, sunt adhuc minores quatuor rectis: duo igitur non explent planitiem, per Def. I.
XV. Propositio.
Angulorum planorum non pauciores,quam terni, ad solidum angulum formandum congruunt vel assurgunt.
Bini enim non lateribus tantum, sed totis planitiebus congrueret, nihilque de corpore solido complecterentur : quod est contra def. Anguli solidi ap. Euclidem.
XVI. Propositio.
Angulorum, in plano congruentium, summa semper est 4 rectorum, nunquam major: congruentium in solido est minor hac summa.
In plano n. non plures 4 rectis unum punctum circumstant: ergo cum aequatur summa 4 rectorum, tunc hiatus nullus relinquitur, & per def. I. congruentia tunc est in plano. Si planum sternut anguli, ad soliditatem non assurgut. Et vicissim; Si anguli aptati in plano relinqunt hiatum, quando sc. sunt minores 4 rectis, tunc adductis duobus lateribus circa hiatum, & excluso hiatus, necesse est, assurgere angulum & solidari. In figura H typiaenei Fol. seq. 53, sunt piclitrae Pentagoni in planitiem strati & hiantes.
XVII. Propositio.
Figura imparilatera, cujus aptantur lateribus, figurae duarum specierum, non potest aequali forma omnibus angulis concurrere vel in plane vel in solido.
Nam sit in uno ipsius angulorum, ut ejusdem speciei figurae utrinque stent, -quod in caeteris angulis non sit. Hujus rei causa vide figuram C, typi aenei seq.
XVIII. Propositio.
Planum locum perfectissime explent, Plana ejusdem figurae tantum Tria, Trigoni seni, Tetragoni quaterni, Hexagoni terni.
Nam per XXXIII primi hujus, Trigoni angulus est 2 tertiae unius recti, sex ergo anguli senum Trigonorum, sunt 12 tertiae, id est, 4 integri. Vide D.
Sic Tetragoni angulus est unus rectus , quatuor ergo quaternorum Tetragonorum anguli, faciunt quatuor rectos. Vide E. Sic Hexagoni-angulus est octo sextae unius recti; tres ergo trium figurarum, faciunt 24 sextas, id est, 4 rectos, vide F. At Pentagoni angulus est minor Hexagonico,- tres ergo sunt minores 4 rectes; tres ergo hiant. Idem est major Tetragonico: quatuor ergo Pentagonici sunt majores 4 rectis, ergo non capiuntur in uno hco plano, per XVI hujus. Hac de causa vide H, cum quarto Pentagono punctis signato. Sic Heptagoni, & omnium majorum figurarum, angulus major est Hexagonico; tres ergo Heptagonnici superant 4 rectos. Vide I, ubi duorum Heptagonorum partes in piano tegunt locum eundem.
Huc refer Rhomos, constantes ex binis Trigonis Regularibus singulos. Congruunt enim perfectissime, ut Regulares Hexagoni, etsi ipsi sint figurae semiregularis. Vide hanc congruentiam in schemate seq. Ex aere, Litera G.
Huc etiam refer stellas ex Dodecagono sexangulas, ex sectis senis radijs: apud literam K: venit enim in locum exsecti radij, cavus angulus, recto aequalis. Igitur tres Tetragonici & tres talium steliarum radij, implent locum. Nam Hexagonus dividitur in talem stellam & sex dimidios Tetragonos.
XIX. Propositio.
Ex planis duarum figurarum impletur locus planus sexies; bis ex quinque, semel ex quatuor, ter ex tribus angulis.
Sena enim plana coire non possunt, ut eorum unius angulus sit major Trigonico: quia primi Trigonici quantitas est duae tertia unius recti; itaque hoc sexies sumptum facit 12 tertias, seu 4 rectos, V no igr horum 6 majori existente, ut (c. sit figurae pIurilaterae, superantur 4 recti: & tunc planities non sternitur, per XVl hujus.
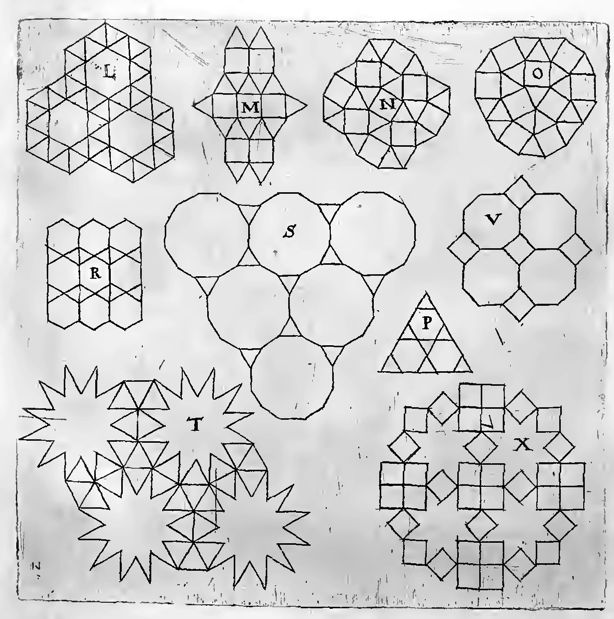
Quina vero plana tunc coeunt, si quatuor Trigonicis jungatur unus; aequans duos Trigonicos, talis vero est Hexagonicus; forma qualis literis L.
Vel si tribus trigonicis duo teiragonici jungantur; quia aequant tres alios trigonicos. Forma qualis in M, vel qualis in N, sc. continue uniformis; vel denique, qualis in O, difformis continuationis.
At si Trigonicos duos, Tetragonicos tres sumpseris, ij jam quatuor rectos superabunt: multo magis si majores duo accersantur anguli ad duos trigonicos.
Quaterna vero duorum specierum coeunt, si Trigonicis binis, jungantur bini Hexagonici. Forma qualis in P, vel qualis in R.
Aliter utcunque copulaveris quaterna: semper vel plus efficies, vel minus quam quatuor rectos; eoque locum planum non sternes.
Ternos igitur si jungamus, ea ventes, ne fiat plures quam duae species; primum non poterunt esse duo Trigonici, nec duo Tetragonici, non superarent enim duos rectos, & reliqueretur pro tertio, quod nullus unus & solus implet.
Uno vero inter ternos Trigonico posito, congruunt duo Dodecagonici: estque continuatio possibilis; nec admiscentur alij concursis, Forma hujus planiciei videatur littera S.
Huc refer stellam Dodecangulam, ex eo fundamento, quod ejus angulus cavus aequat Trigonicum: itaque dividuus est Dodecagonus in stellam & 12 Trigonos; Ergo quinque Trigonici & duo Radij duarum stellarum coeunt: forma continuabilis, spectetur litera T.
Et uno Tetragonico inter ternos assumpto, congruunt duo Octogonici, estque continuabilis & haec forma: videatur litera V.
Huc refer stellam Octogonicam, ex eo fundamento, quod ejus angulus cavus aequat Tetragonicum: itaque dividuus est Octogonus in stellam & octo triangula Tetragonica, quorum duo efficiunt Tetragonum.. Et sic Tetragonici tress & duarum stellarum radij duo, implent locum: forma mixta, ut litera X: vel aliter etiam mixta, ut litera T.
Dimissis jam in ternis coaptandis, Trigomco & Tetragonico, si ad Pentagonicum veniamus, eorum possunt sumi duo, quia superant juncti 2 rectos: & congruit in locum reliquum Decagonicus unius: coronatur enim Decagonus Pentagonis decem: sed non continuatur pure haec forma. Vide Schema litera Z interius.
Huc ergo refer stellam Pentagonicam, cum sunt Pentagonici tres, & unius stelae radius; quia cavus stellae angulus capit etiam unum angulum pentagenicum, non minus, quam Pentagonicorum trium hiatus, capit radium stellae. Vide eadem litera Z exterius.
Quamquam ne sic quidem continuatio succedit in infinitum; est enim insociabile hujus sectae regnum, quae paucis suorum adscitis, statim se munit: Ecce formas has duas etiam aliter, litera Aa.
Quod si continuare omnino velis, monstra quaedam sunt adsciscenda, duo Decagoni inter se commissi, extritis in utroque binis Lateribus; sitque series structura quinquangula etiam in infinita continuatione, sic ut in prima & angustissima quinquangulari serie sint Decagoni quinque, nullum monstrum intermedium: In secunda laxiori, series lineares Decangulorum mediant singulae copulae ex binis Decagonis inter se commissis; In tertia singulorum angulorum loca occupant singulae copulae ex binis Decagonis inter se commissis, quas mediat Decagonus unus: In quarta stant rursum integiri Decagoni in angulis, mediantque binos angulos bini Decagoni, dispositi aequalibus intervallis: In quinta stant stellae cum singulis extremis radijs in singulis angulis, implent vero lineas bini Decagoni integri, & in medio, binae commissurae Decagonorum. Et sic consequenter, una quaelibet forma quinquangula fert novi aliquid. Structura est laboriosissima & artificiosissima, visenda id eandem literam Aa.
Huc etiam refer stellam Decangulam, in cujus cavum angulum congruit angulus Pentagoni & vicissim radij bini Trideciles, cum binis Pentagonicis congruunt & implent locum solidum. Haec forma recipit inaequales Pentagonos: & lices sit continuabilis, recipit tamen in medium vacuos Decagonos hiulcos. Forma est visenda litera Bb.
Pentagonis unus in ternorum planorum copulam assumi non potest, nam ej angulus habet sex quintas unius recti, per XXXlJI Lib. I: ergo angulis duobus reliquis relinquerentur 14 quintae, cuilibet 7 quintae; qualem nulla figura habet. Nec sumi possunt Hexagoni duo: nam residuum est etiam Hexagoni angulus & sit forma superius relata, cum nos hic quaeramus structuras ex duabus speciebus, non ex unicae speciei figuris. Per sequentes plurilateras figuras, quarum angulus major est Hexagonico, subtractis duobus angulis a 4 rectis, relinquitur pro reliquo minus, quam habet Hexagonicus: uno vero subtracto, minus relinquitur pro duobus reliquis, quam habent duo Hexagonici. Atqui de ijs figuris, quae pauciores & minores habent angulos, quam Hexagonus, jam antea transactum nobis est, quae & quot esse possint, quando terni sternunt planitiem.
XX. Propositio.
Ex planis angulis trium specierum, locus planus congrue impletur quater.
Hic non tolerantur tres pluresve trigonici; faciunt enim tres anguli Trigonici duos rectos; relinquitur minus, quam facit summa minimorum post illos, Tetragonici sc. & Pentagonici. Ob id neque duobus Trigonicis sociandi duo Tetraqonici, aut majores, quia non relinquerentur satis pro angulo figurae tertiae speciei.
Ergo si Trigonici sint duo, & Tetragonicus unus; sociabitur illis Dodecagonicus; non tamen continuatur Forma: vide literis Cc. Dd. Ee, tres formas, omnes ad primum earum pertinentes.
Huc etiam stella Dodecagonica referatur, ut supra. Nam quatuor Trigonici, unus Tetragonicus unus & unus stellae radius impiebunt locum. Ecce formas Ff. Gg. Hh.
Trigonicis duobus si Pentagonicus unus jungatur, residuum erit incongrum, 32 decimae quintae; nullus enim angulus habet 16 decimas quintas. Sin unus addatur Hexagonicus trigonicis duobus; residuus etiam Hexagonicus erit, & forma erit una ex superioribus. Non poterunt igitur porro esse bini Trigoni.
Ergo si sit Trigonicus unus, ei tres Tetragoni non addentur, nimum enim conflatur: nec spacij satis angulo tertiae speciei relinquitur.
Addantur uni Trigonico duo Tetragonici; in residuum ad quatuor rectos congrust Hexagonicus; forma duplex, Literis Ii continuabilis, Kk non continis abilis sine mixtura. Estque hic casus secundus.
Trigonicus unus cum Pentegenicis duobus non jungitur, restat enim hiatus 14 quindecimarum unius recti, alienus a Regularibus figuris: nec cum Pentagonico uno; rursum enim restant 32 quindecima, cum nulla regularis figura habeat 76 quindecimas: nec cum Hexagonico uno; faciunt enim 2. rectos, cum nullus solus angulus fiat tantus; dimidium vero hujus sit quantitas Tetragonici, de quo jam est actum: nec cum Heptagonico vel Octogonico, vel Enneagonico singulis; restarent enim pro angulo tertiae speciei figurarum, vel 40 Unes vicesimae, vel 21 sextae, vel 16 nonae, quales nulla Regtularis figura habet.
Ergo Trigonicus unus cum Decagonico uno compositus, reliquit hiatum, 26 quindecimas, quantus est Pentekaedecagonicus. Hic est quidem congruentias, sed inchoatae saltem. Nam Pentekaedecagoneus est impari latera; quare per XVII. miscentur diversae concursuum species, in ejusdem figurae angulis. Decagonus quidem pari numero laterum, praecingi posset alternis Trigono & Pentekadedecagono, sed statim duo tales Pentekaedecagoni in se mutuo incurrunt, seque impediunt.
Ulterius Trigonicus cum Hendecagonico non potest jungi, relinquuntur enim 56 Tresettricesimae, qualem angulum nulla figura Regularis habet.
Denique, Trigonicus cum Dodecagonico relinquit hiatum Dodecagonicum, de qua forma jam est dictum.
Si Trigonicus majoribus jungeretur, minor fieret hiatus, cum de minoribus jam sit actum. Et sic transactum est cum Trigonico; inter tres species admittendo.
Tetragonici anguli plures uno, ablati a 4 rectis, non relinquunt satis spacij pro duarum specierum duobus angulis, quippe qui juncti majores fierent duobus recta.
3. Tetragonicus unus, junctus uni Pentagonico, relinquit hiatum pro Icosigonico. Sociatur igitur Icosigonus omnibus angulis, congruitque legitime: at non continuatur hic ordo versus exteriora. Est ergo congruerentia imperfecta. En figuram litera Ll. Hic tertius est casus.
4. Tetragonicus Hexagonico junctus, hiatum relinquit pro Dodecagon. Ecce figuram litera Mm: Hic quartus & ultimus est casus.
Huc refer stellam Dodecagonicam, quam implent duodecim Trigoni: ut sic quatuor hic anguli concurrant ad implendam soliditatem, duo Trigonici, Tetragonicus, Hexagonicus, & radius stellae. Ecce figuram litera Nn.
Tetragonicus Heptagonico additus, relinquit hiatum 11 septimas, qualem angulum nulla habet figura Regularis. Additus Octogonico, relinquit hiatum Octogonicum: de qua forma supra. Transactum igitur est cum Tetragonico.
Pentagonicus cum Hexagonico, relinquit hiatum 22 quindecimas: cum Heptagonico, 48 tridesimas quintas: Cum Octogonico, 13 decimas, cum nullus regularis figura tantus sit angulus: & jam hiatus incipit esse minor angulo Octogonico, quiest 15 decimae. Atqui nos jam illas absolvimus, quae sunt mimnorum angulorum. Transactum igitur est cum Pentagonico.
Hexagonicus triplex implet locum planum, ergo non potest misceri cum duobus se majoribus. Et sic transactum est cum mistione trium figurarum.
XXI. Propositio.
Quatuor vel plurium specierum figurae planae, non congruunt angulis singulis ad implendum locum solidum.
Minimi enim anguli quatuor sunt hi, Trigonicus, Tetragonicus, Pentagonicus, Hexagonicus. At horum primus & ultimus aqeuant duos rectos, secundus est rectus, Tertius vero superat rectum una parte quinta unius recti. Sunt igitur juncti majores quatuor rectis: quare per XVI, non congruunt. Multb magis igitur superabuntur quatuor recti a majoribus angulis.
XXII. Axioma.
Cum duo plani non sunt majores tertio, non formant cum illo angulum solidum.
XXIII. Propositio.
Duo anguli plani, figurae imparilaterae, cum uno speciei alterius coeuntes, non formant regulare aliquod solidum.
Nam per XVIII, anguli solidi fiunt dissormes, contra def. a V in X.
XXIV. Propositio.
Tres anguli plani, trium distinctarum speciae figurarum, unius imparilaterae coeuntes, non absolvunt figuram solidam perfectam.
Rursum enim per XVII, solidi fiunt diversiformes, quod est contra definitiones.
XXV. Propositio.
Congruentiae Figurarum pIanarum ad solidam figuram formandam, perfecttissimae & regulares, sunt quinque.
Est scholion ad ultimam ultimi Euclidis. Nam per XV hujus, incipimus a ternis angulis, & per XVI, definimus insenis Trigonicis, in quaternis Tetragonicis, & in ternis Hexagonicis, quia per XVI hi aequant 4 rectos.
Tres igitur Trigoni, singulis angulis congruentes, minus quam 4, id est duos angulos planos rectos efficiunt; coaptatis igitur tribus trigonis, hiatus impletur quarto Trigono. Hinc Tetrahedron, vel Pyramis.
Quatuor Trigoni, singulis angulis congruentes, efficiunt 8 tertias, quod minus est quam 12 tertiae, seu 4 recti; fitque junctis trigonorum lateribus Pyramis, basi quadrilatera hiante; cui ex adverso alia talis Pyramis simili hiatu congruit, ad figuram undique, claudendam. Hinc Octaedron.
Quinque Trigoni, singulis angulis congruentes, efficiunt 10 teritas, quod est minus quam 12 tertia, fitque aptatis denis & denis lateribus ad angulum communem, Pyramis basi quinque latera, cujus anguli ad basin, ut & ipsi fiant quinque planij, oportet binis in ea basi planis, alos ternos angulos planos, & sic decem, illos alios quindecim, congruere, totidemque porrigi altrorsum: quae summa tnginta planorum, est decem Trigonorum; ex quibus in medio Zona vel columna fit, hians infra ut supra, figura quinquangulari; in quam congruit alia Pyramis pentahedrica; ut figura claudatur undique. Hinc Icosaedron.
Sic est transactum cum Trigonii meris.
Tres Tetragonici anguli, sunt tres recti, minus quam quatuor recti plani: congruunt ergo ad formandum angulum solidum, hiantque coagmentati tetragoni, tribus rectis planis angulis, & vicissim extant tres anguli trium illorum planorum: tres igitur alij Tetragoni, singulis angulis in unum solidum congruentes, apti sunt & congrui, qui suis extantibus illos hiatus expleant, suisque hiatibus illos extantes recipiant. Hinc Hexaedron vel Cubus.
Quatuor Tetragonici aequant quatuor rectos, quare per XVl non solidum quid formant. Sic est transactum cum Tetragonis meris.
Tres Pentagonici anguli sunt 13 quintae unius plani recti, minus quam 20 quintae seu quatuor recti. Congruunt igitur ad unum solidum formandum; quid si Pentagonus unus in basi cingatur hoc pacto quinque alijs, figura sursum hiat 5, angulis planis pentagonicis, habetque extantes quinque angulos planos pentagonicos. Alia igitur ex adverso figura est struenda, huius similis; & quini aiterutrius anguli plani extantes congruent in quinos reliquae hiatus, & vicissim. Hinc nascitur Dodecahedron. Transactum sic est cum Pentagonis meris, & simul cum figuris omnibus unius solius speciei coaptandis: quia tres Hexagonici ter XVI. non assurgunt ad solidandum.
Haec sunt illa corpora quinque, quae figuras mundanas appellare sunt soliti Pythagoraei & Plato, & Euclidis commetator Proclus: quae quomodo fuerint applicatae corporibus mundanis, in praeambulo lib. I. dixi, incertum esse. Communis quidem persuasio est,ducta ex Aristotele, Philosophos illos ad quinque simplicia Corpora Mundi respexisse secundum quinarium, numerum harum figurarum, scilicet ad quatuor Elementa , Ignem, Aerem, Aquam, Terram , & ad sic dicam, Quintam Essentiam, seu Materiam coelestam; comparatis figurarum proprietatibus, cum simplicium illorum corporum affectionibus.
Nam in Cubo rectitudo super basi quadrata stabilitatis quandam adumbratione habet, quae eadem proprietas est & Materae terrestris, gravitatis momentis ima petentist: cum etiam totus Terrae globus vulgo credatur in medio Mundi quiescere. Vicissim Octahedri congruus est situs aspectui, si is duobus opposit is angulis velut in torno suspendatur, inter quos medio pracise loco est latens quadrilaterum, dividens corpus figurae in duo aequalia, sicut globum a duobus polis suspensum dividit maximus circulus: haec est quaedam imago mobiiitatis, uti aer est elementorum mobilissimum & celeritate & Varietate plagarum.
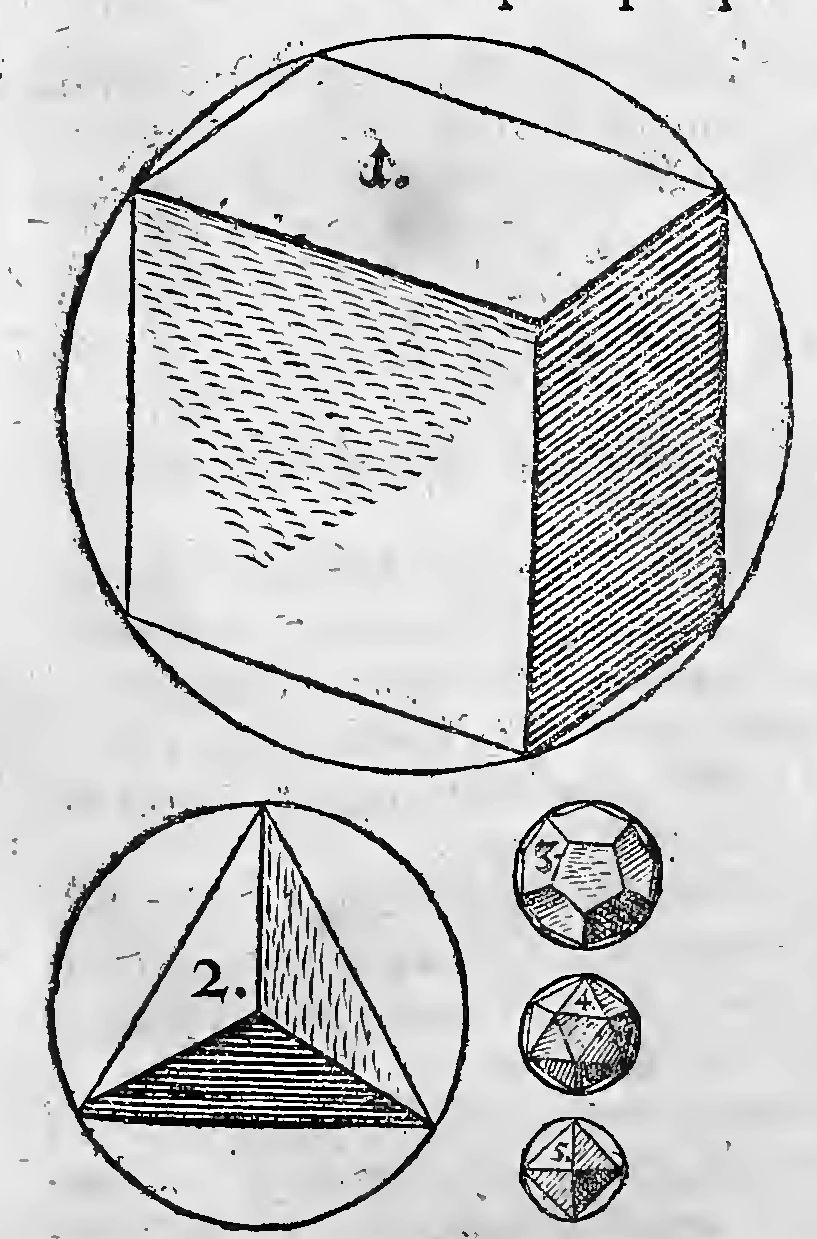
ln Tetrahedro paucitas planorum fignare videtur siccitatem ignis, cum definitio sit siccorum, suis contineri terminis; in Icosaedro vicissim multitudo planorum signare videtur humiditatem aquae, cum desiniatur humiditas, alienis contineri terminis; est quippe paucitas, propriorum, multitudo, adscitorum & alienorum indicium. Et aliter etiam, Trigonus planus, est Tetrahedri proprius, quia tota Tetraedrica figura est trigonus solidus: idem vero Trigonus, est Icosaedri non proprius, sed mutuatitius, quia Icosaedri soliditas, Pentagoni similis est, non Trigoni. Rursum in Tetraedri acumine ab una basi surgente, vis Ignis penetrativa & divisoria videtur adumbrata esse, in Icosaedri obituso & quinquelineari angulo, vis impletoria humorum, hoc est vis humectandi; in Tetraedri parvitate & macilentia, natura ignis; in Icosaedri mole globiformi, natura aquae, & quaedam velut figura guttae: in Tetraedro plurimum est superficiei, minimum corporis; in Icosaedro moles corporea multo major quam superficies: quemadmodum in Igne forma praecellit, in Aqua materia.
Dodecaedron vero relinquitur corpori caelesti, habens eundem planorum numerum, quem Zodiacus caelestis figurarum; demonstraturque reIiquarum figurarum capacissima: quemadmodum & coelum capit omnis.
Haec Analogia etsi plausibilis est; non quidem Aristoteli (qui cum creatum esse Mundam negaret, vim in figuris quantitativis Archetypaiem agnoscere non potuit; quippe quaesine Architecto nulla illis inest ad faciendum aliquid corporeum) sed mihi, Christianusque omnibus, qui fide tenemus, Mundum, cum antea non esset. A Deo cratum esse, in pondere mensura & numero, scilicet Ideis ipsi coaeternis: etsi inquam plausibilis est in genere haec analogia; tamen sic in specie informata, nulla necessitate continentur; & patitur instantias, non tantum ob quarundam proprietatum discrepantiam in eadem analogia; sed etiam on majorem convenientiam Dodecaedri & Icosaedri cum Igne: denique quia de Elementorum nummero & quiete Telluris, disputatio multo majore est, quam de harum figurarum numero.
Quod si hic substitterunt Pythagorei, non reprehendo in hac parte Ramum, non Aristotelem, quod hanc analogiam disputationibus convulsam rejecerunt. At ego ante annos viginti quatuor, longe aliter haec quinque corpora in fabrica mundi indagavi; dixique in praeambulo libri I. mihi videri consentaneum, eandem doctrinam etiam veterum fuisse, sed occultatam more sectae. Cum enim habeat Astronomia Copernicana, seu veteris Aristarchi Samij Pythagorici, dispositionem Mundi mobiiis talem; ut sint in eo sex Orbes seu curricula, circa corpus solis in centro immobile circumducta, magnisque & inter se inaequalibus intervallis dirempta, Saturni extimi, deinde Jovis, dein Martis, inde Telluris cum Luna, tum Veneris, denique Mercurij intimi: cumque figurarum harum quinque, propria & essentialis sit inscriptio in Sphaericam superficiem, cum angulis , & circumscriptio circa Sphaericam superficiem, cum centris planorum; adeoque cuilibet figurae certum sit intervallum inter suos binos orbes: nihil plausibilius videri potuit, quam sex illorum caelestium orbium intervalla quinque, ex quinque figuris esse desumpta a Creatore; hoc ordine ut cubus mente concipiatur inter Orbes Satutni & Jovis, Tetraedron inter Jovis & Martis, Dodecaedron inter Martis & Terrae, Icosaedron inter Telluris & Veneris, Octaedron inter Veneris & Mercurij.
Haec distributio numeris explorari potest, necessitatem infert, corporum numerum non conquirit anxie,sed inventum occupat; denique sic est instructa, ut ab bis annis viginti duobus non tantum nullum invenerit oppugnatorem, sed etiam ipsos Rami inconsiderati Magistri & Euclideoma stigis discipulos pertraxerit; hodieque tam multos pertrahat, ut jam dudum secundam editionem flagitaverint Mathematici. Sed de hac re pluribus agere, non est hujus secundi libri; inveniet lector infra libro quinto plura, aliqua etiam in Epitomes Astronomiae libro IV. ubi ortus harum quinque solidarum figurarum genuinus explicatur metaphysice: nam ille per angulationes, non vere ortus est, sed ortas conjequitur, ut natura a posteritis quid.
XXVI. Propositio.
Addi possunt congruentijs perfectissimis regularibus, duae etiam aliae congruentiae, stellarum duodecim planarum Pentagonicarum: & duae semisolidae, stellarum Octangulae , & Decangulae.
Claudunt enim pentagonicae solidas figuras aculeatis undique: quarum una sit duodecim angulorum quinquelinearium, altera viginti angulorum trilinearium: illa trinis angulis insistit; haec quinis simul; illa pulchrius super angulum erigitur; haec rectius sedet; incumbens in quinos. In his etsi forinsecus non apparet regulare planum, sed ejus loco Triangulum aequicrurum Pentagonicum; quina tamen hujusmodi semper in unum idemque planum competentia, occultum sub soliditate quinquangulum, veluti cor suum circumstant; faciuntque cum eo dictam stellam pentagonicam, seu Germanico Idiomate, pedem Truttae, Theophrasto Paracelso signum sanitatis, Idea corporis quodammodo eadem est, quae sui Plani. Nam ut in hoc, sc.. in stella quinquangula, binorum semper triangulorum latera in unam rectam competunt, quae parte sui interiore fit basis uni exteriori triangulo, latus vero intimo quinquangulo: sic in solido, semper quinorum solidorum angulorum Triangula singula aequicrura; competunt in unam planitiem, quorum quinque triangulorum seu stellae intima medulla & cor, quinquangulum, fit basis in una super stantis anguli solidi,: vel in altera, sui stantium quinque solidorum. Est autem tanta cognatio figurarum harum, unius cum Dodecaedro, alterius cum Icosaedro: ut videantur hae, praesertim Dodecaedron, trunca quodammodo& mutila, si cum illis aculeatis comparentur.
Octangulae vero & Decandulae stellae, lateribus suorum radiorum, quae semper in primo & quarto, duobus transitis, congruunt in unam rectam, binae semper & bina congruunt, faciuntque cubum illae quendam, hae Dodecaedron quoddam, non angulatas sed auriculatas figuras: quia duobus planis angulis coaptatis, hiatu fieri necesse est, qui claudi noh potest. Ergo p XI, semisolida tantum est congruentia.
Perfectissima dicuntur congruentiae, illae solidae, hae semisolidae, quia ipsis competit Vl, definitio hujus lib. quoad soliditatem: planitiebus vero ipsis competit definitio figurae perfectae, quae est libro I. secunda, sunt sc. secundario perfectae. Nec absurde dicimus, semisolidam perfectissimam, quia innuimus inchoari aliquid; qui non IX vel X sed cui VI Def. competeret si perfici posset.
XXVII. Propositio.
Congruunt etiam ad solidandas figuras, semiregulares figurae scilicet Rhombi plani, perfectissime, idque tantum bis.
Nam ex duodecim planis Rhombis, certae proportionis Diagoniorum, fit Rhombus solidus, figura cellulae Aptariae, quantum ad latera sex, & fundum triangularem solidum: sex enim Rhombi congruentes sic, ut obtusi obtusis, acuti acutis applicentur, tres habent obtuangulos hiatus, tria etiam paria acutorum extantia supra, totidemque infra. Congruunt igitur trium utrinque Rhomborum, obtusis conjunctorum ternae eminentiae, in hiatus, recipiuntque suis hiatibus illorum eminentias.
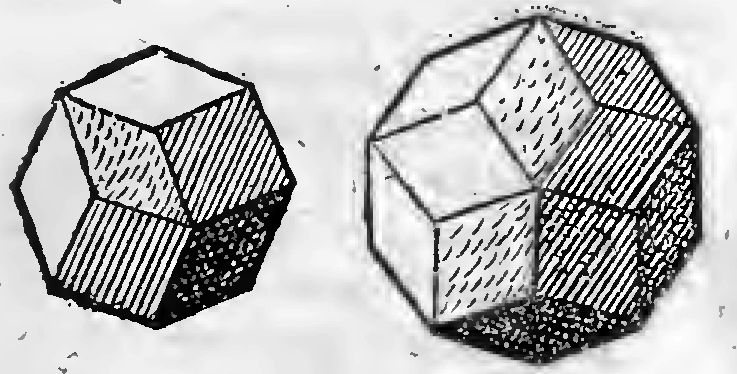
Sic triginta Rhombi plani, proportionis Diagonorum alterius, faciunt Rhombum solidum Triacontaedricum Quini enim & quini Rhombi angulis acutis conjuncti, ad effigiandos duos solidos ex oppositis plagis stantes, cum hient apud obtusos conjunctos; quinorum & quinorum Rhomborum obtusis alijs, implent hiatus: denique in utriusque veluti testae medio, Zona ex decem Rhombicis composita circumit, conjungens utramque testam.
Non esse vero plures perfectas Rhomborum congruentias; sic probatur. Sunt enim duo anguli plani Rhombici acuti, duo obtusi; quorum semper acutus unus & unus obtusus faciunt duos rectos: nec plures tribus obtusis congruunt, ne superent quatuor rectos. Quod siergo tres solitum acutos conjunxeris, fit ut in Cubo , Hexahedron Rhombicum, cum duobus solum solidis acutis, longissime distantibus; caeteri solidi in medio corporis non tantum distant: non servantur igitur leges definitionis VIII, quae non admittit duos solos angulos in eadem sphaera. Praeterea ex sex solidis obtusis quilibet clauditur a duobus obtusis planis & uno acuto; quae irregularitas rursum est contra definitiones. Ergo non tres tantum plani acuti coire debent. At aeque sex acuti, totidem scilicet Rhomborum, coeunt. Si enim singuli habent quantitatem 2 tertias unius Recti, obtusi habebunt duplam quantitatem, scilicet 4 tertias: & sic tam tres obtusi, quam sex acuti formabunt 4 Rectos, nec vel illi vel hi formabunt angulum solidum sed sternent continuam planitiem, ut in figura G. Sin autem acuti minores sumantur, obtusi maiores erunt, & tres superabunt quatuor rectos. Ergo duae tantum sunt per sectissimae Rhombicae congruentiae: una , in qua quatuor acuti anguli Rhombici coeunt in solidum; altera, in qua quinque: quibus tamen associatur Cubus, tanquam Rhomborum omnium principium, quia planum ipsius est laterum aequalium quatuor, ut Rhombicorum.
XXVIII. Propositio.
Perfectae in solido congruentiae gradus inferioris, species sunt tredecim; ex quibus tredecim oriuntur Archimedea Corpora.
Cum enim misceantur in hoc gradu figurae diversae, quare per propos. XXI. Miscebuntur aut duarum aut trium specierum figurae. Quod si duarum, tunc inter eas vel sunt Trigoni vel non sunt.
Igr ex Trigonis & Tetragonis fiunt solida tria, quibus quidem def. IX. competat. Nam illa rejicit formas hasce tres, in quibus solidum angulum claudunt, cum uno Tetragonico plano angulo, tam duo, quam tres plani Trigonicis; aut cum duobus Tetragonicis, unus Trigonicus; quia in primo casu unus solus Tetragonus est, fitque dimidium Octraedri & anguli solidi sunt diversiformes: in secundo duo soli Tetragoni, in tertio duo soli Trigoni: quae p. X, sunt imperfectae congruentia. Restant ergo modi hi, in quibus angulum solidum claudunt 1 lani, Primum, quatuor Trigonici & unus Tetragonicus. Sunt enim minores 4 rectis. Congruunt igitur sex Tetragoni & Triginta duo (id est 20 & 12.) Trigoni, & fit figura Triacontaoctahedrica, quod appello Cubum simum. Hic in schemate sequenti pictus est Numero 12.
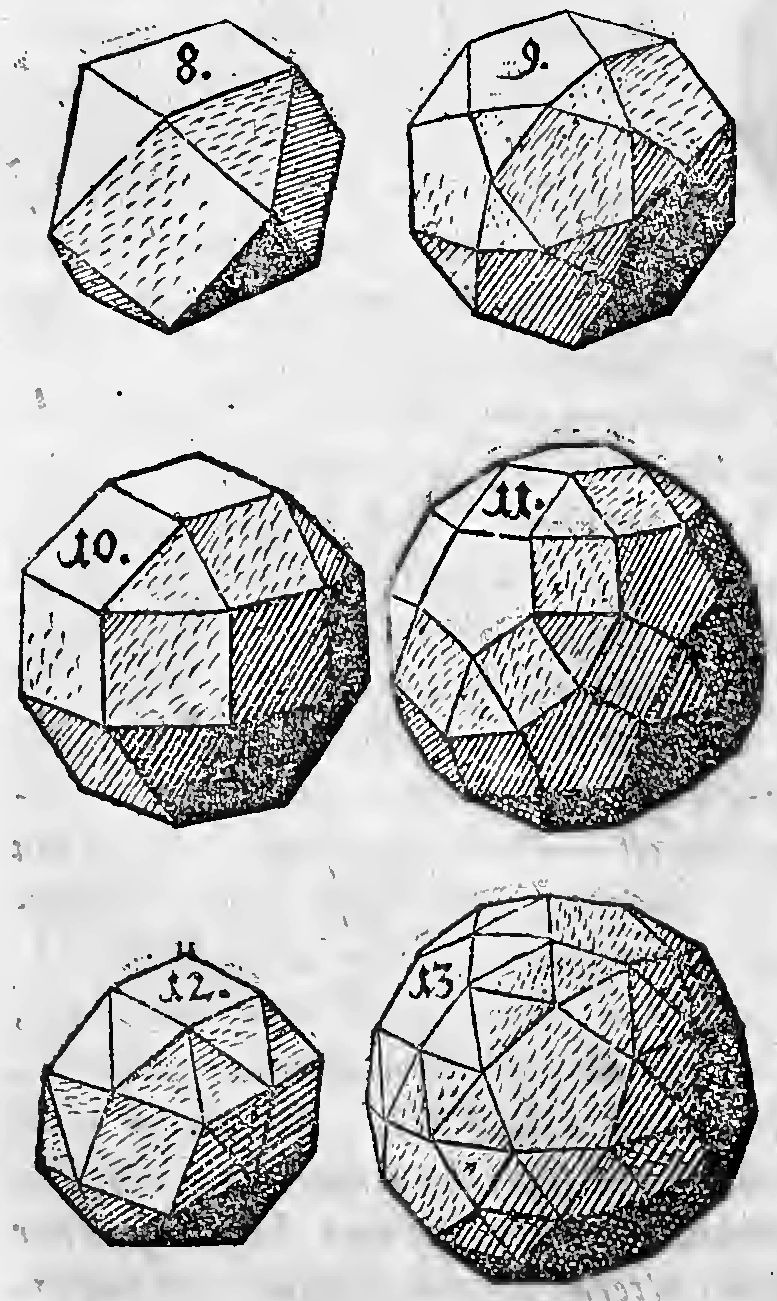
Quinque enim Trigonici plani & unus Tetragonicus superant quatuor rectos, cum debeant ad solidu, claudendum esse minores quatuor rectis, per XVI. Sic etiam quatuor Trigonici & duo Tetragonici. Tres vero Trigonici & duo Tetragonici faciunt quatuor rectos.
Secundo duo Trigonici & duo Tetragonici minus habent quatuor rectis. Hic igitur congruunt octo Trigoni & sex Tetragoni ad formandum unum Tesareskadecaedron, quod cuboctaedron appello. Pictum est hic num: octavo. Duo vero Tetragonici cum tribus Tetragonicis superant 4 rectos.
Tertio unus Trigonicus & tres Tetragonici minus habent 4 rectis Hic ergo congruunt octo Triangula & octodecim & (id est 12 & 6) quadrangula, ad unum Icosihexaedron, quod appello sectum Rhombi Cuboctaedricum: vel Rhombicubooctaedron. Pictus est hic numero 10.
In his igr tribus sunt Tetragoni juxta Trigonos: sequitur ut & Pentagonicos ijs seorsim associemus. Quinque plani Trigonici juxta unum Pentagonicum non stant, quia neque juxta minorem eo, Tetragonicum, stare poterant. Quatuor ergo Trigonici, cum uno Pentagonico, minus efficiunt 4 rectis, & congruunt octoginta (id est 20 & 60) Trigoni, cum duodecim Pentagonis, ad formandam Ennenecontakaedyhedron, quod appello Dodecaedron simum: Pingitur hic numero 13. Et in hoc ordine simorum, Icosaedron posset esse tertium, quod est quasi Tetraedron simum.
Tres planos Trigonicos si uni Pentagonico associaveris, fit quod supra, ut duo solum Pentagoni veniant in solidum; & si duos Trigonicos uni pentagonico, venit unus solus Pentagonus in solidum: fitque illic Zona vel columna media; hic Pyramis, partes Icosaedri: nec anguli solidi sunt hic ejusdem speciei, quia unus ambitur, ut in Icosaedro, quinque Trigonicis. Et transactum est cum unico Pentagonico.
At tres Trigonici cum duobus Penthgonicis plus efficiunt 4 rectis. Transactum igitur est cum tribus Trigonicis in societatem Penthgonicorum adsciscendis.
Duo Trigonici cum duobus Pentrigonicis minus efficiunt 4 Rectis. Congruunt igitur viginti Trigoni & duodecim Pentagoni in unum Triacontakaedyhedron, quod appello Icosidodecahedron. Pingitur hic Numero 9. Cum uno Pentagonico duos Trigonicos jam rejecimus, Transactum igr est cum duobus Trigonis.
Unus Trigonicus cum tribus Pentagonicis plus quam 4 rectos efficit, cum duobus vero per XXIII. Nihil regulare, quia Pentagonus est figura imparilatera. Sicque transactum est cum Pentagonis in societate Trigonorum.
Trigonici quatuor cum uno Hexagonico, & duo tum duobus Hexagonicis implet planitiem; at tres cum duobus sunt majores 4 rectis, cum uno Hexagonico duos solos Hexagonos in figuram recipiunt; rejecis igr tribus Trigonicis, duo sunt aequales uni Hexagonico, quare rejecti per XXII. Restat ut unus Trigonicus cum duobus Hexagonicis copuletur: Itaque congruunt quatuor Trigoni cum quatuor Hexagonis in unum Octaedron, quod appello Truncum Tetraedron; Pingitur Numero 2 fol. sequenti.
Trigonici quatuor cum uno Heptagonico & majoribus, superant 4 rectos; nulla igitur porro mentio facienda est quatuor Trigonicorum: nulla etiam trium, ob causas saepe allegatas: duo vero cum figurarum Hexagono majorum binis planis, superant 4 rectos: nulla igitur neque duorum porro est facienda mentio; cum binis planis figurae. Majoris, nec duorum cum uno plano figurae majoris, quia illi superantur ab hoc, quod rejectum est ax XXII. Restat examinandus hic casus, cum unus Trigonicus duobus planis figurae majoris Hexagona copulatur: atqui cum duobus Heptagonicis rejicitur per XXlII. ut & cum omnium imparilaterarum duobus: cum duobus vero Octagonicis, sit corpus, in quo cogruunt octo Trigoni & sex Octogoni in unum Tessarakaedecahedron, quod appello Cubum Truncum. Ejus figuram habes signatam Num. 1 fol. seq. Cum duobus Decagonicis, fit corpus, in quo congruunt viginti Trigoni & 12 Decagoni, in unum Triacontakaeidyhedron, quod Appello Truncum Dodecaedron. Id signatum est inter figuris sequerites Num. 3. Cum duobus Dodecagonicis impletur planities, nec sit solidus angulus, multoque minus cum majoribus. Et transactum est in universum cum Trigonis: in dualitaite quidem specierum.
Cum ergo inter binas planorum species non amplius sunt Trigoni: minima porro figura erit Tetragonus. Atqui Tetragonici tres, cum uno majoris plani angulo, superant 4 rectos: duo vero Tetragonici cum uno majoris, non tolerantur, ob definitionem IX, quia majoris speciei figurae tantum duae reciperentur in solidum. Unus igr Tetragonicus cum duobus Pentagonicis rejicitur per XXIII: cum duobus Hexagonicis coit, & congruunt sex Tetragoni cum octo Hexagonisin unum Tesserakadecadedron, quod Appello Truncum Octaedron, Pingitur numero 5 sequentis schematis. Unus Tetragonicus cum duobus Heptagonicis alijsque imparilaterarum rejicitur, per XXIII. Cum duobus Octagonicis, planum locum imples: cum majoribus etiam superat 4 rectos; nec assurgit ad solidum angulum formandum. Ita transactum est cum Tetragono, cum duae sola deberent esse planorum species.
Duo Pentagonici cum uno Hexagonico aut quocunque alio unico rejectitium quid inchoant, per XXIII, quod supra etiam de Trigonico & Tetragonico cum binis Pentagonicis usurpavimus. Insuper cum uno Decagonico planitiem sternunt, nec cum illo aut majoribus assurgunt in soliditatem.
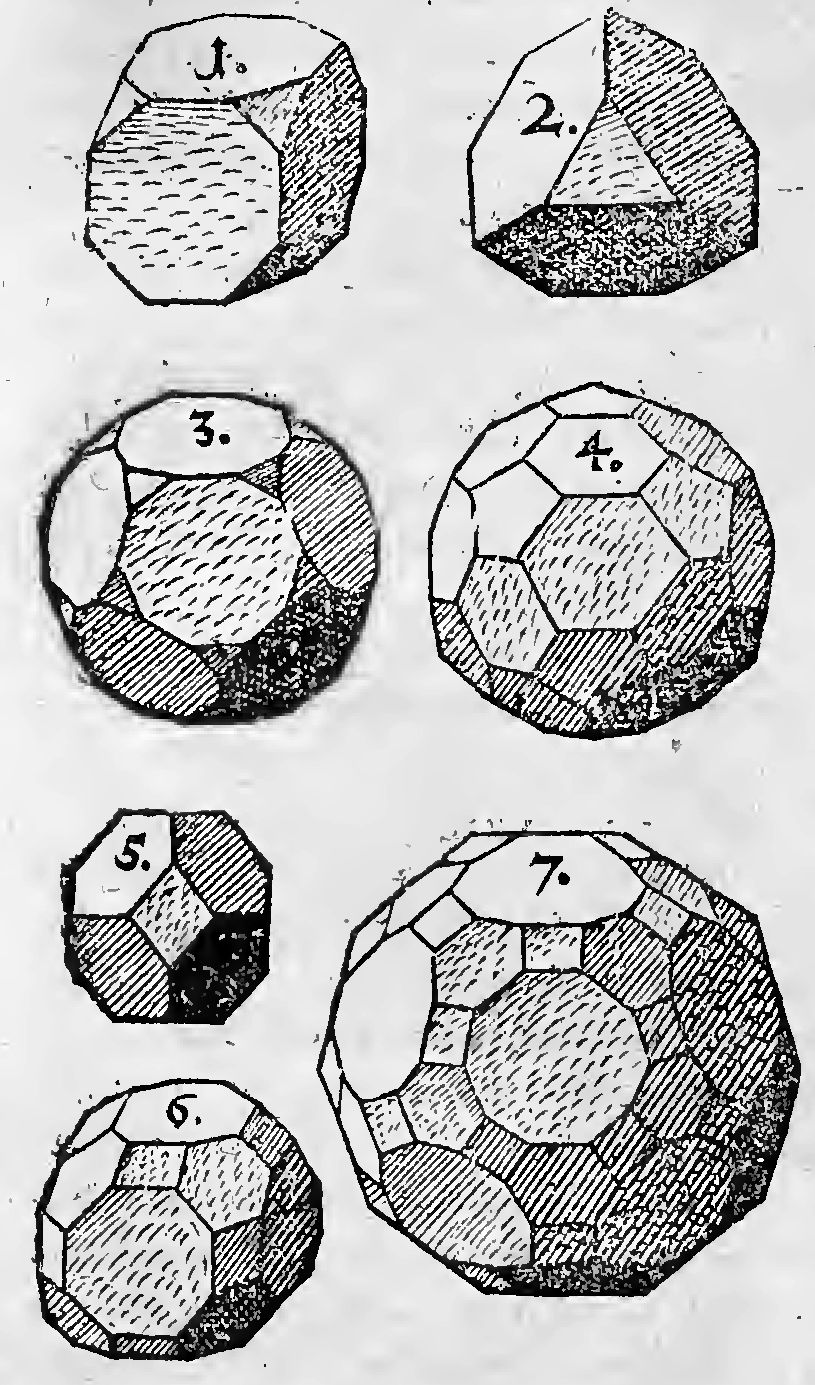
Unus ergo Pentagonicus cum duobus Hexagonicis minus facit 4 rectis; & congruunt duodecim Pentagoni cum viginti Hexagonis in unam Triacontakaedyhedron, quod appello Truncum Icosihedron. Formam habes signatam numero 4 . Nec plura expectanda a Pentagono. Nam unus Pentagonus cum duobus Heptagonicis jam superat 4. rectos.
Hexagonicus cum duobus alijs implet planitiem, cum majoribus superat 4 rectos. Itaque hic finis est mixtorum ex duabus speciebus.
Quod si trium specierum Plana concurrere possunt ad unum angulum solidum: Primum anguli duo plani, unus Tetragoni, alter Pentagoni superant 2 rectos; majores his, multo magis: tres vero Trigonorum trium, aequant 2 rectos: nequeunt igr tres Trigonici admitti, ne summa omniis superet 4 rectos. Duo verb Trigonici cum uno Tetragonico & uno Pentagonico vel pro eo Hexagonico, aut quocunque majori, rejiciuntur, per pr. XXlII. quia Trigonus imparilatera figura cingi deberet Tetragono & Pentagono, vel pro eo Hexagono &c.
Unus igitur Trigonicus eum duobus Tetragonicis & uno Pentagonico, minus efficiunt 4 rectis, & congruunt 20 Trigoni cum 30 Tetragonis & 12 Pentagonis, in unum Hexacontadyhedron, quod appello Rhombicosidodecaedron, seu sectum Rhombum Icosidodecaedricum. Pingitur num. 11. Fol. antecedentis.
Unus Trigonicus, duo Tetragonici, cum uno Hexagonico, aequant rectos quatuor; cum uno majori, superant; nec ad solidum assurgunt. Mittamm igitur duos Tetragonicos.
Unus Trigonicus, unus Tetragonicus, & duo Pentagonici superant 4 rectos; multoque magis si bini majores plani anguli admiscerentur. Definiunt igitur misceri anguli plani quaterni ad formandum unum solidum; definit ergo & Trigonus ingredi mixturam triplicem. Nam unus Trigonicus, unus Tetragonicus & unus pentagonicus, aut quicunque alius hujus loco, rejiciuntur per XXIV, quia trigonus est imparilatera figura.
Cum igitur porro sint tres solum anguli plani: nulla inter figuras toleratur imparilatera, per eandem XXIX.
Tetragonicus igitur, cum Hexagonico & Octagonico minimis,minus faciunt 4 rectis & congruunt 12 Tetragoni, 8 Hexagoni, & 6 Octogoni, in unum Icosihexaedron, quod appello truncum Cuboctaedron: non quod truncatione nasci possit; sed quia simile est truncato Cuboctaedron. Pingitur num. 6.
Tetragonicus cum Hexagonico & Decagonico, minus 4 rectis efficiunt: & congruunt 30 Tetragoni, 20 Hexagoni & 12 Decagoni, in unum Hexacontadyhedron, quod appello truncum Icosidodecaedron, simili de causa ut proximum. Pingitur num. 7.
Si pro Decagonico succedat in societatem Dodecagonicus; implentur 4 recti, nec fit solidum; sic etiam si pro Hexagonico succedat Octogonicus, & aliquis, Octogonico major, sit tertius: superantur 4 recti: nec minus, si absit Tetragonicus, & socientur tres distinctarum figurarum parilaterarum majores. Igitur stat omnis Archimedeorum familia intra num. 13. Quod erat demonstrandum.
XXIX. Consectarium.
Figurae congruae sunt in universum duodecim, octo Radicales seu Primae, & quatuor auctae seu Stellae.
| 1. Trigonus | 7. Dodecagonus |
| 2. Tetragonus. | 8. Icosigonus |
| 3. Pentagonus | 9. Stella Pentagonica |
| 4. Hexagonus | 10. Stella Octogonica |
| 5. Octogonus | 11. Stella Decagonica |
| 6. Decagonus | 12. Stella Dodecagonica |
Gradus congruentiae distincti sunt. In primo sunt Trigonus & Tetragonus, quia congruunt tam in solido, quam inplano, tam singularum specierum inter se, quam junctarum, & cum alijs.
Secundo gradu consitunt Pentagonus cum stella sua. Nam congruunt & singularum specierum inter se, in solido: & tradunt mutuas operas in plano: sed potior est Pentagonus, quia congruit etiam cum alijs nonnullis tam in plano, quam in solido.
Tertius est Hexagoni, quia figurae hujus speciei congruunt in plano, cum alijs vero tam in solido quam in plano.
Quartum gradum tenent Octogonus & Decagonus cum stellis suis. Nam Radicales illea, cum alijs nonnullis congruunt in dolido, stellae. vero cum figuris singularum specierum quadamtenus: in plano vero omnes quatuor congruunt cum alijs, magis tamen varie magisque perfecte Octogonica secta.
Quintus gradus habet Dodecagonum cum stella sua; quia in solido quidem minime, at in plano multifariam congruunt cum aiijs; in solido igitur sola magnitudine impediuntur. Causa planitiei praeferenda est haec secta gradus quarto.
Ultimus gradus est Icosigoni, quia is non nisi in plano, nec nisi cum alijs, & cum illis ipsis quoque imperfecte congruit.
Quod si solam consideremus Planitiem, Ordo figurarum erit iste: 1. Hexagonus. 2. Tetragonus. 3. Trigonus. 4. Dodecagonus. 5. Stella ejus. 6. Octogonus. 7. Stella ejus, 8, Pentagonus. 9. Stella ejus. 10. Decagonus. 22 Stella ejus. 12. Icosigonus.
Omnes aliae figurae sunt incongruae proximus tamen congruentiae est Pentekadecagonus, quia incipit congruere cum alijs in plano; at excluditur per XXlII. Quo minus ut Icosigonus, cingi undique aequaiiter possit. Post illum est figura 16 laterum & similes, quae plane non congruunt cum regularibus alijs; impediente magnitudine angulorum. At Heptagonus & similes longe alia, ratione sunt incongruae figurae, quia nec toti anguli, nec partes angulorum aliquotae, propriae figurarum, cum alijs regularibus congruunt.
Ita in tribus per se demonstrabilium classibus definit congruentia, in Octogono, Dodecagono, Icosigono, in quarto spurio ne incepit quidem. Haec libro IV in delectu Aspectuum suum usum habent.
XXX. Consectarium.
Ex his genuinum discrimen apparet inter demonstrationem & congruentiam figurarum causa latitudinis.
Nam 1. Demonstrationis propriae gradus ultra Octogonum, Decagonum, Dodecagonum, in figuras duplorum laterum in infinitum excurrunt: Congruentia in Octogono, Icosigono, Dodecagono subsistit. 2. Pentagonus cum stella sua, causa demonstrationis & scientiae, est ignobilior Dodecagono: causa congruentiae in solido, est multo nobilior. 3. Octogonus ibi sequitur Pentagonum, hic antecedit. 4. Hekkadecagonus ibi erat potiore loco, quam Icosigonus: & tamen illa est figura incongrua, haec congrua quadamtenus. 5. At in Pentekadecagono pulchra est rei utriusque convenientia, analogiam servans eandem: quia inter demonstrationes nulla illi obvenit propria, sed accidentaria saltem; inter vero congruentias nulla consummata, sed aliqua saltem inchoata, nec totam figuram occupant. Haec infra libro III, in ortu & usu semitonij sunt notanda.
Finis Libri II.
© Rainer Stumpe, URL: www.rainerstumpe.de/
Datenschutzerklärung