Des Apollonius von Perga sieben Bücher über Kegelschnitte

Des
Apollonius von Perga
sieben Bücher über Kegelschnitte

nebst dem durch Halley wieder hergestellten
achten Buche.

Deutsch bearbeitet von
B. Balsam.

Dabei ein Anhang, enthaltend:

Die auf die Geometrie der Kegelschnitte bezüglichen Sätze aus Newtons "philosophiæ naturalii principia mathematica."

Berlin, 1861.
Verlag von Georg Reimer.

Zweites Buch des Apollonius von Perga über Kegelschnitte.

Apollonius grüsst den Eudemos.

Es freut mich, wenn Du wohl bist; ich befinde mich ziemlich nach Wunsch. Ich habe meinem Sohn Apollonius das zweite Buch der Kegelschnitte, das ich geschrieben habe, übergeben, dass er es Dir bringe. Du wirst dasselbe sorgfältig durchlesen und denen mittheilen, die Dir dessen würdig scheinen werden. Auch dem Geometer Philonidas, den ich in Ephesus Dir zum Freunde gemacht habe, wirst Du dasselbe zu lesen geben, wenn er einmal nach Pergamus kommt. Sorge, dass Du gesund bleibst.

Lehrsatz 1. Wenn auf einer Tangente im Scheitel einer Hyperbel vom Berührungspunkt aus nach beiden Seiten gleiche Stücke abgeschnitten werden, welche einzeln gleich der mittleren Proportionale zwischen dem halben Latus transversum und dem halben Latus rectum sind, so treffen die Linien, die vom Mittelpunkt nach den erhaltenen Endpunkten gezogen werden, mit der Hyperbel nicht zusammen.

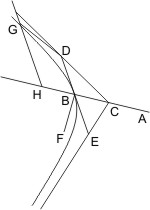
Sei eine Hyperbel mit dem Durchmesser AB, dem Mittelpunkt C und dem Latus rectum BF gegeben, und werde auf der im Scheitel B gezogenen Tangente nach jeder Seite zu ein Stück, BD nach der einen, BE nach der andern Seite, abgeschnitten, dessen Quadrat gleich dem vierten Theile des Rechtecks aus AB und BF ist, und die Linien CD, CE gezogen, so wird behauptet, dass diese Linien mit der Hyperbel nicht zusammentreffen.
Beweis. Träfe die verlängerte CD die Hyperbel in G, so ziehe man die Ordinate GH, dann wäre
1. GH² : HB · HA, d. h. GH² : HC² - CB² = BF : BA,
oder wenn das zweite Verhältnis mit AB ⁄4 erweitert und 1 ⁄ 4 · BA · BF = BD², 1 ⁄ 4 · BA² = CB² gesetzt wird,
1. GH² : HC² - CB² BD² : BC².
Es ist aber aus der Aehnlichkeit der Dreiecke CHG, CDB
1. GH² : HC² = BD² : BC².
Also müsste HC² = HC² - CB² sein, welches unmöglich ist, und folglich kann die verlängerte CD mit der Hyperbel nicht zusammentreffen.
Lehrsatz 2.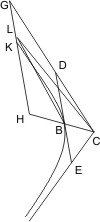 Unter denselben Voraussetzungen ist zu zeigen, dass von C aus in den Winkelraum DCE keine andere Asymptote gezogen werden kann.
Wäre CL eine solche Asymptote, so ziehe man vom Scheitel B mit CD eine Parallele, bis sie CL in L trifft; ferner von L parallel mit DB die Ordinate LH, welche die verlängerte CD in G, die Hyperbel in K schneidet. Nun ist nach dem, was in § 1 bewiesen:
1. KH² : HC² - CB² = GH² : HC² , oder
2. GH² - KH² : CB² = GH² : HC² = DB² : CB²;
also müsste GH² - KH² = DB² sein, was unmöglich ist, denn GH² - KH² = (GH - KH) · (GH + KH) = GK · (GK + 2 ·, KH) und GK > GL, aber GL = DB. Mithin ist bewiesen, dass ausser CG und GM keine andere Asymptote in den Winkelraum GCM gezogen werden kann.
Lehrsatz 3. Wenn eine gerade Linie eine Hyperbel berührt, so schneidet sie beide Asymptoten und ihr Berührungspunkt ist die Mitte des Stücks zwischen den Asymptoten; das Quadrat ihrer Hälfte aber ist gleich dem vierten Theil des zum Durchmesser nach dem Berührungspunkt gehörigen Rechtecks.

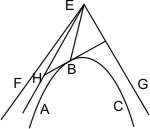
Sei ABC eine Hyperbel, E ihr Mittelpunkt, EF, EG die Asymptoten und in B eine Tangente gezogen. Träfe diese nun eine Asymptote EF nicht, so könnte man auf ihr nach der Seite dieser Asymptote zu ein Stück BH gleich der mittleren Proportionale zwischen dem halben Latus rectum und dem halben Latus transversum abschneiden, dann wäre nach § 1 EH eine andere Asymptote, was nach § 2 unmöglich ist. Also trifft die Tangente jede Asymptote und es ist das Quadrat jedes Stücks zwischen Berührungspunkt und Asymptote gleich dem vierten Theil des zum Durchmesser gehörigen Rechtecks.
Aufgabe 1. Wenn ein Winkel und zwischen seinen Schenkeln ein Punkt gegeben ist, eine Hyperbel zu construiren, die durch den Punkt geht und die Schenkel des Winkels zu Asymptoten hat.

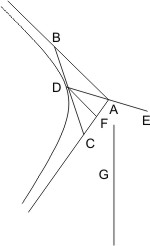
Sei BAC der Winkel, D der Punkt zwischen seinen Schenkeln; man soll eine Hyperbel construiren, die durch D geht und AB, AC zu Asymptoten hat. Man ziehe DA und verlängere es über A bis E, so dass AE = AD ist; ferner ziehe man von D, parallel mit BA, die Linie DF, welche AC in F schneidet, mache AF = FC und ziehe CD, welche AB in B trifft. Endlich nehme man zu DE und BC die dritte Proportionale G und beschreibe für den Durchmesser ED das Latus transversum ED, das Latus rectum G und den Ordinatenwinkel BDA eine Hyperbel, so ist dies die verlangte.
Weil AF = FC und FD parallel AB, ist BD = DC, und da BC die mittlere Proportionale zwischen Latus rectum und transversum, ist es BD zwischen den Hälften dieser Linien, also sind AB, AC Asymptoten der Hyperbel.
Anm. Commandinus sagt, dass diese Aufgabe nicht vom Apollonius, sondern vom Eutocius oder irgend einem andern herrührt; 1) weil Archimedes im 4. Satz des 2. Buchs über Kugel und Cylinder sagt: ώς δἑ δεῖ διἀ τοῦ δοϑϑνος σημεἰον περί τἀς δοςείσας ἀσνμπτώττνς γράψαι ὑπερβολήν, δείξομεν ούτως, ἐπειδή οὐχ αὐτόςεν χεῖται έν τοῖς χωνιχοῖς στοιχείοις. 2) Weil Pappus unter den Lemmen, die er zum fünften Buch giebt, diese Aufgabe mit derselben Auflösung behandelt.
Lehrsatz 4. Wenn ein Durchmesser einer Parabel oder Hyperbel eine Sehne halbirt, so ist die Tangente im Scheitel dieses Durchmessers parallel der halbirten Sehne.

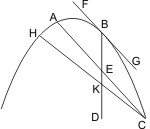
Sei ABC eine Parabel oder Hyperbel mit dem Durchmesser DBE, FBG eine Tangente im Scheitel B; und werde die Sehne AC vom Durchmesser DB im Punkte E halbirt, so wird behauptet, dass AC parallel FG ist. Wäre dies nicht der Fall, so ziehe man die Sehne CH parallel mit FG und verbinde H mit A. Trifft nun CH den Durchmesser DB in K, so ist nach I. 46 und 47 HK = CK, und also AH parallel mit KE, was nach I. 22 unmöglich ist.
Lehrsatz 5. Wenn ein Durchmesser einer Ellipse oder eines Kreises eine nicht durch den Mittelpunkt gehende Sehne halbirt, so ist diese halbirte Sehne parallel der Tangente in einem Endpunkte dieses Durchmessers.

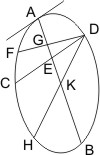
Sei eine Ellipse oder ein Kreisumfang mit dem Durchmesser AB gegeben, und werde eine nicht durch den Mittelpunkt gehende Sehne CD vom Durchmesser AB in E halbirt, so wird behauptet, dass CD parallel der im Endpunkt A des Durchmessers gezogenen Tangente ist. Wäre dies nicht der Fall, so sei DF parallel mit der Tangente; wird nun DF vom Durchmesser in G getroffen, so ist DG = GF und CF parallel mit GE, was unmöglich ist. Denn entweder ist G der Mittelpunkt des Kegelschnitts, dann muss nach I. 23 die verlängerte CF mit dem Durchmesser zusammentreffen, oder G ist nicht der Mittelpunkt, dann ziehe man von D durch den Mittelpunkt K die Sehne DKH, dann ist also DK = KH und also CH parallel mit AB; es war aber auch CF parallel AB, also lägen die drei Punkte C, F, H in gerader Linie, was unmöglich ist; also ist die Linie DC parallel der Tangente in A.
Lehrsatz 6. Wenn mit einer Tangente eines Kegelschnitts oder Kreises eine parallele Sehne gezogen und der Berührungspunkt der Tangente mit dem Mittelpunkt der Sehne verbunden wird, so ist diese Verbindungslinie ein Durchmesser.

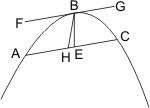
Sei ein Kegelschnitt oder ein Kreis ABC mit der Tangente FG in B gegeben, parallel mit FG die Sehne AC gezogen, und ihre Mitte E mit dem Berührungspunkt B verbunden, so wird behauptet, dass BE ein Durchmesser ist. Wäre dies nicht der Fall, so sei BH ein Durchmesser, dann müsste AH = HG sein, was unmöglich ist, da AE = EC nach Voraussetzung. Also ist BH kein Durchmesser, und ebenso wenig eine andere Linie ausser BE.
Lehrsatz 7. Wenn eine gerade Linie eine Hyperbel in zwei Punkten schneidet, so trifft sie an beiden Seiten verlängert mit den Asymptoten zusammen und die beiden Abschnitte derselben, die zwischen den Asymptoten und der Hyperbel liegen, sind gleich.

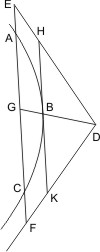
Sei eine Hyperbel ABC mit den Asymptoten DE, DF gegeben, und werde dieselbe von der Geraden AC in den Punkten A und C getroffen, so wird behauptet, dass AC mit beiden Asymptoten zusammentrifft. Sei G die Mitte von AC, so ist DG ein Durchmesser der Hyperbel, weshalb die Tangente im Scheitel B desselben parallel mit AC ist. Diese Tangente trifft nach § 3 mit den Asymptoten zusammen, also muss auch ihre Parallele AC mit denselben Linien zusammentreffen. Seien nun H, K die Punkte, in denen die Tangente, E, F die Punkte, in denen AC die Asymptoten trifft, so ist, weil HB = KB, auch EG = FG, und da AG = CG, auch EA = CF, was zu beweisen war.
Lehrsatz 8. Wenn eine gerade Linie, die die Asymptoten trifft, von der Hyperbel halbirt wird, so hat sie nur einen Punkt mit dieser gemein.

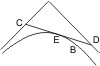
Trifft eine Gerade die Asymptoten in den Punkten C und D, und die Hyperbel in E, so dass CE = DE ist, so kann sie die Hyperbel nicht in einem zweiten Punkt in B treffen, denn sonst müsste nach vorigem Satz CE = BD sein, was unmöglich ist.
Lehrsatz 9. Wenn eine gerade Linie eine Hyperbel und ihre Asymptoten schneidet, so ist das Rechteck aus den Abschnitten, die auf ihr zwischen einem Hyperbelpunkt und den beiden Asymptote liegen, gleich dem vierten Theil des Rechtecks, das zu dem die Gerade halbirenden Durchmesser gehört.

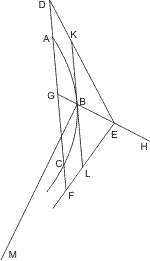
Sei eine Hyperbel ABC mit den Asymptoten ED, EF und einer Geraden, die die Hyperbel in A, C, die Asymptoten in D, F schneidet, gegeben. Man ziehe vom Mittelpunkt E nach der Mitte G von AC eine Linie, die die Hyperbel in B trifft, verlängere EB um sich selbst bis H, errichte senkrecht auf HB in B das zum Latus transversum RB gehörige Latus rectum BM, so wird behauptet: AD · AF = ¼ · HB · BM.
Man ziehe noch in B die Tangente, die die Asymptoten ED, EF in K und L schneidet. Nun ist:
1. DG² : EG² = BK² : EB² = ¼ HB · BM : EB²
2. AG² : EG² - EB² = BM : HB = ¼ · HB · BM : EB², also
3. DG² : EG² = AG² : EG² - EB², oder
4. DG² - AG² : EB² = DG² : EG² = ¼ · HB · BM : EB³, also
DG² - AG² = ¼ HB · BM. Da aber DG² - AG² = AD · AF, ist AD · AF = ¼ · HB · BM. q. e. d.
Lehrsatz 10. Wenn eine gerade Linie beide Schenkel des Nebenwinkels vom Asymptotenwinkel durchschneidet, so trifft sie die Hyperbel nur in einem Punkt und das Rechteck aus den Abschnitten, die auf ihr zwischen dem Hyperbelpunkt und den Asymptoten liegen, ist gleich dem Quadrat der Hälfte des mit dieser Geraden parallelen Durchmessers.

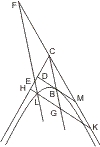
Sei eine Hyperbel zwischen den Asymptoten CH, CK gegeben und werde der Nebenwinkel von KCH von einer Geraden in den Punkten E, F getroffen, so wird zuerst behauptet, dass die Linie EF die Hyperbel nur in einem Punkte schneide. Man ziehe von C eine Parallele mit EF, so muss diese in den Asymptotenwinkel selbst hinein fallen und die Hyperbel in einem Punkte B treffen nach § 2, und also ein Durchmesser sein; folglich kann nach I 26 EF nur in einem Punkte die Hyperbel schneiden. Sei L der Schneidungspunkt, so wird behauptet: LF · LE = CB².
Man ziehe in B die Tangente, die die Asymptoten CH, CK in den Punkten D, M schneidet, und von L parallel damit die Ordinate LG, die die Asymptoten in den Punkten H und K trifft. Nun ist:
1. LH : HG = LE : GC,
2. LK : GK = LF : GC, also
3. LH · LK : HG² = LF · LE : GC², oder da
  HG² : GC² = DB² : BC²,
4. LH · LK : DB² = LF · LE : CB²,
und da nach vorigem Satz LH · LK = DB², ist auch:
- LF · LE = CB². q. e. d.
Lehrsatz 11. Wenn von einem Punkte einer Hyperbel bis an jede der beiden Asymptoten eine gerade Linie und von einem andern Punkte derselben Parallelen mit den gezogenen Linien bis an dieselben Asymptoten gezogen werden, so ist das Rechteck aus den vom ersten Punkt gezogenen Linien gleich dem Rechteck aus den vom andern Punkt gezogenen.

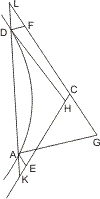
Sei eine Hyperbel ABD mit den Asymptoten CE, CF gegeben, und von einem Punkt A derselben an die Asymptoten die Linien AE, AG, von einem andern Punkt D die Linien DH, DF parallel je einer der vorigen bis an die entsprechenden Asymptoten gezogen, so wird behauptet:
- AE · AG = DF · DH.
Man ziehe noch AD, welche die Asymptoten in K, L trifft, so ist
1. AE : AG = AK : DK,
2. AG : DF = AL : DL, also
3. AG · AE : DF · DH = AK · AL : DK · DL, und da
AK · AL = DK · DL nach § 8, so ist auch
- AG · AE = DF · DH.
Lehrsatz 12. Wenn in dem Raum zwischen der Hyperbel und den Asymptoten eine Parallele mit der einen Asymptote gezogen wird, so trifft sie mit der Hyperbel und zwar nur in einem Punkte zusammen.

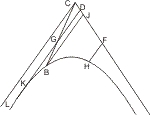
Sei eine Hyperbel LBH mit den Asymptoten CE, CF gegeben und in dem Raum zwischen ihnen die Linie DG parallel mit CE gezogen, so wird behauptet, dass dieselbe mit der Hyperbel und zwar nur in einem Punkte zusammentrifft.
Träfe sie nicht mit derselben zusammen, so sei H ein beliebigen Punkt der Hyperbel und von ihm HF parallel mit EC bis an die Asymptote gezogen, werde ferner auf DG der Punkt G so bestimmt, dass CD · DG = CF · FH ist, dann CG gezogen, bis es die Hyperbel in B trifft (siehe § 2), und endlich von B an die Asymptote CF die Linie BJ parallel EC gezogen, so müsste BJ · CJ = HF · CF = CD · DG sein, was unmöglich ist, da CD : CJ = DG : BJ ist. Träfe aber die Linie DG die Hyperbel in zwei Punkten K und L, so müsste CD · DK = CD · DL sein, was ebenfalls unmöglich ist.
Also trifft die Linie DG die Hyperbel nur in einem Punkt.
Lehrsatz 13. Wenn eine Hyperbel und ihre Asymptoten ins Unendliche verlängert werden, so kommen sie einander immer näher, so dass ihre wechselseitige Entfernung kleiner wird als irgend eine angebbare Grösse.

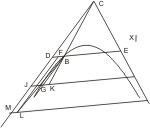
Sei eine Hyperbel mit den Asymptoten CD, CE gegeben, so wird zuerst behauptet, dass sich die Hyperbel den Asymptoten nähert, je weiter beide verlängert werden.
Seien DE, JH zwei parallele, zwischen den Asymptoten gezogene Linien, DE aber, die dem Mittelpunkt näher liegt, begegne der Hyperbel in B; zieht man CB, bis es JH in K trifft, so ist K innerhalb der Hyperbel. Sei nun G der Schneidungspunkt der Hyperbel mit JK, so ist, weil DB · BE = JG · GH und GH > BE, auch nothwendig DB > JG; also nähert sich die Hyperbel, je weiter sie verlängert wird, desto mehr der Asymptote CD. Sei nun X eine gegebene kleine Länge, so schneide man auf DB ein Stück DF < X ab und ziehe von F eine Parallele mit CD, so muss diese nach § 13 die Hyperbel in einem Punkt L treffen; zieht man nun noch durch L eine Parallele mit DE, die die verlängerte CD in M trifft, so ist LM = DF und mithin kleiner als X; also wird die Entfernung zwischen der Asymptote und der Hyperbel zuletzt kleiner als irgend eine angehbare Grösse.
Anm. des Uebersetz. Die kürzeste Entfernung von einem Hyperbelpunkt zur Asymptote ist das Loth; wenn also LM nicht senkrecht auf CM ist, so wird die eigentliche Entfernung noch kürzer als LM sein.
Anm. Aus dem Gesagten ist klar, dass die Linien CD, CE der Hyperbel näher kommen, als irgend andere gerade Linien, die nicht die Hyperbel selbst treffen, und dass es keinen kleineren Winkel als DCE giebt, zwischen dessen Schenkeln sich die Hyperbel befindet.
Zu dieser Anmerkung haben sich in den verschiedenen Exemplaren, die Eutocius benutzt hat, noch längere Auseinandersetzungen gefunden, welche Eutocius selbst weggelassen hat, weil sie ihm überflüssig erschienen und von denen er nur einen kurzen Bericht giebt; man kann sich den Inhalt derselben leicht vergegenwärtigen, wenn man alle Fälle zeichnet, in denen ein Winkel eine Hyperbel zwischen seinen Schenkeln enthält, und jedesmal zeigt, dass dieser Winkel nicht kleiner sein kann, als der Asymptotenwinkel. Auch ein Lemma des Pappus, worin bewiesen wird, dass zwei zu denselben Asymptoten gehörige Hyperbeln sich nicht schneiden, einander aber näher kommen als irgend angebbar ist, findet sich von Commandinus an diese Stelle gesetzt; die Richtigkeit des ersten Theils dieser Behauptung ergiebt sich fast unmittelbar aus § 8, und der zweite Theil folgt eben so leicht aus § 14.
Lehrsatz 14. Gegenschnitte haben dieselben Asymptoten.
Da die Tangenten an den Gegenschnitten, welche in den Endpunkten eines Durchmessers gezogen werden, parallel sind, und die Stücke, welche auf jeder derselben vom Scheitelpunkt aus nach § 1 abgeschnitten werden müssen, um die Asymptoten zu erhalten, gleich sind, so erhellt leicht, dass jede Asymptote des einen Gegenschnitts die Verlängerung einer Asymptote des andern ist.
Lehrsatz 15. Wenn beide Schenkel des Nebenwinkels eines Asymptotenwinkels, in dem und dessen Scheitelwinkel sich Gegenschnitte befinden, von einer geraden Linie geschnitten werden, so trifft diese auch jeden der Gegenschnitte in einem Punkt und die Abschnitte derselben zwischen den Asymptoten und den Hyperbeln sind einander gleich.

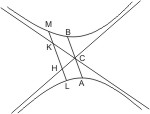
Seien zwei Gegenschnitte mit den Scheiteln A, B dem Mittelpunkt C und den Asymptoten DCG, ECF gegeben und eine gerade Linie gezogen, die DC in H, CF in K schneidet, so wird behauptet, dass dieselbe mit jedem der Gegenschnitte nur in einem Punkt zusammentreffe. Dies folgt aus § 11 für jede der beiden Hyperbeln einzeln. Seien nun L und M die Punkte, in denen die Gegenschnitte getroffen werden, und werde durch C ein Durchmesser AB parallel LM gezogen, so ist ebenfalls nach § 11, HL · LK = AC², HM · MK = B², also BL · LK = HM · MK und deshalb auch HL = MK.
Lehrsatz 16. Conjugirte Gegenschnitte haben dieselben Asymptoten.

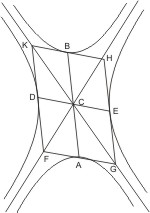
Seien zwei Paar conjugirte Gegenschnitte mit den conjugirten Durchmessern AB, DE und dem Mittelpunkt C gegeben, so wird behauptet, dass sie gemeinsame Asymptoten haben.
Man ziehe in den Punkten A, B,D, E die Tangenten an die Hyperbeln, welche FAG, GEH, HBK, KDF heissen. Nun sind FG und KH parallel DE, und FK und GH parallel AB, (I. 56); also FKHG ein Parallelogramm und die Diagonalen desselben GK, FH geben durch den Punkt C und halbiren sich daselbst. Da nun DE² gleich dem zum Durchmesser AB gehörigen Rechteck ist, ist DC² oder jedes der vier Quadrate KB², BH², AG², AF² gleich dem vierten Theil des zum Durchmesser AB gehörigen Rechtecks, mithin KG, FH die Asymptoten für die Gegenschnitte mit den Scheiteln A; und B, und auf ganz dieselbe Weise wird gezeigt, dass sie es auch für die Gegenschnitte mit den Scheiteln D und E sind.
Lehrsatz 17 und 18. Wenn an einem von zwei Paaren conjugirter Gegenschnitte eine Tangente gezogen wird, so trifft dieselbe jeden der daneben liegenden Gegenschnitte je in einem Punkt, und der Berührungspunkt ist die Mitte zwischen diesen beiden Schneidungspunkten.

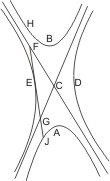
Seien conjugirte Gegenschnitte A, B, D, E gegeben und im Punkte E an einen derselben eine Tangente gezogen, so wird zuerst behauptet, dass diese Tangente die beiden daneben befindlichen Gegenschnitte je in einem Punkte trifft. Seien CF, CG die Asymptoten der Schnitte, so muss die Tangente nach § 3 dieselben treffen, und deshalb nach § 11 auch die daneben befindlichen Gegenschnitte.
Seien nun I, H die Schneidungspunkte, so wird ferner behauptet, dass EI = EH ist. Sind G und F die Punkte, in denen die Asymptoten geschnitten werden, so ist nach § 2 GE = EF und nach § 16 IG = FH, also auch EI = EH. q. e. d.
Lehrsatz 19. Wenn an einen von zwei Paaren conjugirter Gegenschnitte eine Tangente, und vom Mittelpunkt eine Linie nach dem Berührungspunkt und eine andere parallel mit der Tangente bis zum Durchschnitt mit den conjugirten Schnitten gezogen werden, so ist die Tangente in einem dieser zuletzt erwähnten Schneidungspunkte parallel der Linie vom Mittelpunkt nach dem Berührungspuukt der ersten Tangente, und die Linien, welche durch den Mittelpunkt nach den Berührungspunkten gehen, sind conjugirte Durchmesser der Gegenschnitte.

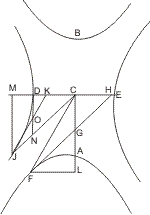
Seien zwei Paar conjugirte Gegenschnitte A, B, D, E und an einem Punkt F eines derselben eine Tangente FGH gegeben, vom Mittelpunkt. C aber eine Linie nach F und eine Parallele mit FGH gezogen, welche den conjugirten Schnitt D in I trifft, so wird behauptet:
1. dass die in I gezogene Tangente IK ‖ CF ist,
2. dass die verdoppelten FC, IC conjugirte Durchmesser sind.
Beweis. Man ziehe von F an den Durchmesser CA die Ordinate FL und von I an den zu CA conjugirten Durchmesser CD die Ordinate IM. Nun ist, wenn r das zu BA gehörige latus rectum bedeutet:
1. FL² : LG · LC = r : AB nach I § 37,
2. MI² : MK · MC = AB : r nach I. § 56 und § 37 also
- FL² : LG · LC = MK · MC : MI², da aber
- FL : LG = MC : MI wegen Aehnlichkeit der Dreiecke FLG, CMI, muss auch
- FL : LC = MK : MI und also auch
- ∆FLC ∾ ∆KMI;
nun ist ∠ICL = ∠MIC und subtrahirt man davon ∠FCL = ∠MIK, so bleibt ∠FCI = ∠KIC, also FC ‖ KI.
Bedeutet ferner S das Latus rectum für das latus transversum 2 · CI, so ist zweitens zu zeigen, dass
- CI : CF = CF : ½ · S.
Man ziehe noch im Scheitel D eine Tangente, die IK in 0, IC in N trifft, so ist
1. IN : IO = 2 · IK : S (I. 50), oder da
  IN : IO = FG : FC
2. FG : CF = IK : ½ · S. Es ist aber
  CH : CD = CD : FL, mithin
3. CH : FL = HG : FG = CH² : CD², oder
4. ∆CHG : ∆FGC = ∆CHG : ∆DNC, also
- ∆FGC = ∆DNC = ∆IKC (2. Bew, von I. 43).
Da nun ∠KIC = ∠GFC, muss FG : IK = CI : CF, welches oben in (2) substituirt giebt CI : CF = CF : ½ · S. Auf dieselbe Weise kann gezeigt werden, dass CI zu CF wie CF zu dem zu 2 · CF gehörigen Latus rectum sich verhält. Mithin sind 2 · IC, 2 · FC conjugirte Durchmesser.
Lehrsatz 20. Unter denselben Voraussetzungen ist zu zeigen, dass der Punkt, in welchem die Tangenten in den Endpunkten zweier conjugirter Durchmesser zusammentreffen, auf einer Asymptote liegt.

Seien conjugirte Gegenschnitte mit den conjugirten Durchmessern AB, DE und dem Centrum C gegeben, und F der Schneidungspunkt der in A und D gezogenen Tangenten, so wird behauptet, dass F auf einer Asymptote liegt.
CD² ist gleich dem vierten Theil des zum Durchmesser AB gehörigen Rechtecks, und da AF = CD ist, ist nach § 1 CF eine Asymptote, mithin F ein Punkt auf derselben.
Lehrsatz 21. Wenn in conjugirten Gegenschnitten vom Mittelpunkt an einen der Schnitte eine Linie und eine zweite parallel der ersten so gezogen wird, dass sie einen der benachbarten Schnitte durchschneidet und bis an die Asymptoten reicht, so ist das Rechteck aus den Abschnitten dieser Linie zwischen einem Punkt der Hyperbel und den beiden auf den Asymptoten gleich dem Quadrat der zuerst vom Mittelpunkt an einen Schnitt gezogenen Linie.

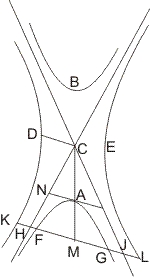
Seien conjugirte Gegenschnitte A, B, D, E mit dem Mittelpunkt C gegeben, und von C an einen derselben die Linie CD, parallel mit CD aber eine andere Linie gezogen, die den benachbarten Schnitt A in den Punkten F und G, die Asymptoten in den Punkten H und I trifft, so ist zu zeigen, dass
- HF · FI = CD²
Ist M die Mitte von FG, so ist CM der zu der Ordinate FM gehörige Durchmesser, und wenn A der Punkt ist, in welchem CM die Hyperbel trifft, die Tangente in A parallel mit FM und CD. Ist nun AN das Stück derselben bis zu einer Asymptote, so ist AN² = HF · FI nach § 10, aber da nach § 20 CA und CD conjugirte Durchmesser sind, ist AN = CD, also auch CD² = HF · FJ.
Lehrsatz 22. Wenn in conjugirten Gegenschnitten vom Mittelpunkt aus an einen der Schnitte eine Linie und parallel damit eine andere gezogen wird, welche drei benachbarte Schnitte trifft, so ist das Rechteck aus den Abschnitten dieser Linie, die zwischen einem Punkt des mittleren Schnitts und den beiden auf den benachbarten Schnitten liegen, gleich dem doppelten Quadrat der zuerst gezogenen Linie.
Seien conjugirte Gegenschnitte A, B, D, E gegeben, und vom Mittelpunkt C an einen derselben eine Linie CD, parallel damit aber eine andere Linie gezogen, die den Schnitt A in den Punkten F, G, die benachbarten Schnitte D und E aber in den Punkten K und L trifft, so wird behauptet, dass KF · FL = 2 · CD².
Man ziehe noch die Asymptoten, welche die Linie FG in den Punkten H und I treffen, und nenne M die Mitte zwischen F und G, so ist also auch M die Mitte zwischen K und L und zwischen H und I.
Nun ist
1. CD² = HF · FI = MH² - MF² nach § 22,
2. CD² = HK · KI = MK² - MH² nach §11. Also
3. 2 · CD² = MK² - MF² = KF · FL. q. e. d.
Lehrsatz 23. Wenn zwei Linien eine Parabel jede in zwei Punkten so schneiden, dass kein Durchschnittspunkt der einen zwischen den Durchschnittspunkten der andern liegt, so schneiden sich die beiden Linien ausserhalb der Parabel.

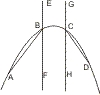
Sei eine Parabel ABCD gegeben, welcher zwei, Gerade AB und CD so begegnen, dass keiner der Durchschnittspunkte A und B der einen zwischen den Durchschnittspunkten C und D der andern liegt, so wird behauptet, dass AB, CD ausserhalb der Parabel zusammentreffen. Man ziehe durch B und C die Durchmesser EBF, GCH, so sind diese parallel und treffen jeder die Parabel nur in einem Punkt; verbindet man also BC, so sind die Winkel FBC, HCB zusammen gleich zwei Rechten; also bilden AB, DC in ihren Verlängerungen mit BC Winkel, die zusammen kleiner als zwei Rechte sind, und folglich, treffen sich diese Verlängerungen ausserhalb des Schnitts.
Lehrsatz 24. Wenn zwei Linien eine Hyperbel jede in zwei Punkten so schneiden, dass kein Durchschnittspunkt der einen zwischen den Durchschnittspunkten der andern liegt, so schneiden sich die beiden Linien ausserhalb der Hyperbel, jedoch innerhalb des Asymptotenwinkels.

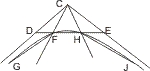
Sei eine Hyperbel mit den Asymptoten CD, CE gegeben und von zwei geraden Linien FG, HI so durchschnitten, dass nicht einer der Punkte H, I zwischen den Punkten F, G liegt, so wird behauptet, dass die Linien GF, IH ausserhalb der Hyperbel, jedoch innerhalb des Winkelraums DCE zusammentreffen. Man ziehe CF, CH und verbinde F mit H. Weil nun die Verlängerungen der Geraden GF, IH innerhalb der Winkel CFH, CHF fallen, diese Winkel zusammengenommen kleiner als zwei Rechte sind, so müssen sie innerhalb des Dreiecks CFH, also auch innerhalb des Winkelraums DCE zusammen kommen.
Anm. Auf gleiche Weile kann dasselbe von zwei die Hyperbel berührenden Geraden gezeigt werden.
Lehrsatz 25. Wenn in einer Ellipse oder einem. Kreise zwei Sehnen, die nicht durch den Mittelpunkt geben, sich schneiden, so werden sie sich nicht gegenseitig halbiren.

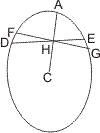
Wäre es möglich, dass in einer Ellipse oder einem Kreis zwei Sehnen DE, FG sich gegenseitig halbirten, ohne durch den Mittelpunkt C zu gehen, so ziehe man von C nach ihrem Schneidungspunkt H bis an den Umfang in .A eine Linie, dann ist CA ein Durchmesser, welcher DE halbirt, also die Tangente in .A. parallel mit DE; auf gleiche Weise müsste sie aber auch parallel mit FG sein, was unmöglich ist, also können DE, FG sich nicht gegenseitig halbiren.
Lehrsatz 26. Wenn die Verbindungslinie der Berührungspunkte zweier Tangenten einer Ellipse oder eines Kreises durch den Mittelpunkt dieses Schnitts geht, so sind die Tangenten parallel; wenn die Berührungssehne aber nicht durch den Mittelpunkt geht, so treffen die Tangenten auf der dem Mittelpunkte abgewandten Seite derselben zusammen.

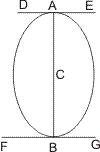
Sei eine Ellipse oder ein Kreis mit dem Mittelpunkt C und zwei Tangenten in A und B gegeben, und gehe die Linie AB durch den Mittelpunkt C, so wird behauptet, dass die Tangenten parallel sind. Die Tangente DE ist nach § 6 parallel den zum Durchmesser AB gehörigen Ordinaten, deren es nach § 26 nicht zwei verschiedene in demselben Punkt geben kann; und da ein Gleiches auch von der Tangente FG im Punkte B gilt, so ist bewiesen, dass DE parallel FG ist.

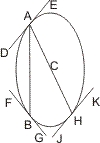
Geht aber AB nicht durch den Mittelpunkt, so ziehe man von A den Durchmesser AH; dann ist die Tangente in H parallel mit DE, also muss die Tangente in B mit DE zusammentreffen und zwar in dem Theile AD und seiner Verlängerung, also auf der dem Mittelpunkt abgewandten Seite von AB; denn da die Ellipse selbst ohne Unterbrechung von A bis H fortläuft, die Tangente in B aber ganz ausserhalb derselben liegt ist es offenbar unmöglich, dass sie mit den in A und H gezogenen Tangenten parallel sein kann, in welchem Fall sie ja die innerhalb der Ellipse liegende Gerade AH schneiden müsste.
Lehrsatz 27. Wenn in einem Kegelschnitt oder einem Kreise eine Linie zwei parallele Sehnen halbirt, so ist sie ein Durchmesser des Schnitts.

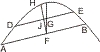
Sei ein Kegelschnitt mit den beiden parallelen Sehnen AB, DE gegeben, und deren Mitten F und G verbunden, so wird behauptet, dass FG ein Durchmesser ist. Wäre dies nicht der Fall, so sei FH der von F gezogene Durchmesser, der DE in J trifft. Nun müsste auch DJ = JE sein, was unmöglich ist; also kann keine andere Linie ein Durchmesser sein als FG.
Anm. des Eutocius. Dieser Satz bietet in Verbindung mit den früheren ein leichtes Mittel zu untersuchen, ob eine vorgelegte Curve ein Kegelschnitt ist und zu welcher der vier Arten derselben er gehört. Man ziehe von 2 Punkten der vorgelegten Curve 2 Paar paralleler Sehnen und verbinde die Mitten jedes Paars. Halbirt nun jede dieser Verbindungslinien alle der entsprechenden Richtung parallelen Sehnen, so ist die vorgelegte Curve ein Kegelschnitt. Sind die beiden Verbindungslinien parallel, so ist sie eine Parabel, divergiren sie nach dem Innem der Curve zu, so ist sie eine Hyperbel, im andem Falle ein Kreis oder eine Ellipse, je nachdem die Halbmesser alle gleich oder nicht alle gleich sind.
Lehrsatz 28. Wenn zwei Tangenten eines Kegelschnitts oder eines Kreises sich in einem Punkt treffen, und von diesem Punkt nach der Mitte der Berührungssehne eine Linie gezogen wird, so ist dieselbe ein Durchmesser des Kegelschnitts.

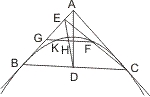
Sei ein Kegelschnitt BLC und in B und C die Tangenten, die sich in A treffen, gegeben; wird nun von der Mitte D von BC eine Linie nach A gezogen, so ist zu beweisen, dass diese Linie ein Durchmesser ist. Wäre sie es nicht, so ziehe man von D aus den Durchmesser, dann wird derselbe eine der Tangenten vor dem Punkte A treffen müssen; treffe er also BA in E. Zieht man nun CE, so muss diese Linie den Kegelschnitt noch in einem Punkt treffen (I, 36); ist also F dieser Punkt, so ziehe man durch F parallel mit BC eine Linie, welche den Kegelschnitt zum zweiten Mal in K, die Tangente BA in G, und den Durchmesser DE in H trifft; weil nun BD = CD, muss auch GH = HF, und da der Durchmesser ED die Sehne BC halbirt, muss er auch die parallele Sehne KF halbiren, was unmöglich ist; also kann nicht eine andere Linie als DA der durch D gebende Durchmesser sein.
Lehrsatz 29. Wenn zwei Tangenten eines Kegelschnitts oder eines Kreises in einem Punkt sich treffen, so halbirt der von diesem Punkt aus gezogene Durchmesser die Berührungssehne.

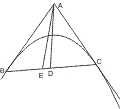
Sei ein Kegelschnitt BC mit den Tangenten in B und C, die sich in A treffen, gegeben; wird nun von A aus ein Durchmesser gezogen, so ist zu beweisen, dass derselbe die Berührungssehne BC in D halbirt. Wäre dies nicht der Fall, so sei E die Mitte von BC; dann müsste nach vorigem Satz EA ebenfalls ein Durchmesser sein, was unmöglich ist. Denn ist der Kegelschnitt eine Ellipse oder ein Kreis, so müsste der Mittelpunkt A ausserhalb liegen, ist er eine Parabel, so müssten sich zwei Durchmesser schneiden, und ist er endlich eine Hyperbel, so müssten sich zwei Tangenten derselben im Scheitelpunkt des Asymptotenwinkels schneiden, was nach § 25 Anm. ebenfalls unmöglich ist. Also ist kein anderer Punkt ausser D die Mitte von BC.
Lehrsatz 30. Wenn zwei Gegenschnitte und an jedem eine Tangente gegeben sind und die Verbindungslinie der Berührungspunkte durch den Mittelpunkt geht, so sind die Tangenten parallel, geht sie aber nicht durch den Mittelpunkt, so schneiden sich die Tangenten und zwar auf derselben Seite, auf welcher der Mittelpunkt liegt.

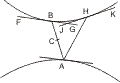
Seien zwei Gegenschnitte mit den Tangenten in A und B gegeben, und gehe erstens die Verbindungslinie AB durch den Mittelpunkt C, so wird behauptet, dass die Tangenten DE und FG parallel sind. Nach I. 48 halbirt ACB die im Schnitt B parallel mit DE gezogenen Sehnen, also ist die im Scheitel B parallel mit DE gezogene Linie eine Tangente nach I. 32, und da es nicht zwei verschiedene Tangenten in B giebt, ist die daselbst gezogene Tangente FG auch parallel mit DE. Geht nun zweitens die Verbindungslinie der Berührungspunkte A, H zweier Tangenten DE und JK nicht durch den Mittelpunkt, so ziehe man von A durch C die Linie AB, und in B die Tangente FG; nun müssen sich die Tangenten in B und H innerhalb des Asymptotenwinkels schneiden, folglich schneidet HK auch die mit FG parallele Linie DE und zwar auf derselben Seite von AH, auf welcher der Mittelpunkt liegt.
Lehrsatz 31. Wenn zwei Gegenschnitte gegeben sind, und jeder von einer Geraden in zwei Punkten geschnitten oder auch in einem Punkt berührt wird, diese beide Geraden aber nicht parallel sind, so muss ihr Schneidungspunkt in einem der beiden Nebenwinkel des Asymptotenwinkels liegen.

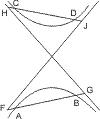
Seien zwei Gegenschnitte von zwei Geraden AB, DC je in zwei Punkten geschnitten, und FJ, GH die Asymptoten, dann wird behauptet, dass AB, CD, wenn sie nicht parallel sind, sich in einem der Nebenwinkel FCH, GCJ des Asymptotenwinkels schneiden.
Nach § 8 muss AB sowohl als CD beide Asymptoten schneiden, also können sie nur in dem Raum der Nebenwinkel mit einander zusammentreffen. Ein Gleiches gilt auch, wenn eine oder beide Linien die Hyperbeln nur berühren.
Lehrsatz 32. Wenn einer von zwei Gegenschnitten von einer Geraden entweder in zwei Punkten geschnitten oder berührt wird, so trifft diese Gerade nicht den andern Gegenschnitt, sondern geht durch drei Winkelräume, nämlich den zu dem betreffenden Schnitt gehörigen Asymptotenwinkel und seine beiden Nebenwinkel.

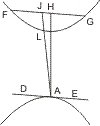
Seien zwei Gegenschnitte gegeben, und einer derselben von einer Geraden in zwei Punkten A, B geschnitten, so wird behauptet erstens, dass AB nicht den andern Gegenschnitt trifft. Man ziehe die Asymptoten; dann schneidet AB beide Asymptoten in F und G, und da sie dieselben nicht zum zweiten Male schneiden kann, wird sie nicht in den Scheitelwinkel des Asymptotenwinkels gelangen können, also erstens den zweiten Gegenschnitt nicht treffen, und zweitens durch die drei Winkelräume gehen.
Lehrsatz 33. Wenn an einem von zwei Gegenschnitten eine Tangente und in dem andern eine damit parallele Sehne gezogen sind, so ist die Linie vom Berührungspunkt der Tangente nach der Mitte der Sehne ein Durchmesser.
Seien zwei Gegenschnitte A,B und an einem derselben in A eine Tangente DE, im andern eine mit DE parallele Sehne FG gegeben; ist nun H die Mitte von FG, so soll bewiesen werden, dass AH ein Durchmesser ist. Wäre dies nicht der Fall, so ziehe man von A den Durchmesser, der den Gegenschnitt in L, die Sehne FG in J trifft. Da nun nach § 31 die Tangente in L parallel DE ist, muss sie auch parallel FG und folglich J die Mitte von FG sein, was unmöglich ist; also kann keine andere Linie als AH der von A. ausgehende Durchmesser sein.
Lehrsatz 34. Wenn ein Durchmesser eine Sehne in einem von zwei Gegenschnitten halbirt, so ist die Tangente im Endpunkt des Durchmessers an den andern Gegenschnitt gezogen der Sehne parallel.
Nach I. 32 ist die Tangente, die im Endpunkt des Durchmessers an denselben Gegenschnitt, in dem die Sehne liegt, gezogen wird, parallel der Sehne, und da sie nach § 31 auch parallel der Tangente ist, die im Endpunkt des Durchmessers an den andern Gegenschnitt gezogen wird, ist diese letztere gleichfalls der Sehne parallel.
Lehrsatz 35. Wenn in zwei Gegenschnitten parallele Sehnen gezogen werden, so ist die Verbindungslinie ihrer Mitten ein Durchmesser der Gegenschnitte.

Seien A und B zwei Gegenschnitte, DE, FG zwei parallele Sehnen je in einem derselben, und H, J die Mitten dieser Sehnen so wird behauptet, dass HJ ein Durchmesser ist. Wäre er es nicht, so sei von H der Durchmesser gezogen, der die Schnitte in A,B, FG in K trifft; nun muss die Tangente in A parallel mit DE, also auch parallel mit FG sein, also FK = KG, was unmöglich ist. Also ist keine andere Linie ausser HJ der von H ausgehende Durchmesser.
Lehrsatz 36. Wenn eine nicht durch den Mittelpunkt gezogene Linie zwei Gegenschnitte durchschneidet, so sind die vom Mittelpunkt nach der Mitte dieser durchschneidenden Geraden und parallel mit derselben gezogenen Linien zwei conjugirte Durchmesser der Gegenschnitte.

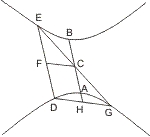
Seien zwei Gegenschnitte A und B von einer nicht durch den Mittelpunkt gehenden Geraden in den Punkten D und E geschnitten, vom Mittelpunkt C aber eine Linie parallel DE, die die Schnitte in A und B trifft, und eine andere nach der Mitte F von DE gezogen, so wi'rd behauptet; dass diese Linien CA,CF conjugirte Durchmesser sind.
Man ziehe EC, und verlängere es, bis es den Gegenschnitt in G schneidet, ziehe DG und verlängere CA, bis es DG in H trifft. Nun ist EC = CG und weil auch EF = DF, die Linie DG parallel FC. Da ferner CA parallel DE, muss DH = HG, also auch die Tangente in A parallel mit DG oder CF sein, folglich sind CA, CF conjugirte Durchmesser (I. 16).
Lehrsatz 37. Wenn an jeden von zwei Gegenschnitten eine Tangente gezogen wird und diese Tangenten nicht parallel sind, dann ist die Linie von ihrem Schneidungspunkt nach der Mitte der Berührungssehne ein zweiter Durchmesser der Gegenschnitte und der zugehörige erste Durchmesser eine Parallele mit der Berührungssehne durch den Mittelpunkt.

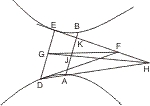
Seien zwei Gegenschnitte A und B gegeben, und an einen derselben in D, an den andern in E Tangenten gezogen, die sich in F treffen; ist nun G die Mitte von DE, so ist zu beweisen, dass FG ein zweiter Durchmesser der Gegenschnitte ist. Wäre das nicht der Fall, so ziehe man von G einen solchen Durchmesser, der die über F verlängerte Tangente EF in H trifft, so muss die gerade Linie DH den Gegenschnitt A noch in einem Punkt treffen (I. 36); ist nun A dieser Punkt, so ziehe man durch A eine Parallele mit DE, welche GH in J, EH in K und den andern Gegenschnitt in B trifft. Nun müsste, weil GH ein Durchmesser und DG = GE, AB aber parallel DE ist, auch AJ = JB, und zugleich aus dem Dreieck DEH AJ = JK sein, was unmöglich ist; also ist keine andere Linie von G aus ein zweiter Durchmesser ausser GF. q. e. d.
Lehrsatz 38. Wenn an jeden von zwei Gegenschnitten eine Tangente gezogen wird und diese Tangenten sich in einem Punkt treffen, dann halbirt der von diesem Punkt aus gezogene Durchmesser die Verbindungslinie der Berührungspunkte.
Der Beweis wird ebenso wie der von § 30 geführt, und stützt sich zuletzt darauf, dass nicht zwei Tangenten an den Gegenschnitten im Mittelpunkt zusammentreffen können.
Lehrsatz 39. Wenn an jeden von zwei Gegenschnitten eine Tangente gezogen wird, diese Tangenten sich in einem Punkt treffen und durch ihren Schneidungspunkt eine Parallele mit der Berührungssehne bis an die Gegenschnitte gezogen wird, so sind die von den hierdurch auf den Gegenschnitten erhaltenen Punkten nach der Mitte der Bertürungssehne gezogenen Geraden Tangenten an den Gegenschnitten.

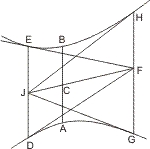
Seien zwei Gegenschnitte A und B gegeben und an A in D, an B in E Tangenten gezogen, die sich in F schneiden, sei ferner durch F eine Parallele mit DE gezogen, die den Gegenschnitten in G, H begegnet, und J die Mitte von DE, so wird behauptet, dass die Geraden GJ, HJ Tangenten an den Gegenschnitten sind.
Nach § 38 ist JF ein zweiter Durchmesser der Gegenschnitte; sei also der Punkt C derselben der Mittelpunkt, und werde durch C eine Parallele mit DE gezogen, welche die Gegenschnitte in A und B trifft; weil nun CJ die Linie DE halbirt, sind AB, CJ conjugirte Durchmesser und also DJ eine an den zweiten Durchmesser gezogene Ordinate; also ist nach I. 38. das Rechteck CJ · CF gleich dem Quadrat des halben zweiten Durchmessers. Da nun aber HF gleichfalls eine an den zweiten Durchmesser gezogene Ordinate ist, so folgt hieraus umgekehrt, dass JH und auf ähnliche Art, dass auch JG eine Tangente ist.
Lehrsatz 40. Wenn zwei Gegenschnitte von zwei nicht durch den Mittelpunkt gehenden und sich schneidenden Geraden getroffen werden, so können diese Geraden sich nicht gegenseitig halbiren.

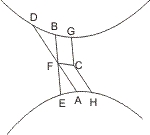
Seien zwei Gegenschnitte A und B von den nicht durch den Mittelpunkt C gehenden Geraden AD, EB, die sich in F schneiden, getroffen, so wird behauptet, dass diese Geraden sich nicht halbiren. Denn wäre dies der Fall, so ziehe man CF und durch C eine Parallele mit FA, welche den Gegenschnitt A in H, und eine andere Parallele mit FB, welche den Gegenschnitt B in G trifft; nun müsste, wie früher bewiesen, so wohl die Tangente in H, als die Tangente in G parallel CF sein, was unmöglich ist, da GH nicht durch den Mittelpunkt geht. Also können AD, EB sich nicht gegenseitig halbiren.
Lehrsatz 41. Wenn zwei Paar conjugirte Gegenschnitte von zwei nicht durch den Mittelpunkt gehenden Geraden getroffen werden, so können sich diese Geraden nicht halbiren.

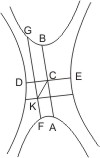
Seien conjugirte Gegenschnitte A und B, D und E gegeben und von zwei sich in K schneidenden Geraden FG, HJ, die nicht durch den Mittelpunkt C gehen, getroffen, so wird behauptet, dass diese Geraden sich nicht halbiren. Wäre dies der Fall, so ziehe man CK und durch C eine Parallele mit FG, welche die Gegenschnitte A und B in den Punkten A und B, und eine andere mit HJ, welche die Gegenschnitte D und E in den Punkten D und E trifft. Nun müssten, weil CK die der Geraden AB parallele Linie FG halbirt, CK und AB conjugirte Durchmesser, und also die Tangente in A parallel mit CK sein, und auf ähnliche Weise müssten CK, CD conjugirte Durchmesser, also die Tangente in D ebenfalls parallel CK sein; dies ist aber unmöglich, da nach § 19 die Tangente in A die beiden Gegenschnitte D und E und die Tangente in D die beiden Gegenschnitte A und B trifft, also die beiden Tangenten im Winkelraum DCA zusammentreffen müssen.
Lehrsatz 42. Wenn einen von zwei Paaren conjugirter Gegenschnitte eine gerade Linie in zwei Punkten schneidet und vom Mittelpunkt eine Linie nach der Mitte dieser Geraden und eine andere parallel damit gezogen werden, so sind diese Linien conjugirte Durchmesser der Gegenschnitte.

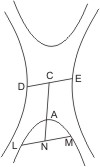
Seien A und B, D und E conjugirte Gegenschnitte und einer derselben A von einer Geraden in den Punkten L und M getroffen; wird dann vom Mittelpunkt C eine Linie nach der Mitte N von LM und eine andere DE parallel mit LM gezogen, so ist zu beweisen, dass diese beiden Linien conjugirte Durchmesser der Gegenschnitte sind. Nach § 5 ist die Tangente in A parallel mit LM, also auch mit der durch C damit gezogenen Parallelen DE, mithin sind nach § 20 CA, CD conjugirte Durchmesser der Gegenschnitte.
Aufgabe 2. In einem gegebenen Kegelschnitt einen Durchmesser zu finden.
Man ziehe z:wei parallele Sehnen und verbinde ihre Mitten. (Beweis durch Umkehrung von I. 46, 47 und 48.)
Aufgabe 3. In einer gegebenen Ellipse oder Hyperbel den Mittelpunkt zu finden.
Man suche nach § 44 zwei Durchmesser, so ist deren Schneidungspunkt der Mittelpunkt.
Aufgabe 4. In einer gegebenen Parabel die Achse zu finden.
Man suche nach § 44. einen Durchmesser, ziehe senkrecht dagegen eine Sehne, halbire dieselbe und ziehe durch ihre Mitte eine Parallele mit dem Durchmesser.
Aufgabe 5. In einer gegebenen Ellipse oder Hyperbel die Achsen zu finden.

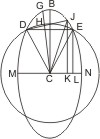
Man suche den Mittelpunkt C, nehme einen beliebigen Punkt D des Schnitts, beschreibe mit CD einen Kreis, der den Schnitt zum zweiten Mal in E trifft, und fälle von C auf DE ein Loth, so ist dies die eine Achse und die durch C mit DE gezogene Parallele MN die andere.
Lehrsatz 43. Nachdem die Achsen, wie in voriger Aufgabe gezeigt ist, gefunden sind, soll bewiesen werden, dass es keine andern Achsen giebt.
Sei, wenn es möglich ist, CG eine andere Achse, so fälle man von D auf CG das Loth DH, welches verlängert den Kegelschnitt zum zweiten Male in J trifft; dann ist DH = HJ, und, wenn man CJ zieht, auch CJ = CD, folglich auch CJ = CE; dies ist aber unmöglich. Denn zieht man noch von J und E senkrecht gegen MN die Ordinaten JK, EL, so müsste, weil CJ = CE, auch CK² + KJ² = CL² + LE² oder KJ² - LE² = CL² - CK² und wenn man CL² = CN² - ML · LN und CK² = CN² - MK · KN setzt, KJ² - LE² = MK · KN - ML · LN. Weil aber J und E Punkte des Kegelschnitts und IK, EL Ordinaten sind, ist KJ² : LE² = MK ·KN : ML · LN, also müsste KJ² = MK · KN sein. Dann aber wäre der Kegelschnitt MIN ein Kreis, was gegen die Voraussetzung ist.
Also können ausser den in § 47 construirten Achsen keine anderen gezogen werden.
Aufgabe 6. Wenn ein Kegelschnitt und ein nicht innerhalb befindlicher Punkt gegeben sind, durch den Punkt an den Kegelschnitt eine Tangente zu ziehen.
1. Ist der gegebene Kegelschnitt eine Parabel, so lassen sich drei Fälle unterscheiden.
  1. Der Punkt liegt auf der Parabel.
    
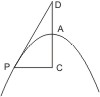
    Man fälle von ihm auf die Achse ein Loth, verlängere die Achse über den Scheitel hinaus um das durch das Loth abgeschnittene Stück und verbinde den erhaltenen Endpunkt mit dem gegebenen Punkt, so ist diese Verbindungslinie die gesuchte Tangente. I. 33.
  2. Der Punkt liegt auf der Verlängerung der Achse.
    Man schneide auf der Achse vom Scheitel nach innen zu ein Stück ab gleich dem Stück zwischen dem Scheitel und dem gegebenen Punkt, errichte in dem erhaltenen Punkt nach beiden Seiten zu ein Loth, das die Parabel in zwei Punkten trifft und verbinde diese Punkte mit dem gegebenen, so sind dies die verlangten Tangenten.
  3. Der Punkt P liegt beliebig ausserhalb der Parabel.
    
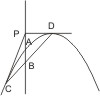
    Man ziehe von P eine Parallele mit der Achse, welche die Parabel in A trifft, schneide darauf von A nach innen zu ein Stück AB = PA ab, ziehe in A die Tangente an die Parabel und in B eine Parallele damit, die die Parabel in C und D trifft; dann sind PC und PE die verlangten Tangenten. (I. 46. I. 33.)
2. Ist der gegebene Kegelschnitt eine Hyperbel, so lassen sich fünf Fälle unterscheiden.
  1. Der gegebene Punkt P liegt auf der Hyperbel.
    
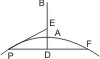
    Man suche die Achse, fälle von P darauf ein Loth PD; sind nun A und B die Scheitel, so bestimme man einen Punkt E in der Achse, so dass AE : BE = AD : BD; dann ist EP die gesuchte Tangente. (I, 34.)
  2. Der gegebene Punkt. E liegt in der Achse.
    Sind wieder A und B die Scheitel, so bestimme man in der verlängerten BA einen Punkt D, so dass AD : BD = AE : BE, errichte in D auf die Achse nach beiden Seiten zu ein Loth, das die Hyperbel in P, F trifft, dann sind PE, EF die verlangten Tangenten. (I. 34.)
  3. Der gegebene Punkt P liegt beliebig ausserhalb der Hyperbel, jedoch innerhalb des Asymptotenwinkels
    
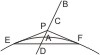
    Man ziehe von P durch den Mittelpunkt C eine Linie, welche die Hyperbel in A, ihren Gegenschnitt in B trifft; bestimme in dieser Linie einen Punkt D, so dass AD : BD = AP : BP, ziehe in A die Tangente und in D eine Parallele damit, welche die Hyperbel in E, F schneidet, dann sind PE, PF die verlangten Tangenten. (I. 47. I. 34.)
  4. Der gegebene Punkt P liegt in einer Asymptote.
    
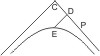
    Ist C der Mittelpunkt, so nehme man die Mitte D von CP und ziehe durch D eine Parallele mit der andern Asymptote, welche die Hyperbel in E trifft, dann ist PE die verlangte Tangente. (II. 3.)
  5. Der Punkt P liegt innerhalb des Nebenwinkels des Asymptotenwinkels.
    
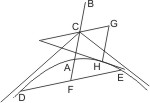
    Man ziehe von P nach dem Mittelpunkt C und parallel mit PC eine Sehne DE in der Hyperbel, verbinde deren Mitte F mit C, welche Linie die Hyperbel in A und den Gegenschnitt in B trifft, dann bestimme man die Grösse des zum Durchmesser AB gehörigen Rechtecks Q² durch die Proportion: DF² : FA · FB = Q² : AB² und ferner auf der verlängerten PC einen Punkt G dergestalt, dass CP · CG = Q² ist, ziehe endlich von G eine Parallele mit CF, welche die Hyperbel in H trifft; dann ist PH die gesuchte Tangente. (I. 38. I. 47. I. 21. Zweite Reihe von Erkl. No. 4.)
    Wenn endlich der gegebene Punkt im Scheitelraum des Asymptotenwinkels liegt, so ist die Construction einer Tangente unmöglich.
3. Sei drittens der gegebene Kegelschnitt eine Ellipse, so lassen sich zwei Fälle unterscheiden.
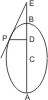
  1. Der Punkt P liegt im Umfang derselben.
    
    Fälle von P auf die Achse ein Loth PD, und wenn A, B die Scheitel der Achse sind, bestimme in deren Verlängerung einen Punkt E, so dass AE : BE = AD : BD, dann ist EP die verlangte Tangente. (I. 34.)
  2. Der Punkt P liegt beliebig ausserhalb derselben.
    
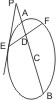
    Ziehe von P durch den Mittelpunkt C und, wenn A, B die hierdurch erhaltenen Scheitel sind, bestimme in AB einen Punkt D dergestalt, dass AD : BD = AP : BP, ziehe ferner nach Vorigem in A oder B eine Tangente und eine Parallele damit durch D, welche die Ellipse in E, F trifft, dann sind PE, PF die verlangten Tangenten. (I. 34, I. 47.)
Aufgabe 7. An einen gegebenen Kegelschnitt eine Tangente zu ziehen, die mit der Achse nach der Seite des Kegelschnitts zu einen gegebenen spitzen Winkel bildet.
1. Für die Parabel.
  Sei eine Parabel mit dem Scheitel A und der Achse AF, sowie der spitze Winkel α gegeben; man soll an erstere eine Tangente ziehen, die mit der Achse nach der Seite des Schnitts zu den Winkel DEA = α bildet.
  
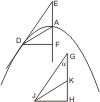
  Analysis. Ist an einer Parabel AD im Punkte D die Tangente gezogen, welche die Achse im Punkt E unter dem verlangten Winkel schneidet, und von D auf die Achse das Loth DF gefällt, so wie AD gezogen, so ist das Dreieck DEF durch zwei Winkel der Gestalt nach bestimmt, und weil EA = AF, auch der Punkt A in der Grundlinie, also der Winkel DAF gegeben.
  Construct. Trage an einer beliebigen Linie GH in H einen Rechten und in G den Winkel α an, verbinde die erhaltene Spitze J des Dreiecks mit der Mitte K von GH; trage nun an die Achse der Parabel im Scheitel A nach innen zu den gefundenen Winkel JKH nach beliebiger Seite an und ziehe in dem Durchschnittspunkt D des erhaltenen Schenkels mit der Parabel die Tangente an dieselbe, so ist dies die verlangte.
  Bew. Ist E der Schneidungspunkt der Tangente mit der Achse, DF das von D auf die Achse gefällte Loth, so ist ∆DAF ∾ ∆JKH aus zwei Winkeln, also DA : AF = JK : KH, also auch DA : AE = JK : KG und also ∆DAE ∾ ∆JKG aus 2 Seiten und dem eingeschlossenen Winkel, folglich ∠DEF = ∠JGH = α. q. e. d.
  Anm. Da der Winkel JKH nach zwei Seiten der Achse zu angetragen werden kann, so giebt es zwei Tangenten, die der Aufgabe genügen.
2. Für die Hyperbel.
  
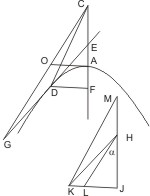
  Sei ein spitzer Winkel α und eine Hyperbel AD gegeben; man soll an diese eine Tangente ziehen, die mit der Achse nach der Seite der Hyperbel zu einen Winkel DEA gleich α bildet.
  Analysis. Ist im Punkte D einer Hyperbel eine Tangenten gezogen, die die Achse im Punkte E unter dem verlangten Winkel schneidet, und DF das von D auf die Achse gefällte Loth, C der Mittelpunkt, A, B die Scheitel, so ist nach I.37. DF² : FE · FC = r : t, und da wegen des bekannten Winkels DEF das Verhältniss DF : FE gegeben ist, ist auch durch Division DF : FC mithin der Winkel DCF gegeben. Man bemerkt ferner, dass, da die verlängerte ED die Asymptote in einem Punkt G treffen muss, der Winkel DEF oder α grösser als der halbe Asymptotenwinkel GCE sein muss.
  Construct. Errichte in einem beliebigen Punkt J auf einem Schenkel des Winkels α, dessen Scheitel H sei, ein Loth, das den andern Schenkel in K trifft, und bestimme auf der verlängerten JH einen Punkt M, so dass KJ² : JH · JM = r : t, ziehe MK und trage den Winkel KMJ an die Achse CA der Hyperbel im Punkte C nach der Seite der Hyperbel zu an, bis sein Schenkel die Hyperbel in D trifft, so ist die in D gezogene Tangente DE die verlangte. ( Anm. Die Bestimmung des Pnnktes M geschieht am einfachsten so, dass man zuerst HJ = t und dann JM = KJ² ⁄ r macht; denn dann ist in der That KJ² : JH · JM = LM · r : JH · JM = r : t.)
  Bew. Man ziehe von D die Ordinate DF und die Linie DC, so ist ∆DFC ∾ ∆KJM wegen gleicher Winkel, also: 1) KJ : JM = DF : FC; weil aber (2) KJ² : JH · JM = r : t nach Construct und (3) DF² : FE · FC = r : t nach I.37., ist KJ² : JH · JM = DF² : FE · FC, welches durch (1) dividirt, giebt KJ : JH = DF : FE, also ist ∆KHJ ∾ ∆DEF und folglich ∠DEF = ∠KHJ = α, wie verlangt war.
  Es bleibt noch zu zeigen, dass, wenn der gegebene Winkel α grösser als der halbe Asymptotenwinkel ist, die Construction immer ausführbar ist.
  Sei JHL gleich dem halben Asymptotenwinkel und werde in A auf CA ein Loth errichtet, das die Asymptote in O trifft. Nun ist CA² : AO² = t : r nach II. 3., also auch HJ² : JL² = t : r und folglich HJ² : JK² < t : r; weil nun HJ· MJ : JK² = t : r nach Construction, muss MJ > HJ und folglich MJ² : JK² > t : r, also MJ² : JK² > HJ² : JL² oder MJ : JK > HJ : JL, woraus folgt, dass der Winkel KMJ kleiner als der halbe Asymptotenwinkel LHJ ist, und in diesem Falle wird der Schenkel des an AC in C angetragenen Winkels KMJ nothwendig die Hyperbel schneiden, also die Construction ausführbar sein.
  Anm. Da der Winkel KMJ an zwei Seiten von CA angetragen werden kann, sind zwei Tangenten möglich, die der Aufgabe genügen.
3. Für die Ellipse.
  
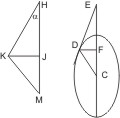
  Sei ein Winkel α = KHJ und eine Ellipse gegeben; an diese eine Tangente zu ziehen, die mit der Achse nach der Ellipse zu einen Winkel gleich α bildet.
  Analysis. Wäre DE die verlangte Tangente, DF die von D an die Achse gezogene Ordinate und DC die Linie nach dem Mittelpunkt, dann müsste DF² : CF · FE = r : t und da DF : EF durch die Winkel gegeben ist, so ist auch DF : CF, mithin der Winkel DCF bekannt.
  Construction. Mache einen Schenkel HJ des gegebenen Winkels α gleich t, errichte in J ein Loth, das den andern Schenkel in K trifft, bestimme in der verlängerten HJ einen Punkt M, so dass r : KJ = KJ : JM, ziehe KM und trage den Winkel KMJ in C an die Achse der Ellipse beliebig an; trifft nun der Schenkel die Ellipse in D, so ist die in D gezogene Tangente DE die verlangte.
  Bew. Ist DF noch die in D gezogene Ordinate an die Achse, so ist DF² : CF · FE = r : t und da auch KJ² : JM · JH = JM · r :JM · JH = r : t, ist DF² : CF · FE = KJ² : JM · JH. Weil aber ∆CDF ∾ ∆KMJ, muss DF : CF = KJ : MJ und deshalb auch DF : FE = KJ : JH, und folglich ∠DEF = ∠KHJ = α sein.
Aufgabe 8. An einer gegebenen Parabel oder Hyperbel eine Tangente zu construiren, welche mit dem durch den Berührungspunkt gehenden Durchmesser einen gegebenen spitzen Winkel bildet.
Wenn eine Parabel gegeben ist, so ergiebt sich aus dem Parallelismus der Durchmesser leicht, dass man nur die vorige Aufgabe aufzulösen hat.

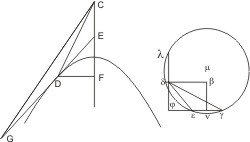
Sei eine Hyperbel AD und ein spitzer Winkel α gegeben; es soll an erstere eine Tangente gezogen werden, die mit dem nach dem Berührungspunkt gezogenen Durchmesser einen Winkel gleich α bildet.
Analysis. Wäre DE die verlangte Tangente, CD der Durchmesser nach dem Berührungspunkt, DF die von D an die Achse gezogene Ordinate, so wäre in der Figur CDF der rechte Winkel bei F, der Winkel CDE und das Verhältniss DF² : FE · FC = r : t bekannt; daraus ist aber ihre Gestalt bestimmt; denn beschreibt man über einer beliebigen Länge εγ als Sehne einen Kreisbogen, der den Winkel α als Peripheriewinkel enthält, und fällt von einem beliebigen Punkt des Kreises δ ein Loth δϕ auf die verlängerte γε so ist, wenn λ der zweite Schneidungspunkt dieses Lothes mit dem Kreis ist, δφ² : φε · φγ = δφ² : δφ · φλ = δφ : φλ, weshalb sich die Lage des Lothes aus dem gegebenen Verhältniss δφ² : φε · φγ leicht bestimmen lässt.
Construction. Man ziehe eine gerade Linie εγ und beschreibe darüber einen Kreisbogen, der den Winkel α als Peripheriewinkel enthält, schneide auf einer andern beliebigen geraden Linie von einem Punkt G aus das Latus rectum und transversum nach derselben Seite zu den Punkten H und J ab, halbire HJ in K, fälle vom Mittelpunkt μ des über εγ beschriebenen Kreisbogens ein Loth μν auf εγ/ und theile es durch den Punkt β, so dass μν : βν = KG : HG, ziehe von β eine Parallele mit εγ welche den Kreis in δ trifft, ziehe δγ und trage den erhaltenen Winkel δγε an CA im Punkte C an, bis sein Schenkel die Hyperbel in D trifft, so ist die in D gezogene Tangente DE die verlangte.
Bew. Man ziehe noch δε und das Loth δφ von δ auf γε, welches verlängert den Kreis zum zweiten Mal in λ trifft, ferner das Loth DF von D auf die Achse und im Scheitel A die Tangente, die eine Asymptote in L trifft. Nun ist zunächst zu zeigen, dass der Schenkel des an CA angetragenen Winkels δγε die Hyperbel nothwendig treffen muss. Es ist (1) CA² : LA² = t : r (II. 3), und da μβ : βν = ½ · (t - r) : r, 2 · μβ oder λδ : δφ = t - r : r also auch λφ : δφ = t : r, oder, wenn das erste Verhältniss mit δφ erweitert und φγ · φε statt λφ · δφ gesetzt wird, φγ · φε : δφ² = t : r und folglich (2) φγ² : δφ² > t : r, welches mit (1) verglichen zeigt, dass φγ : δφ > CA : LA, folglich Winkel δγφ kleiner als LCA ist, und also schneidet der Schenkel des im CA angetragenen Winkels δγφ nothwendig die Hyperbel. Nun bleibt zu zeigen, dass die im Schneidungspunkt D gezogene Tangente DE mit dem Durchmesser CD einen Winkel gleich α bildet. Es ist ∆DFC ∾ ∆δφγ wegen gleicher Winkel, und da DF² : FE · FC = r : t nach I. 37 und δφ² : φγ · φε = r : t, wie oben gezeigt ist, also (3) DF² : FE · FC = δφ² : φγ · φε, und aus obiger Aehnlichkeit (4) DF : FC = δφ : φγ, also (3) durch (4) dividirt DF : FE = δφ : φε, folglich Winkel FDE = φδε, welches von den gleichen Winkeln FDC, φδγ subtrahirt, giebt EDC = εδγ und also gleich α. w. z. b. w.
Lehrsatz 44. Der spitze Winkel, den eine Tangente an einer Ellipse mit dem nach dem Berührungspunkt gezogenen Durchmesser bildet, ist nicht kleiner als der Nebenwinkel des Winkels, den die von den Endpunkten der grossen Achse nach einem Endpunkt der kleinen gezogenen Linien bilden.

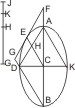
Sei eine Ellipse mit dem Mittelpunkt C, der grossen Achse AB und der halben kleinen CD gegeben, AD und BD und in einem beliebigen Punkt E des Umfangs sowohl der Halbmesser EC als auch die Tangente gezogen, die die verlängerte Achse BA in F, die verlängerte BD in G trifft, so wird behauptet, dass der Winkel CEG nicht kleiner als Winkel GDA ist.
Sei erstens BD ∥ CE, dann ist, weil AC = BC, wenn H der Durchschnitt von AD und CE ist, auch AH = DH und folglich FG ∥ AD (Umkehr. von I. 47.), also Winkel CEG = GDH.

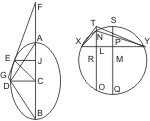
Sei ferner BD nicht parallel CE und noch von E an die Achse die Ordinate EJ gezogen. Nun ist Winkel ECJ ungleich Winkel DBC, also auch DC² : CB² ungleich EJ² : CJ², und da DC² : CB² = EJ² : CJ · JF, ist CJ · JF ungleich CJ², also JF ungleich CJ. Sei nun ein beliebiger Kreis und darin eine Sehne XY gegeben, so dass der zu XY gehörige stumpfe Peripheriewinkel gleich ADB ist, ferner von der Mitte des Bogens S ein Durchmesser SMQ gezogen, der XY in P schneidet. Nimmt man nun in XY einen Punkt L, so dass XL : LY = CJ : JF und zieht in L lothrecht gegen XY die Sehne NO, deren Mitte R ist, so ist zunächst leicht zu zeigen, dass NL² : XL · LY < SP² : PX², also kleiner als DC² : AC · CB oder als EJ² : CJ · JF ist. Denn NL² : XL · LY = NL² : NL · LO = NL : LO = NR - RL : NR + RL und da in letzterem Verhältniss das Vorderglied kleiner als das Hinterglied ist, wird es vergrössert, wenn beide Glieder um dasselbe Stück wachsen, also wenn in beiden SM statt NR gesetzt wird, also hat man, da RL = PM ist, NL² : XL · LY < SM - NP : SM + MP, d. h. als SP : PQ oder SP² : SP · PQ oder SP² : XP². Nimmt man also in der verlängerten LN einen Punkt T, so dass TL² : XL · LY = SP² : PX² = EJ² : CJ · JF, so ist ∆XTY ähnlich ∆CEF; denn da XL : LY = CJ : JF, ist XL² : XL · LY = CJ² : CJ · JF und da TL² : XL · LY = EJ² : CJ · JF, ist durch Division XL² : TL² = CJ² : EJ², also ∆XLT ähnlich ∆CJE und auf gleiche Weise ∆YLT ähnlich ∆FJE. Mithin ist, da ∠XTY kleiner als ∠XNY, letzterer aber gleich ADB, auch ∠CEF kleiner als ADB und sein Nebenwinkel GEC grösser als ADG. w. z. b. w.
Aufgabe 9. An eine Ellipse eine Tangente zu ziehen, die mit dem nach dem Berührungspunkt gezogenen Durchmesser einen gegebenen spitzen Winkel bildet, welcher jedoch nicht kleiner sein darf als der, den zwei Linien von den Endpunkten der kleinen Achse nach einem Endpunkt der grossen gezogen bilden.

Sei eine Ellipse mit der grossen Achse AB, der kleinen DK, dem Mittelpunkt C und ein spitzer Winkel α nicht kleiner als der Winkel DAK gegeben, man soll eine Tangente GEF an die Ellipse ziehen, so dass der spitze Winkel GEC gleich α ist.
1. Sei α = DAK. Man ziehe AD, halbire es in H, ziehe CH, bis es die Ellipse in E trifft, so ist die durch E mit AD gezogene Parallele die verlangte Tangente.
1. Sei α > DAK, also sein Nebenwinkel β < ADB. Man zeichne einen beliebigen Kreis und darin eine Sehne XY, so dass der dadurch gebildete kleinere Bogen den Peripheriewinkel β enthält, ziehe von der Mitte S dieses Bogens einen Durchmesser SPMQ und bestimme in SP einen Punkt Z, so dass ZP : ZM = r : ½ · (r + t), ziehe durch Z eine Parallele mit XY, die den Kreis in N trifft, trage den Winkel NXY an die Achse CA im Punkte C an; trifft nun der Schenkel die Ellipse in E, so ist die Tangente in E die verlangte.
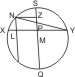
Beweis. Ziehe noch von N aus die Sehne NLO parallel mit SQ.
Da nach Voraussetzung der Winkel β = XSY kleiner als ADB ist, ist XP · PY : SP² oder PQ : SP < AC · BC : DC², d. h. als t : r, mithin, wenn man auf beiden Seiten 1 addirt und die Vorderglieder halbirt, ½ · (PQ + SP) : SP < ½ · (t + r) : r, und da ZM : ZP = ½ · (t + r) : r, ist also SM : SP < ZM : ZP oder, wenn man auf beiden Seiten 1 subtrahirt, PM : SP < PM : ZP, also SP > ZP; folglich muss die durch Z gezogene Parallele den Kreis nothwendig schneiden und die Construktion immer möglich sein. Nun folgt aus ZP : ZM = r : ½ · (t + r) leicht ZP : 2 · ZM - ZP = r : t, also auch NL : LO oder NL² : XL · LY = r : t; da aber EI² : CI · IF = r : t und ∆XNL ähnlich ∆CIE, also NL : XL = EI : IC, folgt durch Division auch NL : LY = EI : IF, also ∆NLY ähnlich ∆EIF und Winkel LNY = IEF, also auch Winkel β = XNY = CEF. w. z. b. w.