Die Näherung für den Kreisumfang

Die recht genaue Näherung der Zahl π wird Archimedes von Syrakus zugeschrieben. Er nutzte dem Kreis ein- bzw. umgeschriebene Polygone, denn deren Seitenlänge konnte er berechnen.

Eingeschriebenes Polygon

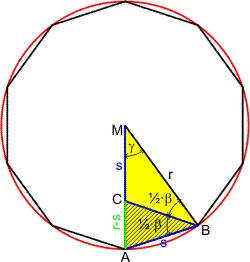
Im Beispiel ist ein zehnseitiges, regelmäßiges Polygon dem Kreis mit dem Radius r = 1 eingeschrieben, sodass die Ecken auf dem Kreisumfang liegen. Verbindet man dem Kreismittelpunkt M mit den beiden Ecken eier Seite des Polygons, so entsteht ein gleichschenkliges Dreieck ABM, mit den beiden Schenkeln MA = MB = r. Die Basis des Dreiecks ist die Polygonseite AB = s.

Zeichnet man nun die Winkelhalbierende BC des Winkels β bei B, so entstehen zwei gleichschenklige Dreiecke ABC und BCM, die die Seite BC gemeinsam haben und einen gleichen Winkel (γ = ½·β). Die Dreiecke ABC und ABM sind ähnlich (sie haben eine gemeinsame Seitenlänge s und die den Basen gegenüberliegenden Winkel sind gleich, denn der Winkel γ = ½·β =  1 ⁄ 10 · 360° = 36°). Die Seiten haben die Längen AB = BC = AM = r. Damit ist AC = r - s.

Aus der Ähnlichkeit der Dreiecke ABC und ABM folgt, dass die Verhältnisse entsprechender Seitenlängen gleich sind. Also: eine der gleichlangen Seiten im Dreieck AB = s bzw. BM = r zur jeweiligen Basis AC = r - s bzw. AB = s. Wie erhalten die Beziehung: r : s = s : (r - s). Diese Gleichung kann man nach s auflösen und erhält:

Setzt man in diese Formel r = 1, erhält man für das Verhältnis von Kreisumfang zu -durchmesser π = 3,09.

Umschriebenes Polygon

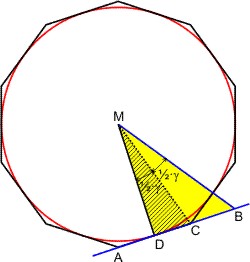
Um in diesem Falle die Länge der Polygonseite berechnen zu können, konstruiert man wieder Dreiecke. Diesmal steht der Radius r allerdings auf der Mitte einer Polygonseite senkrecht, d. h. die ist eine Tangente des Kreises. Die Tangente verlängert man und zieht eine weitere Speiche des Kreises bis zum Schnittpunkt B. Die Verbindungslinie des Mittelpunktes M mit einer Ecke C des Polygons halbiert den Winkel γ. Nun hat man zwei rechtwinklige Dreiecke DBM und DCM, die eine Kathete DM gemeinsam haben.

Nach dem 6. Buch Euclids, Satz 3, ist nun DC :BC = DM : BM. Leider hilft das nicht weiter. Wir kennen nur zwei Größen des Dreiecks: die Seite MD und den Winkel bei M — und zur eindeutigen Bestimmung eines Dreiecks braucht es drei. Gehen wir zu den Quellen [1].

Archimedes hatte umfangreiche Messungen am Kreis und an Quadraten und Dreiecken vorgenommen. Er postuliert im Buch "Kreismessungen" [1] einen Kreis, dessen Fläche etwas kleiner ist als die eines Dreieck mit dem Kreis­radius als der einen Kathete und dem Kreisum­fangs als der anderen. Dem Kreis umschreibt er ein Quadrat und verdop­pelt in einem Gedankenexperiment die Eckenzahl (also zum 8-, 16-, 32-, … bis zum 96-Eck) um einen Grenzwert für das Verhältnis von Kreisumfang zu Kreisdruchmesser (π) zu finden.

Archimedes behauptet nun (Satz 2 im Buch über Kreismessung), die Fläche des Kreises verhält sich zu der des umschriebenen Quadrats "sehr nahe wie 11 : 14".

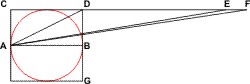Und er überprüft das mit Hilfe einer Figur. Dabei soll das Dreieck ACF die Fläche enthalten, die die Kreisfläche annähert. Der Abstand DE ist 2 · CD, und der Abstand EF = 1 ⁄ 7 · CD. (Diese Angabe stammt offensichtlich aus den Messun­gen: die Länge der Kathete CF ist 3 1 ⁄ 7 = 3,1428 mal der Kreisradius! π = 3,1416.) Die Fläche des Dreiecks ACE ist F_ACE = ½ · AC · AE = 21 ⁄ 7 = 3, die des Dreiecks ACD ist F_ACD = ½ · AC · AD = 7 ⁄ 7 = 1 (Archimedes hatte ja das Flächenverhältnis 11 : 14 postuliert!), und das Dreieck AEF hat die Fläche F_AEF = 1 ⁄ 7 (wegen der Konstruktion des Dreiecks).

Die Fläche des Dreiecks ACF verhält sich zur der des Dreiecks ACD mithin F_ACF : F_ACD = 22 : 7. Da vier Dreiecke ACD die Fläche des Quadrats F_Quad bilden, verhält sich die Fläche des Dreiecks ACF zur Quadratfläche F_ACF : F_Quad = 22 : 28 = 11 : 14. Der Umfang des dem Kreis umschriebenen Quadrats ist also ein Maß für die Kreisfläche. Also ist 3 1⁄7  eine Näherung für π.

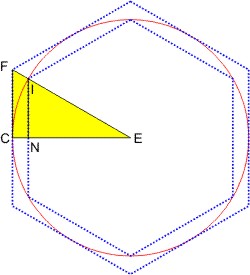
Um sich der Verhältniszahl π weiter zu nähern, vermaß Archimedes den Umfang der Kreises. Er kommt zu dem Schluß, dass 3 1⁄7 = 3,1428 > π > 3 10⁄71 = 3,1408. Die untere Schranke beweist er mit Überlegungen zu Verhältnissen in der nebenstehenden Figur. Er konstruiert ein rechtwinkliges Dreieck FCE (gelb) mit einer Kathete CE = r und der Hypotenuse EF = 2·CF. Der Winkel bei E im gelben Dreieck ist ⅓ eines rechten Winkels. In diesem Dreieck gilt nach Pythagoras
EF² = (2·CF)² = CF² + r².
oder — aufgelöst — CF = r·√3.
Da Archimedes einen Wert für das Verhältnis CF : r finden wollte (CF ist eine halbe Seite eines Sechsecks und dessen Umfang konnte er berechnen), suchte er einen Zahlenwert für 3·r², der etwas größer ist als eine Quadratzahl. Mit r = 153 hatte er eine für seine Zwecke optimale Zahl gefunden, denn 3·153² = 70.227 = 70.225 + 2 = 265² + 2.
Aus der Konstruktion des gelben Dreiecks folgt FE : FC = 2 : 1 = 306 : 153. Und FE² : FC² = 93.636 : 23.409.

1. Ernst Nizze (Übers.): Archimedes von Syrakus vorhandene Werke, Stralsund 1824.
2. Mathematik-Ratgeber (Herausg. W. Gellert), VEB Bibliographisches Institut Leipzig, 1984.
3. Helmuth Gericke, Mathematik in Antike und Orient, Springer-Verlag Heidelberg Berlin, 1984.
4. David E. Joyce, Euclid's Elements, Math and Computer Science, Clark University, Worcester, MA, USA.
5. Joh. Jos. Ign. Hoffmann: Die geometrischen Bücher der Elemente des Euclides; als Leitfaden zum Unterrichte in der Elementar-Geometrie, Mainz, 1829.