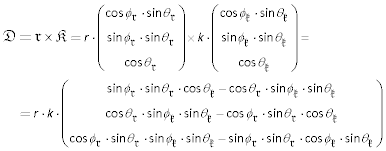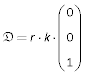Vektoren werden auf dieser Seite mit fetten Buchstaben in der Frakturschrift bezeichnet. Die Kodierung erfolgt mit Unicode-Glyphen 1D565 bis 1D59F. Diese werden mit aktuellen Versionen vieler Browser dargestellt. Nicht dargestellt werden sie mit Windows® und iOS® Versionen von Safari®.

Drehbewegungen

Ein wichtiges Konzept, das Segler kennen sollten, ist die Physik der Drehbewegung. Sie ist die Grundlage zum Verstehen z.B. des Schraubeneffekts und der der Entstehung von Zyklonen (Tief­druck­ge­biete). Die physikalischen Größen sind der Bahndrehimpuls und das Drehmoment.

Definition der Drehbewegung

Der Hebel

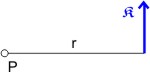Hebel Der Hebel ist ein Körper, der im Punkt P unterstützt wird. Im Abstand r vom Unterstützungspunkt wirkt eine Kraft 𝕶, was zur Folge hat, dass sich der Hebel in Richtung 𝕶 um P dreht. Jeder kennt das vom Schraubenschlüssel. Je größer die Kraft 𝕶 oder je länger der Hebel (Abstand r) ist, desto leichter löst sich die Schraube.

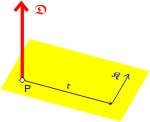Hebel Dieser Zusammenhang wird quantitativ dargestellt in der Formel

  • 𝕯 = 𝖗 × 𝕶
Das Produkt aus Hebellänge und Kraft nennt man Drehmoment im Bezug auf die Achse. Da 𝖗 und 𝕶 gerichtete Größen (Vektoren) sind, und das Vektorprodukt angewandt wird, ist das Drehmoment eine Größe, die senkrecht auf der Ebene steht, in der der Hebel- und der Kraftvektor liegen.

Mit den Regeln für das Vektorprodukt kann man das Senkrechtstehen des Drehmoments auf der Hebelebene zeigen. Dazu werden die Vektoren in räumlichen Polarkoordinaten dargestellt.

  • Formel
Das ist etwas unübersichtlich. Legen wir also den Hebelarm 𝖗 auf die x-Achse, also ist ΔΦ𝖗 = 0° und sin Φ𝖗 = 0. Lassen wir den Kraftvektor 𝕶 senkrecht auf dem Hebelarm stehen, so ist ΔΦ𝕶 = 90° und cos Φ𝕶 = 0. Da beide Vektoren nun in der x-y-Ebene liegen, ist Δθ𝖗 = Δθ𝕶 = 90°, und somit cos θ𝖗 = cos θ𝕶 = 0. Damit vereinfacht sich der Matrixausdruck für das Drehmoment zu:
  • Formel
𝕯 hat also nur eine Komponente in Richtung der positiven z-Achse, und die Länge des Vektors ist
  • |𝕯| = r · k.
Die Richtung entspricht der rechten Hand Regel, die Länge der Formel ohne Vektoren.

Das Kräftepaar

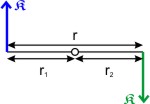Drall Greifen an einem Körper zwei parallele aber entgegengesetzt wirkende gleich große Kräfte 𝕶 im Abstand r an, so wirken auf den Körper zwei Drehmonente 𝕯1 = 𝖗1 × 𝕶 und 𝕯2 = 𝖗2 × 𝕶. Da sich die beiden Kräfte 𝕶 nicht zu einer resultierenden Kraft zusammensetzen und wegen r1 + r2 = r, ergibt sich nur ein Drehmonent 𝕯 = 𝖗 × 𝕶, das von der Lage der Achse unabhängig ist.

Der Drehimpuls

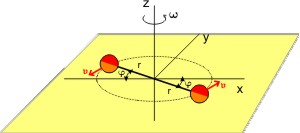Drall Analog zum Impuls 𝖕 = m · 𝖛 eines gleich­mäßig linear bewegten Körpers mit der Masse m kann man einen Drehimpuls eines mit gleich­mäßiger Geschwindigkeit rotierenden Körpers definieren.

Eine starre Hantel rotiere in der x,y-Ebene um die z-Achse, sodaß der Schwerpunkt der Han­tel im Ursprung des Koordinatensystems liege. Der Geschindigkeitsvektor 𝖛 der Körper liegt dann auch in der x,y-Ebene und er ist abhängig vom Abstand r von der Drehachse und von der Änderung des Winkels φ

  • 𝖛 = Δx ⁄ Δt
  • Δx ist der Bruchteil des Kreisbahnumfangs, der dem der Winkeländerung am Vollumfang entspricht:
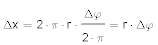
  • Formel
  • 𝖛 = (r ·Δφ) ⁄ Δt.
  • mit der Winkelgeschwindigkeit ω = Δφ ⁄ Δt
  • 𝖛 = r · ω
𝖛 = Δx ⁄ Δt. Der Geschindigkeitsvektor 𝖛 ändert seine Richtung allerdings abhängig vom Winkel φ.

Valid HTML 4.01 © Rainer Stumpe URL: http://www.rainerstumpe.de