Demonstra, quod repraesententur hae ellipticae proprietates in orbita planetae, quae ex illis librationibus nascitur.
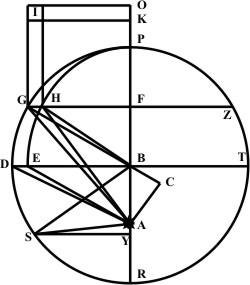
Describatur igitur legibus hactenus traditis nova figura, centro scilicet B circulus PDR, quem tangere debeat ellipsis, cujus sit longior diameter PR, et in ea A focus seu locus Solis. Agatur ipsi PR perpendicularis per B, quae sit DT, erit in ea diameter brevior. Et quia BA eccentricitas est dimidium librationis, tanta igitur competet perfecto quadranti; planeta igitur, in lineam DB incidens, distabit a Sole minus quam in P, differentia BA, distabit igitur quantitate BP, quare intervallum aequale ipsi BP ex A extendatur in DB, sitque terminus ejus E. Planetae igitur orbita secabit DB in E.
Rursum assumatur arcus circuli PG ejusque sinus seu ordinatim applicata GFZ et sinus versus PF. Fac igitur ut BP ad PF, sic BA, dimidiam librationem, ad partem ipsi PG competentem, qua ablata ab AP, residuum ex A in GF extendatur incidatque terminus in H. Dico, ut DB est ad BE, sic etiam esse GF ad FH. Scribantur enim quadrata, super GF quidem GIOF, super HF vero HK, ut sit gnomon HIK; deinde G cum A. et cum B connectatur, et ex A perpendicularis in GB continuatam exeat, quae sit AC.
Dico initio, quadratum ab AC aequale esse gnomoni HIK.
Nam quia factum est, ut BP ad PF, sic BA ad differentiam linearum AP, AH, quare etiam ut PB ad BF, sic BA ad excessum, quo AR adhuc superat BP. At etiam ut PB seu GB ad BF, sic AB ad BC, quia GFB et ACB rectangula aequales habent angulos GBF et ABC ad verticem. Ergo BC aequat portionem, qua AH superat BP; at et CG superat BP, hoc est BG, eadem portione BC, quare aequales sunt GC et HA. Sed quadratum rectae GC una cum quadrato perpendicularis AC juncta aequant quadratum rectae GA. Ex altera vero parte quadratum ab AF cum quadrato ab FG junctim aequant quadratum ejusdem GA. Ergo aequalia sunt duo quadrata a GF et ab FA juncta junctis quadratis a GC et a CA. Aequalis igitur auferantur, hinc quadratum ab GC, inde quadratum ab aequali linea AH, id est duo quadrata et ab AF et ab FH, scilicet HK: restat hic quadratum ab AC, illic gnomon HIK.
Hinc jam facile pertexitur reliquum demonstrationis propositae.
Nam ut unus sinus GF ad suam perpendicularem AC, sic omnes alii ad suas ex A. Ut igitur quadratum sinus GO ad quadratum ab AC, id est ad gnomonem HIK, ita omnium sinuum quadrata ad suos gnomones: quare etiam ablatis gnomonibus, ut unius sinus GF quadratum GO ad quadratum HK ipsius FH, a distantia HA planetae a Sole determinatae, ita uniuscujusque sinus quadratum ad minoris a sua distantia determinatae quadratum. Quorum vero quadrata sunt inter se proportionalia, illa ipsa ut latera sunt proportionalia inter se. Ut igitur GF ad FH, portionem ab AH terminatam, sic quilibet sinus, ut DB ad BE, portionem a sua AE determinatam: quae ratio est genuina ellipseos.
Altera proprietas ellipsis per se patet.
Ad praescriptum enim legum librationis (quia scilicet in quadrante orbitae PE consumi debet dimidia libratio ipsi BA aequalis) residuae BP aequalem ex A in DB extendimus, scilicet AE. Nam quia A focus unus, si ipsi BA statuatur aequalis in BP ex B extensa, designabitur focus alter, cujus ab E distantia erit aequalis ipsi AE, et junctae aequabunt diametrum: quod fit in ellipsi.
Zeige, was diese elliptischen Größen in der Planetenbahn repräsentieren und welche von ihnen aus der Libration resultieren.
Um die Formeln bis hier her zu beschreiben, zeichnen wir eine neue Abbildung, der Mittelpunkt des Kreises PDR ist selbstverständlich B, und er fällt mit dem Mittelpunkt einer Ellipse zusammen, deren längerer Durchmesser PR ist, und in ihrem Brennpunkt A steht die Sonne. Eine Senkrechte zu PR in B, die DT sei, auf der sei der kürzere Durchmesser [der Ellipse abgetragen]. Und weil die Exzentrizität BA die Hälfte der Libration ist, die ist so große weil sie einem vollständigen Quadranten entspricht; deshalb ist der Planet, der auf der Linie DB steht, weniger weit entfernt [von der Sonne in A] als in P, der Unterschied ist BA, er ist daher um die Länge BP entfernt, welche Entfernung selbst gleich ist BP von A nach DB abgetragen, und der Endpunkt davon ist E. [Anm.: Die Entfernung eines Punktes im Nebenscheitel der Ellipse vom Brennpunkt ist gleich der großen Halbachse BP.] Die Planetenbahn schneidet daher DB in E. Wird andererseits der Kreisbogen PG [für den Planetenort] auf GFZ angenommen, ist sein Sinus gleich PF. Wie sich also BP zu PF verhält, oder BA, entspricht der Hälfte der Libration, zu dem vorgegebenen PG selbst, was von AP abgezogen, [eine Strecke] ergibt, die von A aus nach GF abgetragen wird und in H endet. Ich sage, wie sich DB zu BE verhält, so verhält sich auch GF zu FH. Wird deshalb ein Quadrat errichtet über GF, wie GIOF, über HF wie HK, dann sei HIK das Gnomon; dann wird G mit A und mit B verbunden, und in A das Lot auf das verlängerte GB errichtet, welches AC sei.
Ich sage zunächst, dass das Quadrat von AC gleich ist dem Gnomon HIK.
Denn es ist eine Tatsache, wie [sich] BP zu PF [verhält], so [verhält sich] PB zur Differenz der Strecken AP und AH [und] wie BA zum Überschuß, um den AR bisher BP übertrifft. Weiterhin [verhält sich] PB oder GB zu BF wie AB zu AC, weil die [Dreiecke] GFB und ACB rechtwinklig, und die Winkel GBF und ABC an der gemeinsamen Spitze gleich sind. [Anm.: Es handelt sich um "Scheitelwinkel"; zusammen mit dem rechten Winkel in beiden Dreiecken sind sie "ähnlich" (da die Winkelsumme im Dreieck 180° beträgt, stimmen sie in allen drei Winkeln überein!), und das Verhältnis der Hypothenusen GB bzw. AB ist wie das der Katheten BF bzw. AC.] Also gleicht BC dem Verhältnis, um welches AH BP übersteigt; weiterhin übersteigt CG auch BP um BG, um den Anteil BC, wodurch GC und HA gleich sind. Aber das Quadrat der Strecke GC zusammen mit dem Quadrat der Senkrechten AC ist gleich dem Quadrat GA. [Anm.: Pythagoras: Die Summe der Kathetenquadrate ist gleich dem Hypotenusenquadrat.] Andererseits sind die Quadrate von AF und FG zusammen ebenfalls gleich dem Quadrat der gleichen [Strecke] GA. Also sind die die beiden Quadrate von GF und von FA verknüpft mit den Quadraten von GC und von CA. Diese Gleichsetzungen kann man weiterführen: ausgehend vom Quadrat von GC, oder vom Quadrat der Strecke AH, es sind die beiden Quadrate von AF und von FH, selbstverständlich HK: es verbleibt dieses Quadrat von AC, jenes Gnomon HIK.
Ab hier ist es einfach, den Rest der These zu zeigen.
Denn wie der eine Sinus GF zu seiner Senkrechten AC, so alle anderen zu [den Linien] aus A. Wie deshalb das Quadrat des Sinus GO zum Quadrat über AC, so verhält es sich zum Gnomon HIK, und ebenso alle Sinusquadrate zu ihren Gnomonen: warum also die Gnomone anwenden, wenn ein Sinus GF [multipliziert mit dem] Quadrat GO verhält wie das Quadrat HK oder FH, um die Entfernung HA des Planeten von der Sonne zu bestimmen, auf diese Weise mit einem einzigen Sinus zum Quadrat GO zum Quadrat seiner kleineren von der Entfernung zu bestimmen. Weil die ersten Quadrate zu einander proportional sind, sind auch die verbundenen zu einander proportional. Wie also GF zu FH, der Teil der durch AH abgeschlossen ist, so jeder beliebige Sinus, wie DB zu BE, der Teil von seinem AE abgeschlossen: dieses Verhältnis gehört zur Ellipse.
Andere Eigenschaften der Ellipse.
Um die gleiche Formel der Libration fortzuschreiben (die selbstverständlich beim Fortschreiten im Quadranten PE des Umlaufes die Libration verringert bis sie gleich BA ist) für die Reste von BP verlängern wir von A aus nach DB, was selbstverständlich AE ergibt. Denn weil A der eine Brennpunkt ist, wenn BA selbst gleich gesetzt wird von B aus in BP, was als der andere Brennpunkt festgesetzt ist, dessen Abstand von E gleich ist AE, und die Verbindungen mit dem Durchmesser ausgeglichen werden: das passt in die Ellipse.