Libri V.

Pars Altera.

De Terminis Astronomicis & Calculo, Ex Orbita Eccentrica Orientibus.

Quomodo appelatur Orbita cuiusque Planeta?
Appelatur veteri voce Eccentricus subaudi, Circulus. Et si enim orbitæ sunt Ellipticæ, ut hic PERI quæ habent duo quasi centra A, L quæ physice Focos dicimus, & in eorum altero A Sol ipse ut centrum mundi, inest: tamen etiam punctum inter focus medium, ut B a scriptoribus Conicis centrum figuræ, peculiati iuro dicitur: & præterea ipsi figure circulus perfectus PDR metieati causa circumscribitur, centro B diverso a centro mundi A.

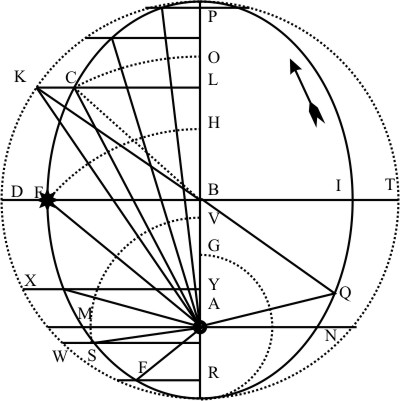
Quod nomen habet in Astronomia diameter Ellipseos longior PR?
Dicitur linea Apsidum, quia cum ducatur per centra A mundi & B orbitæ sectionibus cum orbita monstrat P summam apsidem, & R imam.

Unde dicitur summa & ima Apsis, & quod aliud habent nomen?
Vox Apsis est a rotis ducta, sunt enim puncta Eccentrici, illud P remontissimum ab A Sole, hoc R proximum illi. Sed in Geometria, ratio significationis sit evidentor. Vox enim Apsis a tangendo est nuncupata, & vero in PR punctis circulus mensor tangit Orbitam Ellipticam.
Græcam vocem Apsis Apsides latinæ versions Arabicorum librorum exprimunt per voces Aux, Auges: quasi Arabes Græcum Psi in Xi convertissent. Affirmavit tamen mihi quidam Arabicæ linguæ cognitionem iactans, voce Augh significati altitudinem.
Libro sexto, puncta ista in planetis primariis Aphelium dicentur & Perihelium, in Luna Apogæum & Perigæum.

Qua necessitas cogit, pro circulari itinere planeta, a veteribus credito: supponere Ellipticum id est, deficiens a circulo, & in eo longiorem diametrum: in que illa ipsa Solem statuere?
Utrumque horum demonstratum est observationibus & demonstration certissima, in Comm. demotibus stellæ Martis: usurpatumque libro IV fol 453 454 in schematibus, & fol 540 577 etiamque libro hoc quinto parte prima. Nisi ergo supponeremus ista, nunquam repræsentatemus Observationes.

Quibus nominibus inter se distinguantur semisses Eccentrici ab hæc linea constitute?
Alter semissis PER vel PDR descendens vel prior semicirculos dicitur, alter RIP vel RTP ascendens vel posterior.

Quid est Eccentricitas?
Græca voce εχχειτριτης, est linea connectens centra A mundi (seu corporis circa quod ordinatur motus) & B Eccentrici: scilicet AP pars linea Apsidum PR.

Quod est nomen lineis excentro corporis, circa quod motus ordinatur, in Orbitam Eccentricam edcutu?
Græce dicuntur αποτηματα. Latine intervalla seu distantiæ, in versionibus Arabicorum, dicuntur longitudines, ut AP, AC, AE, AM, AS, AF, AR, AN, AQ, &c.

Quæ sunt insigniores ex his longitudinibus?
Longitudo longior in arabicis, seu distantia aphelia vel apogæa AP, longitudo brevior seu distantia perihelia aut in Luna perigæa, AR, et longitudo media, quæ est medium arithmeticum inter longiorem et breviorem; quarum quæ est in semicirculo descendenti, puta AE, prima longitudo media dicitur, quæ in ascendenti, ut AI, secunda.

Quid praterea significant longitude media?
Metonymice sumitur pro illis punctis orbitæ, quæ obtinent mediocrem a Sole distantiam, ut E, I, quæ scilicet quadrante seu 90 gradibus ab apsidibus distant ante vel retro. Quandoque etiam sumitur pro puncto ipsius zodiaci, quod quadrante abest ante vel retro a loco zodiaci, in quem linea apsidum producta incidit.
Ubi notandum et cavendum, quod in hunc gradum zodiaci, qui longitudo media dicitur, non ipsa linea AE ejusdem nominis producta incidat, sed potius BE ex centro, vel ei parallela AM, utpote quæ cum PR apsidum linea rectos angulos formant.

Quod nomen est differentia inter longitudinem, seu distantiam mediam, & quamcuncque aliam?
Differentia hæc libratio planetæ dicitur, quia tota libratio, ut in motu lancium libræ, tarda est ab initio, cum planeta distat a Sole longissime, et in fine, cum fit Soli proximus; velox in medio.
In schemate, quia AP est longissima distantia, AR brevissima, transferatur igitur AR in lineam AP extendaturque ex A in G, ut tota libratio in unica linea AP veluti quiescente ob oculos poni possit, que erit PG, dupla eccentricitatis BA. Tarda igitur est hæc libratio circa P et G, quando scilicet planeta est vel in P vel in R, velox circa H, quando planeta seu linea AH est in AE vel AI translata.

Dixisti, circulum circumscribe Orbita, metiendi causa, dic quot nominibus ille conducat ad metiendam hanc Orbitam?
Quatuor nominibus: 1. Circulus hic denominat et discernit arcus orbitæ ellipticæ. Ut PC arcus accipit et nomen et determinationem suam ab arcu PK. 2. Circulus prodit mensuras librationum planetæ et sic format longitudines intervallorum planetæ et Solis. Ut AC vel AO determinatur arcu PK seu ejus complemento KD, quia is docet quantitatem librationis HO addendam ad semidiametrum AH. 3. Circulus exhibet etiam mensuram temporis, quod planeta consumit in quolibet arcu suæ orbitæ ellipticæ. Ut per arcum PK discimus quamdiu planeta movetur in PC arcu. 4. His inventis potest etiam indagari angulus ad Solem, quem arcus orbitæ subtendit. Ut sine arcu PK noto, ignorata AC, nequit inveniri angulus CAP.

I. De Nominatione.

Quomodo circulus denominat & discernit arcum Ellipseos, & quibus mediis, & quare?
Cum elliptica circumferentia te ipsa geometrice nequeatin partes æquales dividi, partesve constitutæ, a numero denominati: circulus igitur, Ellipsis loco, dividitur in partes æquales, ab Apsidibus initio facto: & a divisionum punctis ducuntur perpendiculars in lineam Apsidum, secants Ellipsia. Arcus igitur circuli, aphelium inter & unamquamque perpendicularem, nomen dat arcui Elliptico, inter eosdem terminus intercepti, accomodans illi suum numerum graduum & minutorum.
Sit PK gr 50 0 pr KL perpendicularis in PR secans Ellipsin in C. Ergo & arcem Ellipseos PC dicitur esse Graduum 50.0 pr.

Atqui falsum est nomen, cum non sit tantus arcus Ellipseos, neque respect circuli, neque respect sua totius orbita Elliptica?
Nihil hoc turbat, nihil est enim, in præsentia quidem, nisi nomen: & nomen quidem non mensuræ apparentis, sed determinationis & resectionis Geometricæ: ne copus est sciri genuinam longitudine, ipsius arcus Elliptici, veluti ad mesam ad decempedam: dummodo postea sciamus, hic ipse arcus Ellipseos sic determinatus, quantum angulum faciat apud centrum Solis, & quamdiu planeta commoretur in eo. Quid? Quod prima huius libri V parte demonstro, arcum Ellipseos, si non longitudine, at saltem potestate, tantum esse.

Quomodo perpendiculars ista, sectrices Ellipseos appelantur?
In circulo, dicuntur sinus arcuum circuli, inceptoru ab Aphelio: in Ellipsi, generis voce dicutur ordinatim applicatæ, puta ad axem. Ut hic KL est sinus arcus KP. CL est ordinatim applicate.
In specie vero, illa quæ per centrum figuræ ducitur, ut EBI diameter brevior, seu figuræ latus rectum dicitur. Possumus uti Græca voce Diacentros. Quæ denique; per centrum solis traiicitur ut MAN nomine caret, licet sit inter præcipuas. Dicatur novo vocabulo Dihelios.

Quodnam est officium illarum perpendicularium, Diacentri & Dihelii?
Dividunt orbitam in partes, superiorem & inferiorem, illa quidem in æquales, sed temporis & apparentiæ inæqualis: hæc in partes quidem inæquales & tempore & longitudine, sed quæ tamen, velut ex sole apparent æquales.
Ut EPI qua constituitur ab EBI est quidem 180 Graduum, sed apparet angulo EAI minore, quam 180 Graduum. At MPN segmentum maius absectum linea MAN & MRN segmentum minus, utrumque apparet æquale quantitate 180 Graduum.

II. De Libratione.

Doce metiri & computare librationes, & determinare intervalla?
Sit PK arcus Eccentrici minor quadrante verbi causa Gr. 46 18 pr 51 sec euius ergo complementum KD erit Gr. 43.41 pr. 9 sec euiusque sinus BL 69070 & sit Eccentricitas AB; seu dimidia libratio PH 9265 qualium BP est 100000. Multiplicatur igitur 69070 in 9265 & absectis 5 ultimis prodit libratio OH 6399 addenda ad BP vel AH in superiori semicirculo EPI eritque AO vel ei aqualia AC distantia scilicet planeta a Sole 106399 competens arcui PK vel PC qualium quidem semidiameter est 100000.
Si arcus Eccentri fuerit Gr 313 41 pr 9 sec excessus super tres Quadrantes seu 270 Gr erit etiam Gr 43 41 pr 9 sec dans sinum eundem multiplicandum: quo cum extruitur libratio 6399 ut idem addenda quippe in superiori semicirculo, sed ascendenti.
Quodsi semidiameter BP acceperit aliam dimensionem, verbi causa 152342, multiplicabimas et hanc in AC 106399 absectis 5 ultimia, et prodibit AC in hac dimensione 162090.
Artificio Neperiano conficitur tota hæc operatio expeditissime per unicam additionem. Nam sinus arcus KD logarithmus additur logarithmus Eccentricitatu 9265 & Dimensionis proposita 152343 summa quasita ut Logarithmus, exhibit librationem 9748 addendam ad Dimensionem 152342.
Sic deinde arcus PW maior quadrante, scilicet Graduum 133 39 pr 7 sec Excessus super quadratem DW Gr 43 39 pr sec euiusque vel sinus vel logarithmus cum dictum duobus pricipiis, prodit librationem 9777 subtrahenda ab 152341 quippe in inferiori Diacentri semicirculo, ut prodeat intervallum respondens AS 142565.
Idem erit, si arcus Eccentrici habuerit gr 226 20 pr 53 sec. Nam complementum eius ad tres quadrantes erit Grad 43 30 pr 7 sec tantus in ascendenti quantus DW in descendenti semicirculo.

Recense præcipuos librationis casus?

1. Quando planeta incipit discedere ab Apside: tunc simul il ratio incipit, planeta scilicet incipit descendere versus solem: qui discessum a sole Paulo prius finiverat.
2. Quando planeta habet gradus 60 ab Apside; tunc libratio æquat semissem Excentricitatis.
3. Quando planeta quadrantem orbitæ confecit ab Apsid: tunc librationis dimidium est peractum, sic ut planeta distet a sole, semidiametro Eccentrici. Ut si PD est 90 tunc AE aquat BD.
4. Quando planeta confecit gradus 120 ab Apside: tres quadrantes librationis sunt peracti.
5. Quando planeta est in ima Apside: tunc proximus soli factus, totam librationem absoluit. Contrarium est ordo per semissem Ascendentem.
6. Binæ quæque distantiæ a sole, planeta æqualibus Eccentri arcubus, ille ab Aphelio, hic a Perihelio remote, junctæ æquant Diametrum. Ut si ex C ducatur recta par B in Q, CA et AQ iunctæ æquant RP.

III. De mora Planetæ in arcu quodlibet.

Quid sonat vox Anomalia?
Et si proprie Anomalia (inæqualitas) est affection motus Planetæ: astronomi tamen sumunt hanc vocem pro motu ipso, cui inest hæc inæqualitas. Cumque ad motum hæc tria mensurabilia concurrant, spacium traiiciendum, mora temporis in spatio, & apparens magnitude spatii: vox Anomalia omnibus tribus est accomodanda. Et causa quidem temporis, rursum duplex usus est vocis. Nam primo, Ptolemæus ea utitur pro tempore toto, quod planeta consumit interim, dum restituitur omnis eius inæqualitas ad suum principium: totidem numeras Anomalias, quoties hoc fit.
Secundo, partes huius temporis totius, vulgariter Anomaliæ dicuntur. Pro eo, quod Ptolemæus dixit motum Anomaliæ, subintellige, integræ partem confictam.

Quot sunt igitur Anomaliæ sumtæ ut pars totius?
Tres nuncupantur Anomaliæ in uno quodlibet situ planetæ: 1. Anomalia media. 2. Anomalia Eccentri, & 3. Anomalia coæquata.

Quid est Anomalia Media?
Est spacium temporis, quod planeta consumit in quolibet arcusæ orbitæ, ab apside incepto, redictum in partes & minuta, qualium anomalia tota valet Gr. 360 numerationis logisticæ vel Astronomicæ.
Sie ist der Zeitraum, die der Planet für beliebige Umlaufbögen ab dem Apsisdurchgang benötigt, ausgedrückt in Teilen und Minuten, wobei die gesamte Anomalie 360 gr. misst, logisch (aufsteigend?) gezählt bzw. astronomisch.

Unde dicitur media?
Non ab eo, quasi sit quantitate media inter socias, ut paulo post cavebitur sed media dicitur imitationique veteris astronomiæ, quæ Anomaliam mediam nuncupare solet pro motu Anomaliam medio, id est, æquabili: quia tempus sic redactum in denominationem logisticam, indicat cum suo graduum & scrupulorum numero, quantum arcum circuli planeta confecturus fuisset, si toto isto tempore, quod dicimus Anomaliam mediam, incessisset motu æquabili & medio inter tardissimum & velocissimum.

Quomodo definienda vel mensuranda esset Anomalia media in his schematibus, secundum astronomiam veterem?
Constituta linea BL quæ sit ipsi AB Eccentricitati æqualis, in linea Apsidum MP ut prima huius V libri parte dictum: Anomalia media, more veteris a astronomiæ esset arcus circuli æquantis es L descripti in signorum consequentia, comprehensus inter duas lineas es L aletram per Apsidem P reliquam per corpus planetæ C traductas. Vel effectillarum linearum angulus ad L eiusqe complementum ad 4 rectos. Ut hic si C esset planeta, PLC angulus esse posset loco anomalis media fere.

Defini lineam medii motus, & locum medium planeta, secundum hanc veterem æquantis Hypothesin.
Esset linea ex centro solis in sphæram fixatum educta, parallela lineæ, quæ ex centro Aequantis, seu ex altero foco Ellipsis, per corpus Planetæ ducta est: & haberum utravis sub fixis monstraret locum planetæ medium. In schemate si C Planeta, & AM parallela ipsi LC AM esset linea motus eius medii.

Si ergo in hac astronomia forma nova nullus exprimitur circulus Aequans, qua igitur in alia quantitate numerabitur, seu mensurabitur Anomalia media?
In area comprehensa inter arcum circuli qui denominat & determinat arcum orbitæ propositum, & inter duas rectas, quæ terminus arcus cum centro solis connectuat. Ut si propositus sit locus planetæ C, ducta ex C ipsi PR perpendiculari, quæ secet circulum PD in K, & connexis P, K cum A area PKA est mensura anomalia media, qualium area totius circuli valet gr 360.

Doce computare Anomaliam mediam, seu temporis moram, quam planeta consumit in arcu proposito?
Sit rursum AB Eccentricitas 9265 qualium semidiametre BP est 100000. Ante Omnia quærenda est area trianguli maximi, quod habet angulum ab B rectum, altitudinem BD multipla hac in ipsius AB dimidium: proditigitur 463250000 Huius areæ DBA valor est experimendus numero secundorum scrupulorum, qualium at ea tota circuli PDT est Partium Grad 360 vel primorum 21600 vel secundorum 1296000. Quia igitur existente BP 100000 area circuli a Geometris proditur 31415926536 fiet area DAB 19110 secundorum.
Detur jam arcus PC per denominatorem suum PK qui sit Gr 46 18 pr. 51. Sinus igitur ipsius PK scilicet KL altitude trianguli BKA multiplicatus in valorem trianguli maximi, resectis in sine a facto quinque figuris, conficiet valorem trianguli AKB 3819 secunda, qua sunt Gr 3.50 pr 19 sec. Et vero sector KBP valet gradus totidem, quot dati sunt in arcu PK scilicet Grad 46 18 pr 51 sec additus igitur areis fit PKA Gr 50 9 pr 0 sec tanta est Anomalia Media.
Hoc pacto addenda est area Trianguli æquatorii, quam diu sector vel arcus est minor semicirculo: qui si superset semicirculum, subtrahenda est illa.

Dic regulam de affection horum Triangulorum inter se?
Bina quæque triangula, æqualiter remota verticibus, alerum a summa Apside, alterum ab ima magnitudine sunt æquali. Ut si arcus PK & RW equales area BKA BWA erunt etiam equales.

Quid est Anomalia Eccentri?
Est arcus circuli Eccentrici in consequentia numeratus: interceptusque inter lineam Apsidum & inter perpendicularem illi, per corpus planetæ, sive per punctum quodcunque Orbite propositum eductam. Ut proposito puncto orbita C aut planeta in illo versante, si per C ducatur in PAR perpendicularis KCL, secans circulum in K, PK arcus erit Anomalia Eccentri.

Quo sensu dicitur Anomalia Eccentri?
Subintelligitur & hic vocula Motus. Nam etsi in arcu ipso circuli PK secundum figuram, nulla apparet inæqualitas vel Anomalia: motus tamen planetæ in Orbita PC vere est Anomalos inæqualis, tribus nominibus, primo ratione suæ figuræ Ellipticæ, que secundum diversas sui partes flectitur inæquali curvitate, distatque a centro figuræ inæqualiter: deinde ratione celeritatis quæ non est eadem in omnibus orbitæ particulis: tertio ratione apparentiæ tanquam ex sole, quia partes Orbitæ æquales subtendunt apud solem angulos inæquales. Cum igitur arcus PK ad Omnia ista determinanda concurrat, ut prius dictum: quare quo iure verus Astronomia circulum Aequantes introduxit: inque eo numeravit Anomaliam mediam: non deteriori iure nos orbitæ reali PC circumscribimus circulum Eccentricum PK inque eo numeramus Anomalia Eccentri, usurpantes æquabile aliquid, ad mensurandum id quod est inæquabile.
Et in vereti quidem Astronomia circulus æquans seduxit physicos, ut imaginarentur sibi realem vel circulum vel certe motum: ad hic seduci nemo potest, cum appareat ad oculum, veram planetæ orbitam PC in solis duobus Apsidum punctis P, R cum hoc technico circulo PK concurrere; toto reliquo tractus est intra illius complexum versus centrum figuræ recipere.

Quid est Anomalia coequata?
Est arcus circuli magni in latitudine zodiaci per continuationem plani orbitæ planetariæ designati, in consequentia signorum numeratus a loco apsidis usque ad locum ipsum planetæ vel cujuscunque puncti orbitæ apparentem; vel, quod eodem redit, est angulus, quem arcus quilibet veræ orbitæ planetariæ subtendit aut dictæ duæ lineæ formant apud centrum Solis, ejusve anguli complementum ad 4 rectos.
Ut si planeta in C, coæquata anomalia est angulus PAC; et si planeta in Q, tunc anomalia coæquata constat his partibus: PAM, MAR duobus rectis, et insuper angulo RAQ. Quodsi centro A scribatur circulus quantuscunque, et sic etiam circulus sphæra fixarum, circuli hujus arcus, numeratus ab AP in signorum consequentiam usque ad AC vel AQ continuatas, dicetur etiam anomalia coæquata.

Quare coequata dicitur?
Motum anomaliæ coæquatum (vel simpliciter anomaliam coæquatam) dicere consueverunt auctores, non quasi ex proposito motu inæquali fuerit elicitus motus æqualis, sed ratione plane contraria, quod, cum proponatur initio tempus seu portio temporis periodici et cum hoc tempus (redactum in denominationem astronomicam) indicet, quantum arcum circuli planeta, ai incessisset motu æquabili, fuerit confecturus intra hoe temporis spatium, jam porro munus sit astronomi ostendere, quantum de motu planetæ vere inæquali apparenti respondeat huic tempori fictoque motui æquabili. Sonat igitur motue coæquatus idem, quod motus æquatione . affectus et conversus in apparentem, indutus scilicet illam inæqualitatem, quam ei conciliat apparentia, a qua inæqualitate tota periodus anomalia dicitur.

Cum igitur Anomalias hasce tres & distinxeris & formaveris per fictitium circulum Eccentricum orbita circumscriptum: quaro an non possit eidem usui esse vera planeta orbita?
Etsi non est opus , potest tamen per æquipollentiam. Nam ut prima hujus V. libri parte dictum, tempus et sic anomaliam mediam metitur etiam area PCA, et anomaliam eccentri polest, qui vult, intelligere etiam per arcum PC. Angulus vero PAC etiam prius dictus fuit anomalia coæquata.

Quomodo quantitate discernuntur tres ha sociæ Anomalia?
Numerus graduum et minutorum anomaliæ eecentri semper est medius inter ceteros. Quæ vero media dicitur, ea antequam impleat semicirculum, semper est maxima de tribus, coæquata minima; post semicirculum vero media dicta est quantitate minima, coæquata maxima.

IV.
De Angulo ad Solem.

Doce computare Anomaliam coaquantum seu Angulum ad Solem?

Varii sunt modi, sed compendiosissimus est, qui utitur intervallo planetæ & solis. Nam illo etiam ad alios usus indigemus.

Sunt autem huius modi casus tres: aut enim est planeta supra Diacentron, aut infra Dihelion, aut inter diacentron & Dihelios.

1. Sit igitur initio planeta supra Diacentron DBT
   puta in C. & Anomalia Eccentri PK Gr. 47.42.pr.20 sec. & sit per eius complementi KD sinum LB 67.277. investigate planeta libratio 6233 eaque addita ad BF. sit constitutum AC. intervallum planeta & Solis instaque 106233, in dimensione qualium BP. est 100000 in latus igitur LB. sinus complementi apponatur ad BA. eccentricitatem 9265. ut habeatur trianguli CAL. rectanguli latus alterum LA. 76542. Divisa igitur LA appositius 5. Cypheris, per CA. quotiens 72051. ut sinus, ostendit arcum Gr. 46.5 pr. 48 sec. qui est angulus LCA. cuius complementum Gr. 43.54.pr.12.sec est angulus quesitus LAC. vol PAC.
   Si Logarithmum dimidiate divisoris abstuleris a logarithmo dimidiate dividendi, relinquitur logarithmus eiusdem sive sinus, sive arcus.
2. Sit secuno planeta infra Dihelios MAN.
   puta in S & Anomalia Eccentri PW eiusque excessus supra quadrantem DW. Quem ad modum igitur supra, libratio per BZ sinum illius arcus quasita fuit a radio subtrahenda, ut existeret intervallum iustum AS sit etiam Eccentricitus BA subtrahenda nunc est a BZ sinu, veralinquatur AZ latus trianguli rectanguli alterum. Rusum igitur division numero lateris AZ per 5. cyphrus prolongato, per latus AS prodit sinus anguli ASZ cui æqualis est MAS excessus ipsius quasiti PAS super rectum PAM seu quadrantum.
3. Sit tertio planeta inter DBT & MAN ut si sit anomalis Eccentri PX eiusque excessus supra quadrantum DX sinus BY quo libratio quidem subtractoria computatur, cum sit tensus infra B at cum ipso sit minor Eccentricitate BA ipso iam ab hac aufrerendus est ut restet YA. Cum hoc igitur & cum intervallo insto agendum, ut in primo casu.

Quid appelus locum Planeta Eccentricum?

Punctum illud in Zodiaco, in quod incidis recta ex centro folis per corpus planetæ educta.

Quid est Æquatio vel Prosthaphæresis, & qua causa nominus?

XXX differentia numeri Graduum & minutorum nemalle mediæ, a Gradibus & minutis anomaliæ coæquatiæ. Vel, secundum Astronomiæ formam veceretus est angulus in centro solis, eiusque mensura, arcus circuli magni sub fixis, interceptus inter lineas medii & lineas eccentrici motus planetæ. Hic cum sit auferendus in uno semicirculo, addendus in altero ad mediuam, ut fiat coæquata: ex eo composite voce xxxxx est dicta: Æquatio vero inde: quia eius additione vel subtractione ex Anomalia coæquanta, quæ inæquales forcitur arcus & tempora in positiones æquales, sit Anomalia media æqualibilis.

Quod appellus nomen vel titulum æquationis?

Duo vocabula, vel eorum indices syllabas vel literas A.Add.S.Subt.

Quot sunt partes æquationis & quatminusque mensura?

Duæ sunt partes altera physica, altera Optica dictæ: Illa eaim est ob inæqualitatem quæ vere planetario motui accidit ob causas physicas: hæc vero ob inæqualitatem tantum modo apparentem vel quasi apparentem, hoc est, propter maiorem vel minorem remotionem arcus veræ orbitæ a sole. Utraq quodam modo in codem triangulo discernitur, quod hinc æquatorium dicitur.

Connexis enim serminis eccentricitatis AB tam corpore planeta C pars æquationis physica quidem mensuram invenit in area BAC (vel per aquipollentium, in area BAK) optica vero pars æquationis æqualis esset angulo BCA si is computaretur: quo semper exiguo minor est angulus BKA cuius esset facilior computatis.

Quis est usus huius æquationis, etiam titulorum eius?

In hac Astronomiæ forma renovate, totius æquationis ex utroque elemento compositæ usus est non necessaries nec valde magnus. Non enim per hanc æquationem, constituuntur Anomaliæ: sed ontra per comparationem anomaliæ coæquatæ: (quam prius computamus) cum Anomalia media, elicimus æquationem, si quando ea volumes uti.

In tabulis vero ponuntus tres Anomaliæ distinctæ primo enim Anomalia eccentric ponitur ad sinistram, secundum gradus integros ab 1 ad 180 ordine: idque propterea, quia ab hac data sit initium computandi reliquas, ipsamque etiam Distantiam seu intervallum planetæ & solis: secundo huic anomaliæ Eccentri subiicitur in eadem columnas pars æquationis physica seu valor areæ trianguli æquatorii in gradibus minutis & secundis: ex qua conclusione Anomaliæ Eccentri cum parto æquationis physica in eadem cellulam, intelligimus, additas in vicem constituere Anomaliam mediam respondentem. Tertio adlatus huius in peculiari columnas ponitur Anomalia coæquata, respondens arcui. Si quis iam vult scire æquationem compositam, is Anomaliam coæquata a iuxta posita media, seu a summa Anomaliæ Eccentri & parties æquationis physicæ subtrahat: remanebitque æquatio quæsitæ, quæ in semicirculo quidem descendente habet titulum Subtractoriæ, in ascendente, Adiectoriæ.

Dic tamen quomodo partes ha æquationis inter se mutue comparata, se habeant ad invictum?

Quo minor est Eccentricitas, hoc magnis accedunt ad æqualitatem inter se: in superiori tamen semicirculo, supra diacentron, Paulo minor est pars optica, parte physica, in inferiore infra diacentron, paulo maior.

Ut in adiecto schemate, si A.Sol, PAR linea Apsidum, ei, ad rectos DBT MAN superior semicirculus vel quasi DPT inferior DRT Sint Triagula aquateria in superiori BCA BFA in inferiori BSA BQA. Cuius igitur area triangulorum sint mensura parties æquationis physica, anguli vero ad CFSQ parties optica: area certe superiors sunt de area totius circui 360 portiones maiores inferiores vero minores quam earum anguli de quatuor rectis seu 360. Centris enim CS diastmatibus CB SB semidiametris, scribantur arcus BL BH terminate in CA & SA continuatam qui arcus metientur angulos C & S aque valent vero iisdem arcubus & area CBL SBH. Sic igitur ha area essent partes aquationum optica, aquales essent amba varius æquationis partes. At non CBL sed maior area CBA est mensura parties optica, sic non SBH, sed minor area SBA in inferiori Superat igitur pars physica superius, pars optica inferius.

Ubi est equation composita maxima?

Partium quidem prior, physica, est maxima in DT terminis Diacentri quia nullius trianguli altitude maior esse potast ipsa BD vel BT qui est in circula semidiametris etiamque in Ellipsi longissima ordinatium applicatorum. Posterior pars optica, si orbita circulus esset, maxima fioretim MN terminis Diheliæ: ibi onim perpendiculis ex B centro, ducta in vectorem per A esset longissima, est vero illa sinus anguli BMA parties optica qualium BM est sinus serus. Nam in EA superiorem, iam cadis ex B brevior perpendicularis quam est BA.

Seu quia Orbita planetæ est elliptica maxima igitur pars æquationis opticæ est inter M & D sic inter N & T Primum enim ipso angulus BMA maior est angulo ADE quia triangulum utrumque est rectangulum, basi eadem & vero DB altitude maior est altitude MA brevior scilicet diameter, quacumque ordinatim applicata. Deinde factis BI signis in medio arcuum DM & TN vel circiteri anguli xxx.AIB sunt iterum maiores ipsi AMB.ANE.

Xxxxxxxx ex centro B in orbitam brevissima BD ceteria xxxx, hoc longiores, longior igitur BM quam XE sensibiliter: at non sensibiliter longior perpendicularis ex B in AM quam qua ex BE in AE. Maior igitur est proportion MB ad BA quam EB ad perpendicularem suam. Itaque maior etiam angulus BEA quam BMA. Ergo bisecta BA in G ductaque perpendiculari EGI erit maxima optica aquatio circa EI. Sed maxima physica fuit circa DT maxima igitur composite cades medio loco inter DE & TI.

Docuisti computare ex proposita anomalia Eccentri, Anomaliam mediam & Anomaliam coaquantam: at crebrior usus exigis, dat a media, quipped ex dato tempore, invenire reliquas: doce & hoc?

Hic via directa nulla est: sed adhibenda est ei, qui sine tabulis hoc vult computare, regula Positionem: ponendo scilicet Anomaliam Eccentri (in schemate antepenultimo) PK tantam vel tantam, eique sic sumptæ computando suam Anomalia mediam PKA. Nam si ea tanta prodit, quanta proposita fuit, bene erit posita Anomalia Eccenta PK. At si non tanta prodit: ex eo quod prodit, emenda erit position, laborque repetendus.

Posses exemplo docere Methodum commodum, ne inassuetus nimium erret vagis propositionibus.

Resumatur igitur superius excemplu & sit iam dicta anomalia media. Seu area PKA.Gr. 50.9 pr. 10 sec manifestum est, si sciretur area trianguli KBA residuam aream KBP habituram eundem numerum graduum cum arcu suo PK ac proinde ablato valore ipsius KBA a PKA relectum iri Anomalia Eccentri PK Cum igitur PKA maior suic qua PKB erit arcus PX sinus minor: quam sinus GR. 50.9pr.10.dec. minor igitur quam 76775. Sit hic sinus in prima positione 70000 propter facilitate multiplicationis. Ductus igitur hic in valorem DBA trianguli, qui fuit in superiori exemplo 11910 sec abiectus 5 creat BKA 8337 sec seu Gr. 2.18 pr. 57 sec. qua adde ad sinus 70000 arcum Gr. 44.25 fiet area PKA Gr. 46.44 pr. Hac nimio parva est, deficit enim per Gr. 2.25 pr. Cum debuerit prodire Grad 50.9 pr. quanta est data. Maior igitur ponatus sinus in positione secundo addito defectus Grad 3.25 pr. ad arcum prius positum 44.25 ut fiat PC circiter Grad 47.50 pr. cuius sinus est proxime 74000 quem rursus eligo propter facilitate calculi. Hic in 11910 multiplicatus facit BKA iam per 7 pr 56 sec auctius, scilicet Gr. 2.26 53 sec quod adde ad PK secundo positum, scilicet ad PKB Gr. 47.44 6 sec creatur PKA Gr. 50.10 pr 59 sec & abundamus supra debitum Grad 50.9 pr. 10 sec per 1 pr 49 sec. Itaque intelligimus hunc excessum parvulum auferendum a secunda positione ipsius PK fietque Anomalia Eccentri quasita, seu PK gr. 47.42 pr. 17 sec. Id licet coprobare. Est enim sinus huius arcus 71969 qui de 11910 sec vindicate Gr. 2.26 pr 50 secun pro KBA itaque hoc addito creatur Gr. 50.9 pr 7 sec quod insensibili abest a debito Gr. 50.9 pr 10 sec.

De deflexione planetarum ab ecliptica.

Quid igitur intelligitur sub nomine orbitæ?
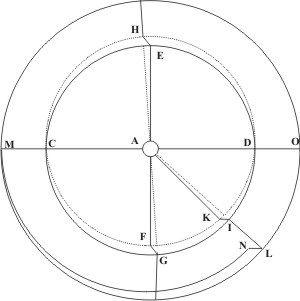
Proprie quidem illa linea, quam planeta vere circa Solem describit centro sui corporis. Ut in schemate si ECGD sit pars plani eclipticæ, HCFD erit orbita. Secundario vero intelligitur etiam circulus ille maximus, quo planum orbitæ continuatum secat sphæram fixarum. Ut hic MN sectio, tacta a plano GAK continuato.

Quid appellas inclinationem planetas vel cujusque puncti in orbita ejus, et. quid circulum inclinationis?
Inclinatio proprie competit non planetis vel punctis, sed lineis vel planis inter se; at quia plana illa circumscribuntur orbitia planetarum et quia in planis lineæ motus planetarum intelliguntur descriptæ, usu receptum est, ut hac voces simpliciter ad planetas ipsos transferantur, causa brevitatis in loquendo.
Cum igitur id, quod infra libro VI. latitudo dicetur, participet etiam de adventitia seu optica inæqualitate, quam secundam indigetamus, quare, ut res diversæ nominibus etiam distinguantur, evagatio planetæ vera ab ecliptica dicatur non latitudo, sed inclinatio; definitur autem sic, quod sit arcus circuli in fixarum sphæra maximi, ex centro Solis descripti 1 ad eclipticam recti, qui circulus inclinationis dicatur, interceptus inter eclipticam et locum planetæ eccentricum. Vel est angulus ad Solem, quem hic arcus metitur.
In schemate si A Sol, FKDHC orbita, MLO ecliptica, puncti K inclinatio erit angulus KAI vel NAL, vel ejus arcus NL ex A Sole descriptus.

Quid appellas nodos, quid limites?
Nodi sunt duo puncta eclipticæ, in quibus illa secatur ab orbitæ continuatæ plano. Græce συνδεσμοι, quod iis itinera diversa, Solis apparens et planetæ, connexa sint; ascendens alter, in quo planeta deserto hemisphærio australi deflectit in boream, alter descendeus, qui planetam in austrum transponit; vocibus ascendens et descendens ad nostrum hemisphærium accommodatis, ut in quo primi vixerunt inventores astronomiæ. Ut si planum orbitæ et planum eclipticæ concurrant linea CAD, sectionem monstrante, continuata illa sub eclipticam monstrabit M, O nodos.
Limites vero appellantur puncta eclipticæ, quæ quadrantibus a nodis distant; boreus, a quo planeta distat in boream, austrinus, a quo in austrum. Dicuntur limites ex eo, quia planeta, deveniens ad illa puncta, non evagetur ulterius in plagas, sed inde sese convertens incipiat ad eclipticam reverti. Ut in schemate E, G puncta eclipticæ dicuntur limites. Sed et H, F puncta veræ orbitæ, et puncta iis superstantia in sphæra fixarum 1 veniunt eodem nomine et hoc crebrius.

Quid appella argumentum inclinationis?
Est arcus orbitæ planetæ sub fixis, interceptus inter nodum ascendentem et locum eccentricum planetæ, numeratus in consequentia. Ut si 0 nodus ascendens N locus planetæ eccentricus, OMN erit argumentum inclinationis LN. Copernicus pro nodo ascendente sumit limitem boreum.

Num eadem est omnibus seculis inclinatio maxima limitis in quovis planeta?
Secundum principia physica libro IV. usurpata per se quidem immutabilis est, at propter ipsius eclipticæ luxationem, de qua libro VII, per accidens potest mutari.

Quomodo computatur inclinatio planetæ?
Non aliter, quam libro III. declinatio puncti eclipticæ, multiplicato sinu inclinationis maximæ in sinum argumenti inclinationis et a facto resectis 5 ultimis, apparet sinus inclinationis. Vide processum fol. 230. et seqq. Si pro sinibus arcuum utaris eorum logarithmis, multiplicatio convertetur in simplicem additionem.

Quid est locus planetæ eccentricus in ecliptica?
Punctum illud eclipticæ, in quo secatur illa a circulo inclinationis, per locum eccentricum simpliciter dictum traducto. Ut si planeta in K, locus ejus eccentricus (sic simpliciter dictus) sit N et NL circulus inclinationis, angulis NLM, NLO rectis, erit L locus planetæ eccentricus in ecliptica. Non dicitur locus eclipticus simpliciter, quia hic involvit etiam inæqualitatem secundam, libri VI. materiam; sed additur vox eccentricus, ut intelligamus, de illo . loco agi, qui determinatur sub ecliptica per solum eccentricum, remoto jam concursu orbis magni, de quo libro VI.

Quæ censetur planetæ longitudo eccentrica?
Arcus eclipticæ in consequentia numeratus a principio Arietis usque ad circulum inclinationis planetæ, seu locum eccentricum in ecliptica. Dicitur eccentrica, non quod nomeretur in eccentrico, sed quia eccentricus causatur illam.

Quæ dicitur reductio ad eclipticam?
Arena parvus, quo differunt inter se bini arcus, alter orbitæ, alter eclipticæ, a communi nodo incepti et ad circulum inclinationis terminati. Ut hic differentia inter MN et ML.

Quomodo computatur?
Non aliter quam libro III. fol. 234 ss. differentia ascensionis rectæ et arcus eclipticæ respondentis. Multiplicatur sinus complementi inclinationis maximæ in tangentem argumenti inclinationis, et absectis a facto 5. postremis, apparet tangens argumenti reducti. Vel inclinationis maximæ antilogarithmus additur mesologarithmo argumenti acervaturque hoc modo mesologarithmus arg. reducti.
Compendium utilius, etiam pro ascensione, sit hoc. Maxima reductio circa gradum 45 a nodo ducta in sinum arcus cujusque duplicati, absectis 5 ultimis, constituit reductionem arcui proposito simplo debitam.

Quomodo utendum hac reductione et ad quid?
Quando planeta pergit a nodis ad limites, auferenda est reductio ab inclinationis argumento, addenda, cum a limitibus ad nodos; quodque hoc pacto conficitur, additum loco nodi ascendentis constituit longitudinem loci planetæ eccentricam.

Quid appellas curtationem?
Est portiuncula distantiæ planetæ a centro Solis, respondens sagittæ inclinationis planetæ, in ea proportione, in qua totum intervallum respondet sinui toto. 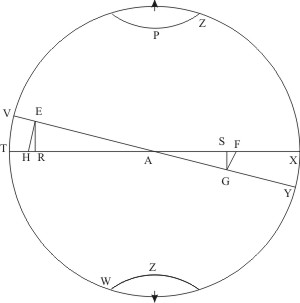Sit A Sol, P, Q poli eclipticæ, TAX repræsentet planum eclipticæ, EAG planum orbitæ; sit planeta jam in E vel G, et centro A intervallis AE, AG scribantur arcus HE, GF, et ex E, G demittantur perpendiculares in TX, quæ sint ER, GS, erunt HR et SF curationes.

Quid est distantia curtata?
Est recta in plano eclipticæ inter centrum Solis et perpendicularem ex centro corporis planetæ. In hoc schemate, planeta in E vel G versante, est AR vel AS distantia curtata.

Quomodo computatur distantia curtata?
Distantia proposita, expressa numeris dimensionis cuique planetæ propriæ, multiplicatur in sinum complementi inclinationis distantiæ propositæ competentis, et abjiciuntur a facto 5 postremæ. Seu logarithmus distantiæ additur antilogarithmis inclinationis competentis et fit logarithmus curtatæ distantiæ index.

Ubi plurimum curtatur distantia?
Circa limites et plus circa illum, qui vicinior est aphelio. Ut si V, Y eint limites, itaque Z, W poli orbitæ, et V vicinior aphelio quam Y, erit HR longior quam FS et longissima omnium.

De motu apsidum et nodorum.

Quomodo definis motum apsidis in planetis primariis?
Est arcus orbitæ sub fixis, interceptus inter id ejus punctum, quod eum certo eclipticæ puncto (puta cum principio Arietis vel etiam cum prima stella Arietis) æqualiter a nodo evehente distat, et inter locum summæ apsidis, numeratus in consequentia signorum.

Qualis est iste motus apsidis?
Statuitur æquabilis 1) propter inexspectabilem tarditatem, qua impediuntur astronomi, ut motum honc per partes singulas exactius considerare non possint, 2) quia habemus exemplum æqualitatis in uno, in quo brevis est apsidis periodus, scilicet in Luna. Itaque principia hujus motus physica, quæ libro IV. fol. 382. delibavimus, ut meris innixa conjecturis, nihil huic æquabilitati præjudicare possunt, quamvis per ea motus iste videatur inæquabilis effici posse. Sed de hoc plura lib. VI. penes planetas singulos.

Quid intelligendum ut per motum nodorum in primariis, seu quid ut nodi longitudo?
Motus nodi est arcus eclipticæ, numeratus in antecedentia signorum a certo ejus puncto (puta vel a principio Arietis, vel a loco primæ stellæ Arietis) usque ad locum nodi ascendentis. Quodsi fiat numeratio in consequentia, tunc arcus hic etiam longitudo nodi dici potest.

Qualis est hic nodorum motus?
Etsi rationabile est, etiam hujus puncti, motum in se ipso æquabilem esse, videtur ei tamen inæqualitas inesse nonnulla ex accidenti, propter luxationern eclipticæ, de qua lib. VII.

Quas figuras describunt nodi et limites motibus suis?
Nodi quidem sub circuli magno eclipticæ incedunt, limites vero orbitæ, in quantum eorum inclinatio permanere ponitur immutabilis, incedunt in circulis parallelis eclipticæ, vel ei circulo, respectu cujus inclinatio, est immutabilis.
Ad captum juvandum potest eorum motus imaginatione non inepta polorum proponi, dummodo teneamus hoc, physice loquendo polis haud opus esse. Ut in schemate proximo sit orbita VY (continuatione plani transposita sub fixas), ejus poli Z, W moveantur in parvis circellis circa eclipticæ TX poloa P, Q. In quam igitur plagam Z vergit a P quovis tempore, in eandem et limes V verget ab eclipticæ parte T et limes Y ab eclipticæ parte X, et ad circuitum ipsius Z in parvo circello, qui sit ipsi TX parallelus, in eandem plagam sequetur etiam limes V in parallelo septentrionali, tanto majori, quanto propior est ipsi TX, et sic Y in parallelo australi. Semper enim erunt in eodem circulo magno inclinationis puncta ista sex: poli orbitæ Z, W, xxli eclipticæ P, Q, et limites orbitæ V, Y.
Hactenus igitur de definitionibus terminorom orbitæ planetariæ eique circumscripti circuli eccentrici, quæ quia communia sunt omnibus planetis, libro hoc V. præmittenda fuerunt. Ceterum usum horom in planetis singulis trademus libro sequenti VI.

Finis libri quinti, Theoricæ Doctrinæ Secundi.

Liber V Primo Pars.