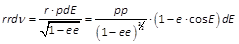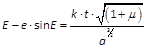Definition der mittleren Anomalie bei Kepler
Vorbemerkung
Meine Ableitung der Kepler-Gleichung hat über die Jahre immer wieder Kritik hervorgerufen, da andere Quellen die "mittlere Anomalie" als einen Winkel am Mittelpunkt der Ellipse angeben, bei mir ist es ein Winkel am Brennpunkt.
Ich habe die Gegenargumente immer zurückgewiesen mit dem Hinweis, dass keine andere Definition schlüssig auf die Kepler-Gleichung führt. Erst im Spätherbst 2011 konnte ich einen "studierten" Astronomen und bergischen Professor nicht überzeugen. Ich entschloss mich daher, in der Originalquelle nachzusehen (Keplers Werke sind inzwischen an verschiedenen Stellen im Web in digitalisierter Form einsehbar, u. a. auch bei Google Books). Leider sind die Publikationen in lateinischer Sprache geschrieben. Da erinnerte ich mich an mein Großes Latinum, und an meinen Lehrer (StR Hans Schilcher), der keine Mühe gescheut hatte, meine Lateinnote am Schuljahresende unter 5 zu drücken; er wäre sicher stolz, hätte er die Früchte seiner Mühen in meiner Kepler Übersetzung ernten können.
Ohne auf meine Mühen im Einzelnen eingehen zu wollen, ich fand im "Pars Altera" des "Liber Quintus" in Keplers "Epitomes Astronomiae Copernicanae" eine Stelle, die meine Ansicht unterstützt. (Ich habe Pars Altera übertragen und biete die transskribierte Fassung hier auf meine Website an. Weitere Teile der Übersetzung will ich im Laufe der Zeit gerne auch hier veröffentlichen.)
Keplers Anleitung zur Berechnung der mittleren Anomalie
Doce computare Anomaliam mediam, seu temporis moram, quam planeta consumit in arcu proposito?
Sit rursum AB Eccentricitas 9265 qualium semidiametre BP est 100000. Ante Omnia quaerenda est area trianguli maximi, quod habet angulum ab B rectum, altitudinem BD, multiplicata hac in ipsius AB dimidium: proditigitur 463250000. Huius areae DBA valor est exprimendus numero secundorum scrupulorum, qualium at ea tota circuli PDT est Partium Grad 360 vel primorum 21600 vel secundorum 1296000. Quia igitur existente BP 100000 area circuli a Geometris proditur 31415926536 fiet area DAB 19110 secundorum.
Detur jam arcus PC per denominatorem suum PK qui sit Gr 46 18 pr. 51 sec Sinus igitur ipsius PK scilicet KL altitudo trianguli BKA multiplicatus in valorem trianguli maximi, rejectis in fine a facto quinque figuris, conficiet valorem trianguli AKB 13819 secunda, qua sunt Gr 3.50 pr 19 sec. Et vero sector KBP valet gradus totidem, quot dati sunt in arcu PK scilicet Grad 46 18 pr 51 sec additis igitur areis fit PKA Gr 50 9 pr 10 sec tanta est Anomalia Media.
Hoc pacto addenda est area Trianguli aequatorii, quam diu sector vel arcus est minor semicirculo: qui si superset semicirculum, subtrahenda est illa.
Erkläre wie man die mittlere Anomalie berechnet, oder die Zeitverzögerung, die der Planet benötigt in dem vorgeschlagenen Bogen?
Die Exzentrizität sei wieder 9265, die Größe des Halbmessers sei 100.000. Vor allem Anderen ist zu fragen nach der Fläche des größten Dreiecks, das bei B einen rechten Winkel hat und die Höhe BD, die mit der Hälfte von AB multipliziert: ergibt 463.250.000. Dessen Fläche DBA ist die Zahl in Sekunden ausgedrückt, welchen Teil des ganzen Kreises von 360 gr. oder 21.600 (Bogen-) Minuten oder 1.296.000 (Bogen-) Sekunden. Weil also BP 100.000 beträgt, ergibt die Geometrie für die Kreisfläche 31.415.926.536 und die Fläche DAB ist 19.110 (Bogen-) Sekunden.
Gegeben ist bereits der Bogen PC durch seinen Bezeichner PK, dieser sei 46° 18’ 51". Der Sinus PK also selbst ist selbstverständlich die Höhe jenes KL im Dreieck BKA multipliziert mit dem Wert des größten Dreiecks, die letzten 5 Ziffern werden gestrichen, ergibt den Wert des Dreiecks AKB 13.819 (Bogen-) Sekunden, was 3° 50’ 19" ist. Und der Sektor KBP hat den gleichen Wert, der gegeben ist im Bogen PK selbstverständlich 46° 18’ 51" addieren der Flächen also ergibt PKA 50° 9’ 10"; so groß ist die mittlere Anomalie.
Diese Anleitung die Fläche des äquatorialen Dreiecks zu addieren, solange der Sektor oder Bogen kleiner ist als der Halbkreis: wenn er größer ist als der Halbkreis, muss man ihn abziehen.
Erläuterung der Berechnung Keplers
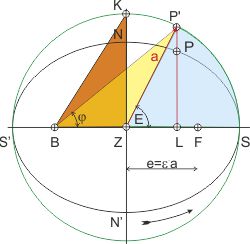
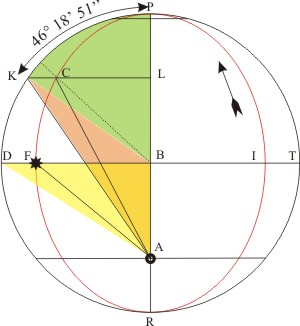 Zuerst sehen wir die vereinfachte Zeichnung aus dem Liber V Pars Altera an. (Ich habe alle Linien im Original weggelassen, die für die Argumentation hier nicht gebraucht werden.) Kepler ordnet die große Achse der Ellipse senkrecht an, mit dem Aphel P (sonnenfernster Punkt) oben und der Sonne im unteren Brennpunkt A. Der Planet befindet sich in der Nähe des oberen Brennpunktes L und ist auf der Ellipse 46° 18’ 51" weit vom Aphel entfernt. Kepler berechnet zwei Dreiecksflächen: die des triangulus maximus DBA (hier gelb) und die des Dreiecks AKB (hier rosa).
Zuerst sehen wir die vereinfachte Zeichnung aus dem Liber V Pars Altera an. (Ich habe alle Linien im Original weggelassen, die für die Argumentation hier nicht gebraucht werden.) Kepler ordnet die große Achse der Ellipse senkrecht an, mit dem Aphel P (sonnenfernster Punkt) oben und der Sonne im unteren Brennpunkt A. Der Planet befindet sich in der Nähe des oberen Brennpunktes L und ist auf der Ellipse 46° 18’ 51" weit vom Aphel entfernt. Kepler berechnet zwei Dreiecksflächen: die des triangulus maximus DBA (hier gelb) und die des Dreiecks AKB (hier rosa).
Angegeben ist der Winkel des Weges, den der Planet von Aphel P zu seinem Ort C, bzw. sein gleichförmig auf dem Umkreis bewegter Partner K, auf der Ellipse zurückgelegt hat: PC = 46° 18’ 51". Außerdem ist die Exzentizität AB gegeben.
Da Kepler noch nur mit natürlichen Zahlen rechnen durfte, setzte er den Einheitskreisradius r = 100.000 (heute gilt für den Einheitskreisradius r = 1).
Das gelbe Dreieck DBA hat die Fläche: FDBA = ½·AB·DB = ½·9.265·100.000 = 463.250.000. Um die Fläche des Dreiecks in ein Winkelmaß umzurechnen und gleichzeitig die Relation zu einem kompletten Umlauf in die Berechnung einzubringen, berechnete Kepler den Anteil des Dreiecks an der Kreisfläche. Die drückte er in Bogensekunden aus. Dazu quadrierte er den Radius r2 = 100.0002 = 10.000.000.000 und multiplizierte mit π. Das setzt er der Anzahl Bogensekunden des Kreises gleich (360°·3.600"/° = 1.296.000"). Die Fläche des Dreiecks DBA in Bogensekunden ist daher: FDBA = (463.250.000 / 31.415.926.536)·1.296.000" = 19.110".
Die Fläche des rosa Dreiecks BKA ist FBKS = ½·AB·KL. Die Strecke AB (Exzentizität) ist gegeben und KL ist durch den den Kreisbogen PK im Einheitskreis definiert: KL = sin(PK)·BP = sin(46° 18’ 51")·100.000 = 72.314. Da die Dreiecksflächen DAB und BKA ähnlich sind, und sich nur in den Höhen (DB bzw. KL) unterscheiden, kann man die Fläche FBKA durch die Multiplikation der Fläche FDBA mit dem Bruchteil von KL am Radius des Einheitskreises DB multiplizieren (Kepler multipliziert die Fläche FDBA mit KL und teilt dann durch seinen Radius des Einheitskreises (105): rejectis in fine a facto quinque figuris). Nimmt man nun die Fläche FDBA gleich in Bogensekunden, ergibt sich FBKA auch in Bogensekunden: FBKA = KL·DAB / 100.000 = 72.314·19.110" / 100.000 = 1.381.948.024" / 100.000 = 13.819" = 3° 50’ 19". (Das entspricht im Einheitskreis dem Winkel <BKA)
Nun stellt Kepler fest, dass der Winkel <KBP (hier gün) den gleichen Wert hat wie der Kreisbogen PK (Beachte: dieser Winkel hat den Scheitel am Mittelpunkt der Ellipse!). Addiert man die Fläche FBKA zu diesem Sektor, erhält man die mittlere Anomalie: <KAP = 46° 18’ 51" + 3° 50’ 19" = 50° 9’ 10" (Beachte: der Scheitel dieses Winkels ist Brennpunkt A!). Die Summe der Dreiecke (die Fläche entspricht im Einheitskreis einem Winkel!) ergibt, wie man zwanglos sehen kann, den Winkel <KAP, und das ist die mittlere Anomalie.
q.e.d. Die Mühe hat sich gelohnt! Mein Lateinlehrer kann stolz sein.
In moderner Schreibweise (mit AB = e und dem Einheitskreisradius r = 1) ist die Fläche des gelben Dreiecks DBA FDBA = ½·e·1 = ½·e. Die Einheitskreisfläche ist F = π·12 = π; sie entspricht 360°.
Und mit Keplers Argumentation ist die Fläche des rosa Dreiecks FAKB = ½·e·KL = ½·e·1·sin(PK).
Warum nun rechnet Kepler die Fläche des (rechtwinkligen) gelben Dreiecks DAB in Bogensekunden um?
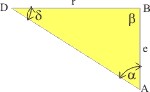 Im rechtwinkligen Dreieck DBA (der rechte Winkel ist β bei B) gilt tanα = r / e. Da r = 1, folgt: e = 1 / tanα. Eingesetzt in die Formel für die Fläche des gelben Dreiecks: FDBA = ½·e = ½·1 / tan α.
Im rechtwinkligen Dreieck DBA (der rechte Winkel ist β bei B) gilt tanα = r / e. Da r = 1, folgt: e = 1 / tanα. Eingesetzt in die Formel für die Fläche des gelben Dreiecks: FDBA = ½·e = ½·1 / tan α.
Kepler bezieht die Fläche FBKA des rosa Dreiecks BKA auf die des gelben FDBA, und zwar mit einem Faktor, der vom Winkel am Mittelpunkt, den der Planet vom Abhel zurückgelegt hat, FBKA = FDBA · sin (PK) = (1 / tanα · sin (PK).
Mathematisch gibt Kepler den Winkel α am Brennpunkt durch die Multiplikation mit der Anzahl Bogensekunden im Kreis im Bogenmaß an. Es ist der Winkel <DAP zwischen der Apsidenlinie und der Verbindungslinie vom Brennpunkt der Ellipse zum Schnittpunkt der kleinen Halbachse mit dem Umkreis.
C. F. Gauss und die mittlere Anomalie Keplers
Seit ich meine Herleitung der Kepler-Gleichung im Jahre 2003 veröffentlicht habe, wurde ich immer wieder darauf hingewiesen, dass ich den falschen Winkel als mittlere Anomalie M bezeichne. Alle anderen Quellen würden den Winkel am Mittelpunkt der Ellipse so benennen.
 Jedoch:
Jedoch:
- der Fahrstrahl Keplers 2. Gesetz geht von der Sonne aus, und die steht in einem Brennpunkt der Umlaufellipse (1. Gesetz)!
- muss also die Kepler-Gleichung eine Beziehung auf einen Winkel am Brennpunkt enthalten.
Ich habe bereits früh vermutet, dass die übliche Zuordnung des Winkels "mittlere Anomalie M" auf einem Mißverständnis von C. F. Gauss′s Ableitung beruht.
Sie findet sich in der Übersetzung von Gauss′s Werk Theoria Motus Corporum Coelestium, und wird wohl seit 1865 so abgeschrieben. Es ist mir nun gelungen, die Stelle im Ersten Buch, Ersten Abschnitt, Kapitel 6 zu identifizieren.
Der fragliche Satz im lateinischen Original lautet:
Hoc modo expressa quantitas
anomalia media vocatur, quae igitur in ratione temporis crescit, et quidem quotidie augmento
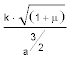 ,
,
quod motus medius diurnus dicitur. Anomaliam mediam per M denotabimus.
In der Übersetzung von Carl Hase liest sich das:
Auf diese Weise ansgedrückt heisst die Grösse
die mittlere Anomalie, die daher im Verhältnis der Zeit wächst und zwar täglich um das Augment
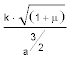 ,
,
welches man die mittlere tägliche Bewegung (motus medius diurnus) nennt. Die mittlere Anomalie bezeichnen wir durch M.
Um den Fehler zu finden, wird der lateinische Text analysiert. Dazu habe ich die lateinischen Worte des Gauss′schen Original mit ihrer Grundform und der grammatikalischen Form in der Tabelle zusammengefasst.
Verzeichnis der vorkommenden lateinischen Worte mit ihrer Übersetzung.
Der Satz lautet also in deutscher Sprache:
Die auf diese Weise
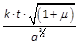 ,
,
ausgedrückte Größe wird mittlere Anomalie genannt, die im Verhältnis der Zeit zunimmt, und zwar um den täglichen Zuwachs
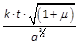 ,
,
das mittlere tägliche Bewegung genannt wird. Die mittlere Anomalie werden wir mit M bezeichnen.
Die Übersetzung ist also korrekt. Aber was meint Gauss?
Gauss stellte im Kapitel 6 seines Werkes die Differentialgleichung für die Bewegung eines Planeten um die Sonne auf, unter der Prämisse, das "die Flächenräume um die den einen Brennpunkt der Ellipse einnehmende Sonne gleichförmig sei … (s. Vorrede).
die Integration dieser Formel ergibt:
Er fährt fort:
Beide Seiten der Gleichung i) bezeichnen also Winkel, deren rechte Seite bezeichnet er als mittlere Anomalie M. Eingestzt ergibt sich:
- E - e · sin E = M
Das ist die von mir abgeleitete Kepler-Gleichung! Gauss hatte es schon richtig dargestellt, er wurde nur von irgendeinem späteren Autoren nicht richtig gelesen, und der Fehler dann immer wieder abgeschrieben.
Auch das Vorgehen zum Finden des Planetenortes auf seiner Bahn erläutert Gauss wie ich es vorführe:
- Quellen
- Johannes Kepler: Epitomes Astronomiae Copernicanae. Frankfurt 1635.
- Carolo Friderico Gauss: Theoria Motus Corporum Coelestium in Sectionibus Conicis Solem Ambientum. Hamburg 1809.
- Carl Friedrich Gauss: Theorie der Bewegung der Himmelkörper, welche in Kegelschnitten die Sonne umlaufen. Ins deutsche übertragen von Carl Haase. Hannover 1865.
- Immanuel Johannes Gerhard Schellers ausführliches und möglichst vollständiges lateinisch-deutsches Lexicon oder Wörterbuch in fünf Bänden, Leipzig 1804.
- Carl Gottlob Zumpt: Lateinische Grammatik, Berlin 1844.
- Walther Frederking: Latein ohne Umwege, BoD 2014.