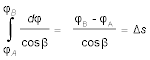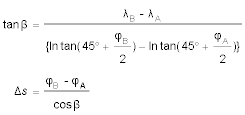Kursbestimmungen
Wenn man bei einem Törn weiss, wohin man will, bestimmt man zunächst den Kurs, mit dem man lossegeln will. Dabei unterscheidet man drei Berechnungsmethoden, die man je nach Entfernung vom Start- zum Zielort anwendet. Als nächstes interessiert bei der Törnplanung die Entfernung zwischen den beiden Orten. Die kann man aber in keinem der hier dargestellten Fälle aus der Karte ablesen: man muss immer rechnen.
- Für kurze Entfernungen, d. h. wenn man die Erdoberfläche als eben annehmen kann, verwendet man die Methode der mittleren Breite. Diese Berechnung entspricht dem Ablesen des Winkels zwischen der Nordrichtung und der Verbindungslinie der beiden Orte auf der Seekarte. Die Mercator-Projektion ist ja winkelgetreu, aber nicht flächengetreu (damit kann man Entfernungen nicht direkt aus der Karte entnehmen).
- Ist die Entfernung zu groß und muss man die Kugelgestalt der Erde berücksichtigen, rechnet man nach der Methode der Loxodrome. Die wird man anwenden, wenn Start- und Zielort nicht auf der gleichen Karte eingezeichnet sind.
- Schließlich für sehr weite Entfernungen — wenn man über mehrere Zeitzonen den kürzesten Weg sucht — verwendet man die Methode der Orthodrome.
Unter realen Bedingungen benötigt der Navigator noch ein paar Anpassungen:
- Einfluß der Strömung,
- Einfluß der Bewegung des Ziels (Treffpunktproblem),
- Besteckversetzung,
- Einfluß des Windes.
Aus den Ortskoordinaten nach der Methode der gemittelten Breite (Loxodrome)
Die auf der vorigen Seite dargestellte Berechnung der Längendifferenz in Bogenminuten in das Längenmaß Seemeilen liefert genaue Werte nur, solange die Änderung des Cosiunuswertes linear angesehen werden kann, also für kleine Breitendifferenzen. Eine genauere Methode, Bogenminuten auf Breitengraden in Seemeilen umzurechnen benutzt Kugelkoordinaten. Die verwendeten Formeln werden durch Integrieren der Differentialgleichung für die Kurslinie auf der Kugel erhalten.
Die Loxodrome schneidet alle Meridiane unter dem gleichen (Kurs-)Winkel. Wenn man sie über den Zielpunkt weiter fährt, bewegt man sich auf einer Spirale — man kommt also nicht am Startpunkt an, sondern nähert sich einem der Pole. Wenn der Winkel, unter dem die Loxodrome die Meridiane schneidet, 90° beträgt, bewegt man sich i. A. auf einem Breitenkreis (Kleinkreis, nur der Äquator ist auch ein Großkreis. Beträgt der Schnittwinkel 0°, so bewegt man sich auf einem Meridian (Großkreis).
Ableitung der Formeln für Kugelkoordinaten
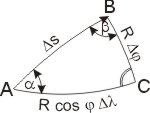
Die Erde wird in erster Näherung — und besonders für diese Berechnungen — als Kugel mit dem Radius R = 6.371 km angesehen. Die Kugelkoordinaten benutzen einen Vektor vom Erdmittelpunkt mit der Länge R des Erdradius, dessen Lage im Kugelraum durch die Längen- und Breitenwinkel angegeben wird. Man stellt sich nun vor, dass dieser Vektor von den Koordinaten des Startortes zu denen des Zielortes gedreht wird. Dabei muss der Breitenwinkel, der durchlaufen wird, der Differenz der Breitenkoordinaten und der Längenwinkel der Längendifferenz der Orte folgen. Im "ebenen" Dreieck gilt für die Entfernung (Hypotenuse) wieder die Tangensdefinition.
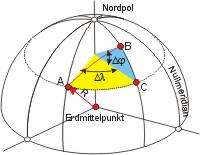 Die Länge der Strecke b entlang des Breitenkreises ist b = R · Δλ · cos φA, die Länge der Strecke a entlang des Meridians ist a = R · Δφ. (Δλ und Δφ im Bogenmaß!)
Die Länge der Strecke b entlang des Breitenkreises ist b = R · Δλ · cos φA, die Länge der Strecke a entlang des Meridians ist a = R · Δφ. (Δλ und Δφ im Bogenmaß!)
Damit ergibt sich für den Winkel β im Dreieck ABC (der Dreieckswinkel ist unabhängig von R):
In dieser Gleichung trennt man die Variablen und erhält:
Nun differenziert man diese Gleichung, d.h. man ersetzt die Änderung der Winkelkoordinaten des Vektors durch infinitesimale Änderungen.
Nun ist wegen der Beziehungen zwischen Winkelfunktionen sin x = cos (90° - x), sodass wir erhalten:
Die Integration der aufgestellten Differentialgleichung von λA bis λ B liefert also:
Die Länge der Seite c = Δs ergibt sich aus der Definition des Sinus:
Integrieren liefert die Formel für die Berechnung der Entfernung:
Wir haben nun die beiden Gleichungen für den Kurswinkel und die Entfernung zwischen zwei Orten.
Die Formeln gelten für die Kugel mit dem Radius R = 1 (Einheitskugel). Da aber die Entfernung Δs auf der Kugeloberfläche der Erde mit dem Radius R = 6.371 km berechnet werden soll, muss man den Winkel Δs als Bruchteil des Vollwinkels bzw. des Erdumfangs U (360° = 21.600´ = 2 · π · R = U) betrachten. Man rechnet in Bogenminuten, da 1´ = 1 sm. Also wird Δs durch 2 · π geteilt und mit R = 21.600´ multipliziert.
Beispielrechnung
Die Fahrt soll von Helgoland (54° 11′N, 007° 53′ E) nach Calais (50° 58′ N, 001° 51′ E) gehen. Zunächst werden die natürlichen Logarithmenterme Φ = ln tan(45° + ½·φ) der Winkelgleichung berechnet (zum Ablesen der Skalen siehe hier):
- ΦCalais = ln tan (45° + ½ · 50,96°) = ln tan 70,48° = ln 2,82 = 1,037
- ΦHelgoland = ln tan (45° + ½ · 54,18°) = ln tan 72,09° = ln 3,09 = 1,129
Diese beiden Zahlen haben keine Benennung; damit wir auf und unter dem Bruchstrich die gleichen Zahlen (Bogenminuten = Seemeilen) haben, berechnen wir die Bogenlänge in Seemeilen (Bogenminuten). Dazu multiplizieren wir mit R = 21.600 ⁄ 2π:
- ΦHelgoland - ΦCalais = 0,092 · 10.800 ⁄ π = 316′.
Die Differenz λCalais - λHelgoland geben wir ebenfalls in Bogenminuten an: -111′ + 473′ = 362′. Nun können wir auf dem Rechenschieber den Quotienten bilden und den Winkel ablesen: β = 48,88°.
Mit diesem Winkel berechnen wir nun die Entfernung Δs = 192,6′ ⁄ cos 48,88° = 292′. Die Umrechnung des Dreieckswinkels β in Kurswinkel (KaK) erfolgt nach der gleichen Überlegung wie auf der vorigen Seite.
|
|
© Rainer Stumpe URL: http://www.rainerstumpe.de |