Die Bedeutung der Sinustabellen in der Trigonometrie
Die von Hipparch wohl als erstem berechneten Sinustabellen stellen den Anfang der Trigonometrie dar. Bis in die Neuzeit wurde allerdings die Länge einer Kreissehne als "Sinus" bezeichnet, d. h. die Länge war nicht nur vom Winkel, sondern auch vom Kreisradius abhängig. Zur Nomenklatur die Abbildung aus [1]:
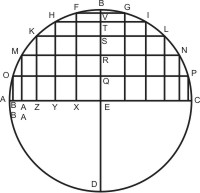
- ac est tota diameter circuli similiter linea bd.
- ae est semidiameter circuli.
- abcd est periferia sive circumferentia circuli.
- fg est chorda arcus fb.
- fv est rectus primus arcus fb.
- fx est sinus rectus secundus ipsius arcus fb.
- bv est sinus versus sive sagitta arcus fb.
- hi est chorda arcus hfbgi.
- ht est sinus arcus hb.
- hy est sinus coplementi vel sinus secundus arcus hb.
- bt est sinus versus vel sagitta arcus hb.
Als "Sinus" wird die Halbsehne HT (Sehne oder Chord ist HI) des Kreisbogens HB bezeichnet, der durch den Winkel ∢HEB am Mittelpunkt E des Kreises aus dem Umfang geschnitten wird.
Die Sehnentabelle des Hipparch ist verloren; Toomer hat versucht, die Argumentation nach zu vollziehen.
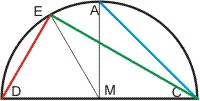 Wenn CD = d der Durchmesser eines Kreises ist, dann hat die Sehne AC eines rechten Winkels ∢AMC = 90° die Länge S(90°) = ½ · d · √2 (mit dem Satz des Pythagoras). Die Sehne DE zu einem Winkel ∢DME = 60° hat die Länge S(60°) = ½ · d (DEM ist gleichseitig). Nun ist auch die Sehne CE über dem Komplementärwinkel ∢EMC = 180° - ∢DME: DE2 + CE2 = d2 (Satz von Thales: ∢DEC = 90°).
Wenn CD = d der Durchmesser eines Kreises ist, dann hat die Sehne AC eines rechten Winkels ∢AMC = 90° die Länge S(90°) = ½ · d · √2 (mit dem Satz des Pythagoras). Die Sehne DE zu einem Winkel ∢DME = 60° hat die Länge S(60°) = ½ · d (DEM ist gleichseitig). Nun ist auch die Sehne CE über dem Komplementärwinkel ∢EMC = 180° - ∢DME: DE2 + CE2 = d2 (Satz von Thales: ∢DEC = 90°).
Mit einer ähnlichen Argumentation findet man auch eine Formel für halbe Winkel.
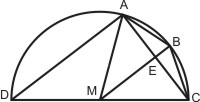 Wenn die Länge der Sehne AC zum Winkel ∢AMC bekannt ist und BM den Winkel ∢AMC halbiert, so gilt nach dem Satz von Thales für die Sehne AB = BC: BC2 = EC2 + EB2 (∢BEC = 90°!) und EC = ½ · AC (siehe Sätze über Kreis und Gerade). Und da EB = MB - ME = ½ · - ½ · AD (AD ist die Sehne des Komplementärwinkels ∢AMD zu ∢AMC). Mit diesem Formelsatz (und einiger Mühe) kann man eine Sehnentabelle mit einer Winkelschrittweite von 7½° berechnen. Mit der späteren Erkenntnis, dass die Sehne über dem halben Winkel halb so lang ist wie die über dem ganzen, konnte Aryabhata die Tabelle auf eine Schrittweite von 3¾° erweitern.
Wenn die Länge der Sehne AC zum Winkel ∢AMC bekannt ist und BM den Winkel ∢AMC halbiert, so gilt nach dem Satz von Thales für die Sehne AB = BC: BC2 = EC2 + EB2 (∢BEC = 90°!) und EC = ½ · AC (siehe Sätze über Kreis und Gerade). Und da EB = MB - ME = ½ · - ½ · AD (AD ist die Sehne des Komplementärwinkels ∢AMD zu ∢AMC). Mit diesem Formelsatz (und einiger Mühe) kann man eine Sehnentabelle mit einer Winkelschrittweite von 7½° berechnen. Mit der späteren Erkenntnis, dass die Sehne über dem halben Winkel halb so lang ist wie die über dem ganzen, konnte Aryabhata die Tabelle auf eine Schrittweite von 3¾° erweitern.
Verbesserungen machte Ptolemäus mit der Anwendung des nach ihm benannten Lehrsatzes (Im Sehnenviereck ist das Produkt der Diagonalen gleich der Summe der Ptodukte der gegenüberliegenden Seiten.).
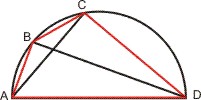
- AD · BC + AB ·CD = AC · BD
Eingesetzt in die Formel aus dem Satz des Ptolemäus ergibt
- d · (γ - α) + α · (180° - γ) = γ · (180° - α)
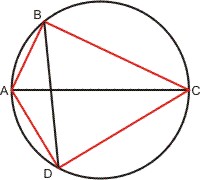
Die Gleichung enthält außer dem Kreisdurchmesser d nur noch die Kreisbögen (Winkel). Allerdings ist die Differenz γ - α nicht auflösbar. Wir brauchen also noch die Summe der Winkel γ + α. Das erreichen wir, wenn wir den Kreisdurchmesser d als eine der Diagonalen des Sehnenvierecks nehmen. Mit {AB} = AB = α, {AD} = AD = β, {BC} =BC = (180° - α), {CD} = CD = (180° - β), {BD} = BD = (α + β) und {AC} = AD = d ergibt der Satz des Ptolemäus:
- β · (180° - α) + α · (180° - β) = d · (α + β)
Nun konnte Ptolemäus auch den Bogen über einem Winkel von 36° als Seite eines dem Kreis eingeschriebenen Zehnecks berechnen, und mit den oben erläuterten Gleichungen für halbe Winkel auch die Bögen über 6°, 3°, 1½° und ¾°. Durch Interpolation erhielt er auch den Bogen über 1°.
Zur Erstellung der Sehnentafel teilte Ptolemäus den Durchmesser des Kreises in 120 Teile d = 120p und konnte so die Länge der Sehne einer Bogenlänge zuordnen. Das sieht dann so aus (Auszug):
| Winkel | Sehne |
| 36° | 37p 4′ 55″ |
| 60° | 60p 0′ 0″ |
| 72° | 70p 32′ 3″ |
| 90° | 84p 51′ 10″ |
| 108° | 97p 4′ 56″ |
| 120° | 103p 55′ 23″ |
| 144° | 114p 7′ 37″ |
| 180° | 120p 0′ 0″ |
Im Rahmen der damaligen Meßgenauigkeit auf ½° war es so möglich, seine Welttheorie durch Beobachtung zu bestätigen.
Bis auf einige Neuberechnungen nach anderen Methoden (z. B. durch Aryabhata) oder mit größerer Genauigkeit (längerer Radius ergibt mehr Stellen) haben sich die Sinustabellen nicht wesentlich weiterentwickelt. Die von Al Zarquali zusammengestellten Canones Sive Regulae Super Tabulas Toletanas waren die Grundlage der Astronomie bis in die Zeit von Regiomontanus.
 Der veröffentlichte im Eigenverlag (vermutlich 1475 in Nürnberg) die Tabula Sinus Recti: per gradus et singula minuta divisa mit einem Kreisdurchmesser von 120.000 Teilen. Die Sinus-Tabllen hat Regiomontanus bis zu einem Radius von 10.000.000 berechnet (man bedenke den Rechenaufwand!). Aber mit diesen genauen Daten konnte er die Ephemeriden der Sterne so exakt voraus berechnen, dass die Tabellen den Entdeckern zur Navigation dienten. Christopher Columbus (1492 - 1504), Vasco da Gama (1497 - 1524), Amerigo Vespucci (1497 - 1504) und wohl auch vielen anderen.
Der veröffentlichte im Eigenverlag (vermutlich 1475 in Nürnberg) die Tabula Sinus Recti: per gradus et singula minuta divisa mit einem Kreisdurchmesser von 120.000 Teilen. Die Sinus-Tabllen hat Regiomontanus bis zu einem Radius von 10.000.000 berechnet (man bedenke den Rechenaufwand!). Aber mit diesen genauen Daten konnte er die Ephemeriden der Sterne so exakt voraus berechnen, dass die Tabellen den Entdeckern zur Navigation dienten. Christopher Columbus (1492 - 1504), Vasco da Gama (1497 - 1524), Amerigo Vespucci (1497 - 1504) und wohl auch vielen anderen.
Sein Werk De triangulis omnimodus libri quinque. (1464) war eine kritisch kommentierte Zusammenfassung der damals bekannten Trigonometrie. Es wurde sehr populär in Europa und begründete seinen Ruf als herausragender Mathematiker, obwohl die Behandlung der sphärischen Trigonometrie wohl auf der — auch schon kritisch-verbesserten — des Jabir ibn Aflah beruhte.
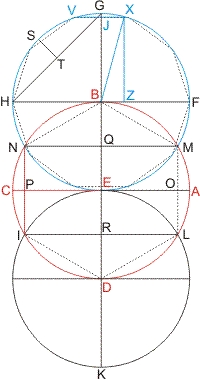 Johannes von Gmunden gibt in seinem Werk Tractatus de Sinibus, Chordis et Arcubus (1437) eine Zusammenfassung der Berechnungsmethoden auf der Basis Euclids und der Arbeiten des Al-Zarkali. Zuerst definiert er den Sinus rectus als die halbe Sehne des doppelten Bogens (abgekürzt crd) (sinus rectus α = ½ · crd 2 · α, d. i. HT), den Sinus versus (sin vers α = 1 - cos α, d. i. ST), den Sinus totus (= sin 90°, d. i. HG), und die Kardaga (= crd 15°, d. i. NP).
Johannes von Gmunden gibt in seinem Werk Tractatus de Sinibus, Chordis et Arcubus (1437) eine Zusammenfassung der Berechnungsmethoden auf der Basis Euclids und der Arbeiten des Al-Zarkali. Zuerst definiert er den Sinus rectus als die halbe Sehne des doppelten Bogens (abgekürzt crd) (sinus rectus α = ½ · crd 2 · α, d. i. HT), den Sinus versus (sin vers α = 1 - cos α, d. i. ST), den Sinus totus (= sin 90°, d. i. HG), und die Kardaga (= crd 15°, d. i. NP).
Durch Konstruktionen nach Euklid (Quadrat über einer Strecke, gleichflächiges Rechteck, u. s. W.) bestimmt er
- NP = sin 30° = ½ · CE = ½ · r.
- NQ = sin 60° = √(r2 - NP2).
- HT = sin 45° = ½ · √(2 · r2).
- ½ · AM = sin 15° = √(OM2 + OA2).
Nun argumentiert er Al-Zarkali folgend im roten Kreis mit dem eingeschriebenen Sechseck. Die Bögen über den Seiten des Sechsecks (z. B. BN) lassen sich leicht halbieren (z. B. CN) und so erhält man Bögen, die 15° entsprechen. Beginnend mit dem Punkt A:
- Sinus der 1. Kardaga: sin 15°
- Sinus der 2. Kardaga: sin 30° - sin 15°
- Sinus der 3. Kardaga: sin 45° - sin 30°
- Sinus der 4. Kardaga: sin 60° - sin 45°
- Sinus der 5. Kardaga: sin 75° - sin 60°
- Sinus der 6. Kardaga: sin 90° - sin 75°
nun behauptet er analog Al-Zarkali ohne Beweis:
- sin 15° = sin vers 90° - sin vers 75°
- sin 30° = sin vers 75° - sin vers 60° + sin vers 90° - sin vers 75°
- …
- sin vers 45° = 1 - cos 45° = sin 60° -sin 45° - sin 75° - sin 60° + sin 90° - sin 75°
Mit den Formeln sin2 α = sin 30° sin vers 2 · α und sin2 (90° - α) = 1 - sin2 α berechnet Johannes von Gmunden nun die Sinusse der Vielfachen von sin 3° 45′ und erstellt Tabellen.
Als im Jahre 1515 das Amalgest des Ptolemäus in lateinischer Sprache gedruckt in Europa verbreitet wurde, und die Messungen Ungereimtheiten offenbarten, begann die "Renaissance der Astronomie" in Europa. Regiomontanus publizierte eine Zusammenfassung (Epitoma Johanis De Monte Regio in Amalgesti Ptolomei, undatiert) und Nicolaus Copernicus reformierte das Weltbild: die Planeten bewegen sich auf Kreisbahnen um die Sonne.
Inzwischen waren auch die astronomischen Meßgeräte weiter entwickelt worden, deren gesteigerte Meßgenauigkeit auch präzisere Sinustabellen verlangten und genauere Berechnungen ermöglichten. Tycho Brahe vermaß die Planetenbahnen so genau, dass erneut Widersprüche zwischen Theorie und Beobachtung auftraten. Die löste Johannes Kepler mit dem Postulat elliptischer Planetenbahnen um die Sonne. Seine "Ephemeriden" erlaubten so genaue Vorhersagen, dass die römische Kirche ihren Widerstand gegen das heliozentrische Weltbild aufgab.
Leider stieg mit den Ellipsenbahnen auch der Rechenaufwand. Zwar hatte im Jahre 1510 Johannes Werner die "Prosthapharese" erfunden, die das Multiplizieren vielstelliger Zahlen auf die Addition von Sinuswerten aus den Sinustabellen reduzierte, aber das vermied eher Multiplikationsfehler als es schnell und bequem war.
Die Prosthaphairese
Mit diesen Sinustabellen konnte man einfach die Aufgaben im sphärischen Dreieck berechnen. Statt der umständlichen Multiplikation und Division von Sinuswerten gab es eine geniale Abkürzung: die Prosthaphairese.
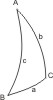 In einem rechtwinkligen sphärischen Dreieck ABC mit c = 66° 29′ und α = 23° 31′ ist die Seite b gesucht.
In einem rechtwinkligen sphärischen Dreieck ABC mit c = 66° 29′ und α = 23° 31′ ist die Seite b gesucht.
| größter Winkel | 66° 29′ | Komplement | 23° 31′ | ||
| kleinerer Winkel | 23° 31′ | 23° 31′ | |||
| Summe | 47° 2′ | Sinus (aus Tabelle) | 7.317.503 | ||
| die Hälfte | 3.658.751 | ||||
Aus der Sinustabelle findet man den zu 3.658.751 gehörigen Winkel durch Interpolation: b = 21° 27′ 41″.
Wie funktioniert das? Nach der Neperschen Regel gilt: der Cosinus eiens Stücke ist gleich dem Produkt der Cotangenten. Die beiden gegebenen (c, α) und das gesuchte Stück b sind "anliegend" in der Reihenfolge a* β c α b*. Also ist cos α = cot c · cot b* = cot c · tan b. Aus den Beziehungen der Winkelfunktionen wissen wir: tan χ = sin χ ⁄ cos χ und cot χ = cos χ ⁄ sin χ.
Aber gerechnet wird offensichtlich die Formel:
- sin b = ½ · sin (90° - c + α).
Diese Formel geht auf Johannes Werner, genannt der Nürnberger, zurück. Sie wird als erste der Formeln der Prosthaphaerese bezeichnet. Er beschreibt die Ableitung im vierten Buch seiner Abhandlung De Triangulis Sphæricis, Propositiones Prima – Quinta.
Quellen
- Petrus Apianus: Introductio Geographica, Ingolstadt 1533.
- Brian Borchers: Prosthaphaeresis. Journal of the Oughtred Society, 14(2):3-4, 2005.
- Helmut Gericke: Mathematik in Antike, Orient und Abendland. Fourier Verlag, 2003.
- Karl Manitus (Übers.): Des Clausdius Ptolemäus Handbuch der Astronomie, Teubner, Leipzig 1912.
- Glen Elert: Ptolemy's Table of Chords. 1994
- Dictionary of the History of Science. W. F. Byrum, E. J. Browne, Roy Porter (Herausg.), The Macmillan Press, London 1983.
- H. L. L. Busard: Der Traktat "De Sinibus, Chordis et Arcubus" des Johannes von Gmunden. Geschichte der Mathematik und der Naturwissenschaften, Heft 10, 73-113. Springer-Verlag Wien, 1971.
- Clavis universi trigonometrica: per quam coeli ag terrae adyta recludi. gedruckt von Georg Ludwig Frobenius, Hamburg 1634.
Biografische Notizen
- Al Zarquali
- arab. Mathematiker und Astronom. * 1029 in Toledo, † 1087 in Sevilla. Konstruierte Präzessions-Astrolabien, stellte die "Toledaner Tabellen" zusammen (in Latein von Gerard von Cremona (1114-1187) übersetzt und in Europa verbreitet).
- Aryabhata
- indischer Mathematiker und Astronom, geb. 21.03.476 in Kusumapura, gest. um 550. Gebrauchte als erster die Sinusfunktion, lehrte die Achsendrehung der Erde und löste Gleichungen durch Kettenbrüche.
- Nicolaus Copernicus
- poln.-deutscher Astronom. * 16.02.1473 in Thorn (heute Thoruń) † 24.05.1543 in Frauenburg (heute Frombork). Begründete das nach ihm benannte heliozentrische Weltbild (De revolutionibus orbium coelestium, 1543).
- Johannes von Gmunden
- österreichischer Astronom und Mathematiker. * verm. 1385, † 22.02.1442. Er gab mit seinem Werk Tractatus de Sinibus, Chordis et Arcubus (1437) den Anstoss zur Neuberechnung der überkommenen Sinustabellen.
- Hipparch von Nicäa
- griech. Astronom und Mathematiker, * um 190 v. Chr. in Nicäa, † um 120 v. Chr. auf Rhodos. Entdeckte die Präzession der Erdachse /Verschiebung der Àquinoktien), erstellte eine Tabelle der trigonometrischen Sehnen (Chorden).
- Jabir ibn Aflah
- arab. Mathematiker und Astronom. 1100 - 1150 in Sevilla. Bearbeitete Ptolemäus's Werke und führte sie weiter. Da sein Werk von Gerard von Cremona ins Lateinische übersetz worden war (Korrektur des Amalgest) beeinflusste er die abendländische Astronomie.
- Ptolemäus
- griech Astronom und Mathematiker, * um 100 n. Chr. in Àgypten, † nach 160 n. Chr. in Alexandria. Entdeckte die Präzession der Erdachse /Verschiebung der Àquinoktien), erstellte eine Tabelle der trigonometrischen Sehnen (Chorden). Entwickelte das nach ihm benannte geozentische Weltbild.
- Regiomontanus
- Johannes Müller (latinisiert: Molitoris), genannt "der Königsberger" (latinisiert: Regiomontanus; geb. 6. Jun. 1436 in Königsberg (OT Unfinden, Unterfranken), † 8. Jul 1476 in Rom. dt. Astrologe, Astronom und Mathematiker. Gab Ephemeriden heraus, die von u. a. Christopher Columbus (1492 - 1504), Vasco da Gama (1497 - 1524), Amerigo Vespucci (1497 - 1504) benutzt wurden. Das Hauptwerk De triangulis erschien posthum im Jahr 1533, war aber wohl aus Briefewechseln bekannt.
- Gerald James Toomer
- englischer Mathematik-Historiker, * 23.11.1934 in Aldershot. Arbeitete über antike griechische Mathematik, besonders die Werke von Hipparch, Ptolemäus und Apollonius.
- Johannes Werner
- Pfarrer in Nürnberg, * 14.02.1468 † 1528 ebenda. Beschäftigte sich mit Astronomie und Trigonometrie und schrieb Bücher, umfangreiche Korrespondenz mit den Größen seiner Zeit. Gilt als Erfinder der Prosthaphaerese.
|
|
© Rainer Stumpe, URL: http://www.rainerstumpe.de |