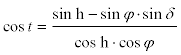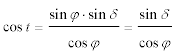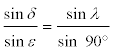Sphärische Trigonometrie
Anwendungen
Die Orthodrome
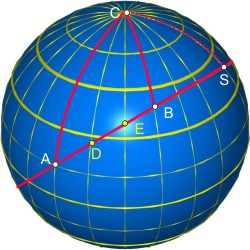
Die kürzesten Verbindungslinie zwischen zwei Punkten A und B auf der Kugel liegt auf einem Großkreis. Die Fahrt auf der Orthodrome ist also die kürzeste Route von A nach B. Dieser Großkreis — sofern er nicht der Äquator oder ein Breitenkreis ist — schneidet jeden Meridian unter einem anderen Winkel. Das hat den Nachteil, dass man ständig den Kurs wechseln muss.
Mit dem Pol bilden die beiden Punkte A unf B ein — in aller Regel schiefwinkliges — sphärisches (Pol-)Dreieck ABC, denn die Punkte A und B liegen auf Meridianen. Wenn man die Koordinaten der Punkte A und B kennt, sind die Seiten a und b bekannt und der eingeschlossene Winkel γ (das ist der Längenunterschied von A und B) gegeben, und die Seite c und die Winkel α und β sind gesucht. Das ist die Hauptaufgabe III im sphärischen Dreieck. Also kann die Seite c nach der Formel
berechnet werden. Die Winkel berechnet man analog der Hauptaufgabe I im schiefwinkligen sphärischen Dreieck:
Wenn man also von A nach B segeln will, sind der Startkurs α und der Ankunftskurs β bekannt.
Aber wie findet man die Schnittwinkel in den Punkten D und E auf der Orthodrome mit den zwichen A und B liegenden Meridiane? In den Hauptaufgaben V und VI beim schiefwinkligen sphärischen Dreieck haben wir den Trick kennen gelernt: man erzeugt aus einem schiefwinkligen Dreieck zwei rechtwinklige, indem man die sphärische Höhe h von einer Ecke aus einzeichnet. Sie hat den Fußpunkt S, und ist die Höhe in jedem beliebigen Dreieck, das C und S als zwei seiner Ecken hat, und dessen dritte Ecke auf dem Großkreis der Orthodrome liegt. Mit der Verwendung von rechtwinkligen sphärischen Dreiecken werden die Berechnungen einfacher.
Zunächst aber müssen die Koordinaten des Scheitelpunktes gefunden werden. Das ist mit der Neperschen Regel recht einfach. Im Dreieck ASC mit dem rechten Winkel bei S (∢CSA) werden die Stücke angeordnet: AS* α AC γ CS* (der Winkel ∢ACS ist γ im Dreieck ACS!). Bekannt sind AC und α, also nicht-anliegende Stücke zum gesuchten Bogen CS. Man erhält für den Komplementärwinkel der Scheitelbreite die Formel:
-
cos CS* = sin AC · sin α = sin CS = sin AC · sin α
- Und als Formel für die Scheitellänge AS:
-
cos γ = cot c · cot CS*
Die Berechnung an einem Beispiel wird im Abschnitt Navigation ausgeführt.
Die Berechnung der Tageslänge
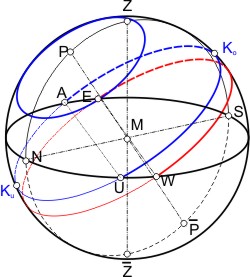
Die Sonne — und die Sterne — bewegen sich von der Erde ausgesehen auf Kreisen um einen imaginären Punkt. Die größte Höhe über dem Horizont erreicht die Sonne etwa zu Mittag (außer wenn gerade "Sommerzeit" angesagt ist). Die Tageslänge hängt von der Jahreszeit ab. In der Abbildung ist der sphärisch-trigonometrische Zusammenhang vereinfacht dargestellt (der Durchmesser der Erde ist hier vernachlässigt, d. h. der "wahre" Horizont fällt mit dem "scheinbaren" zusammen).
Der Beobachter steht im Mittelpunkt M der Himmelskugel, über ihm ist der Zenith Z und der Himmel trifft auf den Horizont, der das Gesichtsfeld begrenzt. Die Horizontebene ist ein Großkreis, der auf der Achse MZ senkrecht steht. Die Sterne bewegen sich im Verlaufe eines Tages auf Kleinkreisen (hier blau) mit den Mittelpunkten auf der Achse MP, der Weltachse. Die Großkreisebene senkrecht zur Weltachse ist der Himmelsäquator (hier rot). Der höchste Punkt der Sternenbahn vom Beobachter aus gesehen, ist der (obere) Kulminationspunkt KO, der die Südrichtung (S) definiert. "Westen" (W) ist rechts vom Beobachter, der nach Süden blickt, "Osten" (E) links, und "Norden" (N) liegt hinter ihm. Alle Sterne gehen im Osten auf (Aufgangspunkt A) und im Westen unter (Untergangspunkt U).
In der Abbildung sind zwei durch je eine Großkreisebene und ihre senkrechte Mittelachse definierte Koordinatensysteme enthalten: das Horizontsystem und das Reaktaszensionssystem. In beiden Koordinatensystemen ist jedoch die Südrichtung als Bezugspunkt in der Großkreisebene festgelegt. Damit sind die Systeme durch den Großkreis durch P und Z mit einander verbunden.
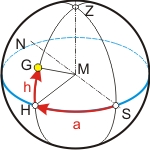 Aus historischen Gründen muß eine Nomenklatur eingeführt werden (die unterschiedlichen Bezeichnungen beziehen sich auf das jeweilige Koordinatensystem). Im Horizontsystem misst man den Winkel zwischen dem Großkreis durch den Zenith Z, auf dem der Stern G steht, und dem Meridian, der durch den Südpunkt geht, von Süd nach Westen von 0° bis 360°. (Es gibt auch andere Konventionen!) Man nennt diesen Winkel Azimuth a. Der Winkel zwischen dem Äquator und dem Stern G heißt Höhe h. Der Azimuth a gibt die Richtung an, in der die Sonne steht, gemessen vom OrtsMeridian.
Aus historischen Gründen muß eine Nomenklatur eingeführt werden (die unterschiedlichen Bezeichnungen beziehen sich auf das jeweilige Koordinatensystem). Im Horizontsystem misst man den Winkel zwischen dem Großkreis durch den Zenith Z, auf dem der Stern G steht, und dem Meridian, der durch den Südpunkt geht, von Süd nach Westen von 0° bis 360°. (Es gibt auch andere Konventionen!) Man nennt diesen Winkel Azimuth a. Der Winkel zwischen dem Äquator und dem Stern G heißt Höhe h. Der Azimuth a gibt die Richtung an, in der die Sonne steht, gemessen vom OrtsMeridian.
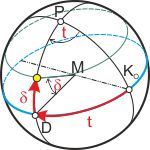 Auf den ersten Blick sieht die Abbildung rechts aus wie die oben links. Sie stellt aber ein anderes Koordinatensystem dar: das Rektaszensionssystem. Der blaue Großkreis ist hier der Himmelsäquator, die darauf senkrecht stehende Achse durchstößt die Himmelskugel im Himmelspol. Der Winkel zwischen dem Meridian, auf dem der Stern steht, und dem der oberen Kulmination des Sterns heißt hier der Stundenwinkel t oder die Rektaszension α, und der Winkel vom Äquator zum Pol heißt Deklination δ des Sterns. Im Rektaszensionssystem bewegt sich der Stern auf einem Kleinkreis parallel zum Äquator. Der Meridian der oberen Kulmination ist die Südrichtung im Horizontsystem. Der Stundenwinkel gibt die Zeit seit der Kulmination an, er kann in Grad umgerechtet werden, weil der Vollkreis mit 360° in 24 Stunden (= 1 Tag) durchlaufen wird. Ein Stundenwinkel von 1 Stunde entspricht deshalb 360° ⁄ 24 h = 15 ° ⁄ h. Da die Deklination δ eines Sterns von der irdischen Zeit — in erster Näherung — unabhängig ist, kann man für jeden Stern die Deklination, also den Abstand von der Äquatorebene, in einer Tabelle angeben. (Da gegenüber dem Durchmesser der Sonnenbahn der Erddurchmesser nicht vernachlässigbar ist, ändert sich die Deklination der Sonne täglich! Sie kann im ekliptikalen Koordinatensystem berechnet werden.)
Auf den ersten Blick sieht die Abbildung rechts aus wie die oben links. Sie stellt aber ein anderes Koordinatensystem dar: das Rektaszensionssystem. Der blaue Großkreis ist hier der Himmelsäquator, die darauf senkrecht stehende Achse durchstößt die Himmelskugel im Himmelspol. Der Winkel zwischen dem Meridian, auf dem der Stern steht, und dem der oberen Kulmination des Sterns heißt hier der Stundenwinkel t oder die Rektaszension α, und der Winkel vom Äquator zum Pol heißt Deklination δ des Sterns. Im Rektaszensionssystem bewegt sich der Stern auf einem Kleinkreis parallel zum Äquator. Der Meridian der oberen Kulmination ist die Südrichtung im Horizontsystem. Der Stundenwinkel gibt die Zeit seit der Kulmination an, er kann in Grad umgerechtet werden, weil der Vollkreis mit 360° in 24 Stunden (= 1 Tag) durchlaufen wird. Ein Stundenwinkel von 1 Stunde entspricht deshalb 360° ⁄ 24 h = 15 ° ⁄ h. Da die Deklination δ eines Sterns von der irdischen Zeit — in erster Näherung — unabhängig ist, kann man für jeden Stern die Deklination, also den Abstand von der Äquatorebene, in einer Tabelle angeben. (Da gegenüber dem Durchmesser der Sonnenbahn der Erddurchmesser nicht vernachlässigbar ist, ändert sich die Deklination der Sonne täglich! Sie kann im ekliptikalen Koordinatensystem berechnet werden.)
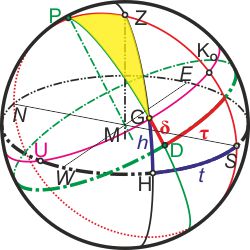 Legt man nun das Horizontsystem und das Rektaszensionssystem so übereinander, dass die Mittelpunkte zusammenfallen und der Pol P des Rektaszensionssystem (blau) auf dem Südmeridian (rot) des Horizontsytems (schwarz) liegt, erhält man die nebenstehende Abbildung. Das gelb gefüllte Dreieck PZG ist das "Navigationsdreieck"; es ermöglicht die beobachteten Höhe h des Sternenorts G in Beziehung zu setzen mit der Tageszeit t und dessen Deklination δ, denn die Seite PG liegt im Rektaszensionssystem, die Seite ZG im Horizontsystem und die Seite PZ in beiden.
Legt man nun das Horizontsystem und das Rektaszensionssystem so übereinander, dass die Mittelpunkte zusammenfallen und der Pol P des Rektaszensionssystem (blau) auf dem Südmeridian (rot) des Horizontsytems (schwarz) liegt, erhält man die nebenstehende Abbildung. Das gelb gefüllte Dreieck PZG ist das "Navigationsdreieck"; es ermöglicht die beobachteten Höhe h des Sternenorts G in Beziehung zu setzen mit der Tageszeit t und dessen Deklination δ, denn die Seite PG liegt im Rektaszensionssystem, die Seite ZG im Horizontsystem und die Seite PZ in beiden.
Die halbe Tageslänge ist der Winkelabstand des Südmeridians S vom Untergangspunkt U. Gesucht ist also eine Formel für den Winkel ∢SPG = t, wenn G = U. Bekannt sind im Navigationsdreieck: die Länge des Kreisbogens PZ, das ist der Komplementärwinkel der geografischen Breite φ des Beobachters im Horizontsystems: PZ = 90° - φ. Die Länge der Seite GZ ist der Komplementärwinkel der Höhe h: GZ = 90° - h (im Untergangspunkt wird sie Null sein). Die Länge der Seite GP ist der Komplementärwinkel der Deklination δ: PG = 90° - δ. Der Winkel am Pol, ∢ZPG, ist der gesuchte Stundenwinkel t, und der Winkel am Zenith, ∢PZG = 180° - a (es ist der Ergänzungswinkel zu ∢HZS, dem Azimuth!).
Bekannte Stücke:
- PZ = 90° - φ
- GZ = 90° - h
- GP = 90° - δ
Gesuchtes Stück:
- ∢GPZ = τ
Zur Berechnung der Stücke im Navigationsdreieck verwendet man den Seitencosinussatz im schiefwinkligen sphärischen Dreieck, denn man kennt die drei Seiten (1. Hauptaufgabe):
- cos a = cos b · cos c + sin b · sin c · cos α
Setzt man nun die Stücke ein:
- a = ZG = 90° - h
- b = PZ = 90° - φ
- c = PD = 90° - δ
- α = ∢GPZ = t
erhält man:
- cos (90° - h) = cos (90° - φ) · cos (90° - δ) + sin (90° - h) · sin (90° - φ) · cos t
und mit sin (90° - α) = cos α und cos (90° - α) = sin α
- sin h = sin φ · sin δ + cos h · cos δ ·cos t
Diese Gleichung wird nun aufgelöst nach cos t:
Wenn — bei Sonnenauf- und untergang — h = 0 und sin h = 0 und cos h = 1 sind, vereinfacht sich die Formel zu:
Mit dieser Formel hat die kaiserliche deutsche Marine nach dem Lehrbuch der Navigation von 1906 die Kompassmissweisung bestimmt. Der Winkel t der Untergangsrichtung wurde bestimmt, wenn die Sonne 4 ⁄ 5 ihres Durchmessers über dem Horizont steht. (Wegen der Refraktion der Atmosphäre!)
Die Deklination der Sonne
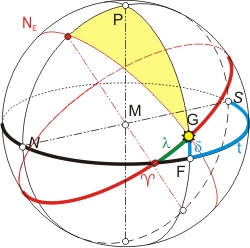 Zur Berechnung der Deklination δ der Sonne muß ein weiteres Koordinatensystem eingeführt werden: das Ekliptikale System. Die Ekliptik ist die Ebene, auf der die Planeten auf Ellipsen um die Sonne kreisen. Die Ebene ist gegenüber dem Himmelsäquator um ε = 23° 27′ geneigt. Ihre Achse durchstößt die Himmelskugel im ekliptikalen Nordpol Nε. (Der Himmelsäquator fällt ja mit dem der Erde zusammen, ebenso die Erdachse mit der Weltachse, die die Himmelskugel im (Nord-)Pol P durchstößt.) Da auch die Mittelpunkte des Äquatorsystems und des Ekliptiksystems zusammen fallen, schneiden sich die beiden Ebenen (die Schnittlinie geht durch den gemeinsamen Mittelpunkt M). Und da die Kugel ja den "Einheitsradius 1" hat, gibt es zwei Schnittpunkte der Schnittlinie mit der Himmelskugel: den Frühlingspunkt ♈ und den Herbstpunkt ♎. Vereinbarungsgemäß zählt man den Winkel auf der Ekliptik von Frühlingspunkt aus entgegen dem Uhrzeigersinn.
Zur Berechnung der Deklination δ der Sonne muß ein weiteres Koordinatensystem eingeführt werden: das Ekliptikale System. Die Ekliptik ist die Ebene, auf der die Planeten auf Ellipsen um die Sonne kreisen. Die Ebene ist gegenüber dem Himmelsäquator um ε = 23° 27′ geneigt. Ihre Achse durchstößt die Himmelskugel im ekliptikalen Nordpol Nε. (Der Himmelsäquator fällt ja mit dem der Erde zusammen, ebenso die Erdachse mit der Weltachse, die die Himmelskugel im (Nord-)Pol P durchstößt.) Da auch die Mittelpunkte des Äquatorsystems und des Ekliptiksystems zusammen fallen, schneiden sich die beiden Ebenen (die Schnittlinie geht durch den gemeinsamen Mittelpunkt M). Und da die Kugel ja den "Einheitsradius 1" hat, gibt es zwei Schnittpunkte der Schnittlinie mit der Himmelskugel: den Frühlingspunkt ♈ und den Herbstpunkt ♎. Vereinbarungsgemäß zählt man den Winkel auf der Ekliptik von Frühlingspunkt aus entgegen dem Uhrzeigersinn.
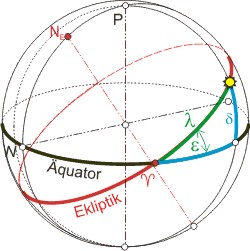
Legt man das Ekliptikalsystem so auf das Äquatorsystem, dass die Mittelpunkte zusammenfallen und der Pol der Ekliptik Nε auf dem Mittagsmeridian liegt, erhällt man die nebenstehende Abbildung. Der Abstand der Sonne G vom Frühlingspunkt ist die ekliptikale Länge λ der Sonne, der Abstand δ die Deklination der Sonne. Sie nimmt von Frühlingspunkt ♈ mit wachsender Länge λ zu bis zum Maximum am Sommersonnenwendepunkt, dann wieder ab bis zum Wintersonnenwendepunkt. Die Berechnung von δ in Anbhängigkeit von λ berechnent man im Dreieck ♈FG, in dem der ∢G♈F = ε und ∢♈FG = 90° (alle Großkreise durch den Pol schneiden alle Meridiane im rechten Winkel). Es gilt Die Seiten eines allgemeinen Dreiecks verhalten sich wie die Sinuswerte der den Seiten gegenüberliegenden Winkel.
Da sin 90° = 1 ergibt die Umformung:
- sin δ = sin λ · sin ε
Oben wurde erwähnt, dass sich die Deklination der Sonne täglich ändert. Das wird an der Abbildung verständlich. Am Frühlingspunkt ♈ ist δ = 0 und die Mittagshöhe der Sonne h☉ = ε und der Tag hat 12 Stunden. (Ist leicht mit den oben abgeleiteten Formeln für δ = 0 zu berechnen.) Nun werden die Tage länger, bis die Sonne den oberen Punkt ihrer Bahn erreicht hat; δ = ε. Dieser Punkt liegt 90° vom ♈-Punkt entfernt. Da die Sonne den ♈-Punkt nach einem vollen Umlauf von 360° wieder erreicht und dabei ein Jahr (zu 365,2472 = 365 d 5 h 56 m (Sonnen-)Tagen) vergangen ist, ist das ¼ Jahr nach dem Frühlingspunktdurchgang. Es entspricht also ein Tag einem Fortschreiten der Sonne auf ihrer ekliptischen Bahn um 0,9856° Mit diesem Wert kann man die Deklination δ für jedes Datum berechnen, wenn man weiss, wann der Durchgang durch den Frühlingspunkt war — leider nicht mit dem Rechenschieber, denn man muss bei einer Genauigkeit von einer Minute mit 4 Stellen nach dem Komma rechnen.
Leider ist die Wirklichkeit nicht so ideal. Man muss den ♈-Punkt jährlich bestimmen. Im Jahr 2014 war der Zeitpunkt am 20. März um 17:57 h MEZ, und 2021 wird er am 20. März um 10:37 MEZ sein. Die Gründe werden auf Astronomie-Sites ausführlich erklärt.
 Wie Kepler in seinem 2. Gesetz postulierte, bewegt sich die Erde auch nicht mit gleichmäßiger Geschwindigkeit auf einer Kreisbahn um die Sonne. Definiert man den Sonnentag als Zeitdifferenz zwischen zwei Meridiandurchgängen der Sonne, und den Sternentag ebenso bezogen auf Meridiandurchgänge eines Fixsterns, so ist der Sonnentag jahreszeitabhängig kürzer oder läger als der Sternentag. Denn die Erde bewegt sich auf ihrer elliptischen Bahn um die Sonne umso schneller, je näher sie der Sonne steht (2. Keplersches Gesetz). Dies ist leicht zu korrigieren: man führt einen mittleren Sonnentag ein, der dem konstanten Umlauf der Sonne auf der Äquatorebene entspricht. Das reicht dann für die Zeitmessung im täglichen Leben. Nicht aber für die Navigation, denn der wahre Sonnentag kann bis zu ¼ Stunde länger oder kürzer sein als der mittlere. Man muss also einen Parameter zum Ausgleich erfinden. In dem kann man dan komfortabel alle Einflüsse zusammenfassen, die auf die Umlaufgeschwindigkeit der Erde einen Einfluss haben: neben der elliptischen Form auch die Anziehungskräfte der anderen Planeten, des Mondes, etc. Diesen Zeit-Ausgleichsparameter nennt man Zeitgleichung:
Wie Kepler in seinem 2. Gesetz postulierte, bewegt sich die Erde auch nicht mit gleichmäßiger Geschwindigkeit auf einer Kreisbahn um die Sonne. Definiert man den Sonnentag als Zeitdifferenz zwischen zwei Meridiandurchgängen der Sonne, und den Sternentag ebenso bezogen auf Meridiandurchgänge eines Fixsterns, so ist der Sonnentag jahreszeitabhängig kürzer oder läger als der Sternentag. Denn die Erde bewegt sich auf ihrer elliptischen Bahn um die Sonne umso schneller, je näher sie der Sonne steht (2. Keplersches Gesetz). Dies ist leicht zu korrigieren: man führt einen mittleren Sonnentag ein, der dem konstanten Umlauf der Sonne auf der Äquatorebene entspricht. Das reicht dann für die Zeitmessung im täglichen Leben. Nicht aber für die Navigation, denn der wahre Sonnentag kann bis zu ¼ Stunde länger oder kürzer sein als der mittlere. Man muss also einen Parameter zum Ausgleich erfinden. In dem kann man dan komfortabel alle Einflüsse zusammenfassen, die auf die Umlaufgeschwindigkeit der Erde einen Einfluss haben: neben der elliptischen Form auch die Anziehungskräfte der anderen Planeten, des Mondes, etc. Diesen Zeit-Ausgleichsparameter nennt man Zeitgleichung:
- wahre Zeit = mittlere Zeit + Parameter.
Die so korrigierte Zeit benutzt man zur Berechnung des Deklination δ der Sonne.
 Die Deklination δ der Sonne über dem Himmelsäquator kann man mit der oben abgeleiteten Formel sin δ = sin λ · sin ε einfach berechnen. Die Umlaufzeit der Erde um die Sonne (gemessen zwischen den beiden Kulminationen der Sonne an zwei Tagen, die in aufeinander folgenden Jahren das gleiche Datum haben) beträgt 365 Tage 6 h 9 m 9,54 s (365,25636 d). Das entspricht einem Umlaufwinkel von 360°. Pro Grad Fortschritt auf der Bahn braucht die Erde also 1,014601 Tage (1 d 21 m 1,526 s), oder pro Tag legt sie 0,98561° zurück. Wir können also den Ort der Erde für jede Zeit auf ihrer Umlaufbahn durch den Winkel λ beschreiben. Dazu müssen wir nur wissen, wann der Frühlingspunkt ♈ passiert wurde und wieviele Tage seit diesem Zeitpunkt verstrichen sind. Das gelingt mit dem Julianischen Datum, wenn man weiß, wann der Durchgang der Sonne durch den Frühlingspunkt stattfand. Im Jahr 2016 fand das am 20. März um 05:30 h statt. Nun müssen wir zunächst die Julianischen Daten der bürgerlichen ausrechnen. Nehmen wir das Datum, an dem wir λ bestimmen wollen als den 05.08.2016 an, der Sonnenstand soll für 12:00 h UTZ bestimmt werden.
Die Deklination δ der Sonne über dem Himmelsäquator kann man mit der oben abgeleiteten Formel sin δ = sin λ · sin ε einfach berechnen. Die Umlaufzeit der Erde um die Sonne (gemessen zwischen den beiden Kulminationen der Sonne an zwei Tagen, die in aufeinander folgenden Jahren das gleiche Datum haben) beträgt 365 Tage 6 h 9 m 9,54 s (365,25636 d). Das entspricht einem Umlaufwinkel von 360°. Pro Grad Fortschritt auf der Bahn braucht die Erde also 1,014601 Tage (1 d 21 m 1,526 s), oder pro Tag legt sie 0,98561° zurück. Wir können also den Ort der Erde für jede Zeit auf ihrer Umlaufbahn durch den Winkel λ beschreiben. Dazu müssen wir nur wissen, wann der Frühlingspunkt ♈ passiert wurde und wieviele Tage seit diesem Zeitpunkt verstrichen sind. Das gelingt mit dem Julianischen Datum, wenn man weiß, wann der Durchgang der Sonne durch den Frühlingspunkt stattfand. Im Jahr 2016 fand das am 20. März um 05:30 h statt. Nun müssen wir zunächst die Julianischen Daten der bürgerlichen ausrechnen. Nehmen wir das Datum, an dem wir λ bestimmen wollen als den 05.08.2016 an, der Sonnenstand soll für 12:00 h UTZ bestimmt werden.
Die Formel zur Umrechnung des bürgerlichen in das julianische Datum JD lautet:
- JD = J · 365,2422 + (M + 1) · 30,6001 + S + T + UT ⁄ 24 + 1.720.996,5
- dabei ist:
- Monat 1 oder 2 (Januar oder Februar): J = JJJJ - 1 und M = MM + 12
- Monat größer als 2: J = JJJJ, M = MM
- Anzahl der Schalttage S = (ganzzahliger Teil J ⁄ 100) - (ganzzahliger Teil J ⁄ 400)
- T ist das Tagesdatum
| 20.03.2016 05:30 h | 05.08.2016 12:00 h | |
| J | 2016 | 2016 |
| M | 4 | 9 |
| S | 20 - 5 = 15 | 20 - 5 = 15 |
| UT | 5,5 | 12 |
| JD | 2.457.472,4048 | 2.457.610,6761 |
| Diff. | 138,2713 d = 138 d 6 h 30 m 43,2 s ≙ 136,2868° | |
Die Sonne ist auf ihrer Bahn also 136,2868° vom Frühlingspunkt ♈ entfernt.
Zur Berechnung der Höhe δ der Sonne über dem Äquator (Deklination) benutzt man das rechtwinklige sphärische Dreieck mit den Seiten λ und δ und dem Winkel ε. Die Formel lautet:
- sin δ = sin λ · sin ε
Mit dieser Formel berechnet man die Deklinationstabellen. Die Korrektur der Zeitgleichung bringt man beim Julianischen Datum an.
Dieser Rechengang setzt voraus, dass die Schiefe der Ekliptik ε konstant sei. Exakt gilt das nur in begrenzten Zeiträumen, da die Neigung der Erdachse relativ zur Bahnebene vielen Einflüssen unterliegt, die Teils von Planetenkonstellationen, teils von Masseverschiebungen auf der Erde beeinflusst werden (sieh z. B. die Überlegungen zum Milanković-Zyklen).
- Zum Thema gehörende Seiten:
- [sphärische Trigonometrie - Grundlagen]
- [Das rechtwinklige sphärische Dreieck]
- [Das schiefwinklige sphärische Dreieck]
- [Anwendungen der sphärische Trigonometrie] (Orthodrome, Tageslänge, Deklination der Sonne)
- [Anwendungen der sphärische Trigonometrie] (Sonnenhöhe, indischer Kreis)
- [Die Nepersche Regel]
- [Beispielrechnung]
- [Konstruktion mit Projektion der Kugel]